1. 交叉熵损失CrossEntropyLoss

交叉熵损失鼓励模型对同一类别提取相似特征。这可能有助于对Imagenet或cityscape等数据集进行分类或分割，在这些数据集中，相同类别的对象应该具有类似的特征。然而，在图像伪造定位中，由于不同的操作会在被篡改区域留下不同的伪造足迹，因此对数据集中所有被篡改区域提取相似的特征并不是最优的。因此，在没有附加约束的情况下，一个常见的基于交叉熵损失的框架容易对特定的伪造模式进行过拟合，这不利于泛化。

import torch.nn as nn
criterion = nn.CrossEntropyLoss(weight = imbalance_weight)
loss = criterion(pred, tar.long().detach())

最优化的目标是找到一组模型参数 θ，使得交叉熵损失在训练数据上最小化： \[\operatorname*{min}_{\theta}L_{C E}(\theta)=-\frac{1}{N}\sum_{n=1}^{N}\sum_{i=1}^{C}y_{i}^{(n)}\log(p_{i}^{(n)}(\theta))\] 其中 N是训练样本数。

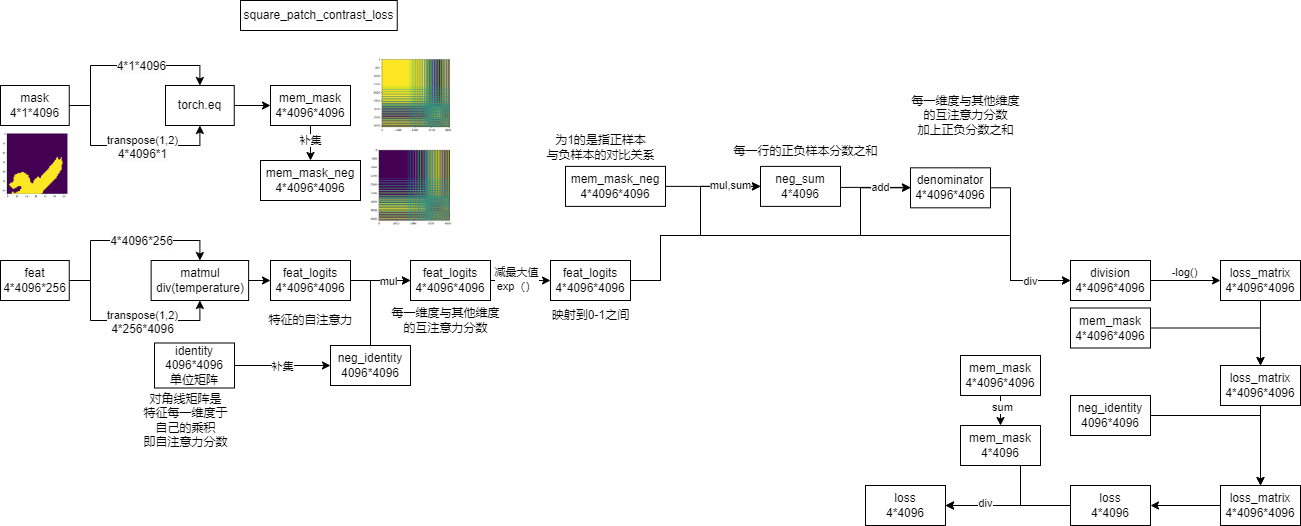
2. 块对比损失PatchContrastLoss

来自于CFL-Net

  我们首先将 $ F∈R^{256×H×W} $ 在空间上划分为k×k个块，从而得到 $ f_iR^{256hw} $ ，其中 $ i{1,2,3…k^2} $ 、 $ h= $ 和 $ w= $ 。然后，我们取每个局部区域中像素嵌入的平均值。从而使每个 $ f_i $ 都变成了 $ R^{256} $ 的形状。以类似的方式，我们将地面真实掩模M划分为k×k个块。Mask在未被篡改区域的值为0，在伪造区域的值为1。我们得到 $ m_iR^{hw} $ ，其中 $ i{1,2,3…k^2} $ 、 $ h= $ 和 $ w= $ 。为了得到每个 $ m_i $ 的标签值，我们计算了h×w个块中的0和1的数量。然后，我们指定块中的最大值为 $ m_i $ 的值。

  然后，我们有了像素嵌入 $ f_i $ 和每个嵌入 $ m_i $ 的相应标签。我们现在得到监督对比损失： \[L_i=\frac{1}{|A_i|}\sum_{k\in A_i}-log(\frac{exp(f_i\cdot k^+/ \tau)}{exp(f_i\cdot k^+/ \tau)+\sum_{k^-}exp(f_i\cdot k^-/ \tau)})\]   其中， $ A_i $ 表示与 $ f_i $ 具有相同标签的所有其他像素嵌入 $ k^+ $ 的集合。类似地， $ k^− $ 是所有与 $ f_i $ 有不同标签的负像素嵌入。损失函数中的所有嵌入都是 $ L_2 $ 归一化的。对于单个图像样本，我们通过对所有嵌入的平均得到最终的对比损失： \[L_{CON}=\frac{1}{k^2}\sum_{i\in k^2}L_i\]

CFL-Net-contrast-loss.drawio

3. InfoNCE对比损失

​  FOCAL 的训练过程如图3 (b)所示：

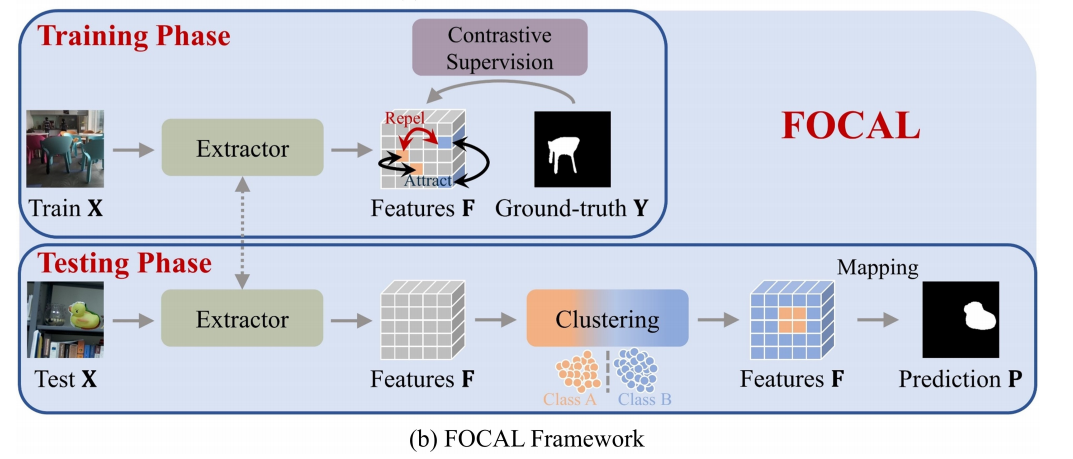
image-20240518144850862

​  一旦我们从给定的输入X中提取高级特征F，我们就通过像素级对比学习直接监督F。地面真实伪造掩模Y自然为我们提供了正和消极类别的索引，使有效的像素级对比学习。正如很快就会更清晰的那样，焦点的对比学习以逐图像的方式进行监督，这与现有的对整个正向小批执行监督的算法[19,6,15,54,56]有很大的不同。

​  具体来说，我们采用了一种改进的InfoNCE损失[16,35]来实现焦点中的对比学习。

​  我们首先通过执行一个扁平化操作来构造一个字典 $ f( ) : { }^{ } ^{ } $ \[f(F) \rightarrow \{ q , k^+_1 , k^+_2 , ..., k^+_J , k^-_1 , k^-_2 , ..., k^-_K \}\] ​  其中， $ { q , k^+_1 , k^+_2 , ..., k^+_J , k^-_1 , k^-_2 , ..., k^-_K } $ 被定义为字典，q是一个编码查询。我们让 $ { q , k^+_1 , k^+_2 , ..., k^+_J } $ 表示属于原始区域的特征（以Y中的0为索引），而 $ { k^-_1 , k^-_2 , ..., k^-_K } $ 表示伪造区域的特征（以Y中的1索引）。

​  在图像伪造检测任务中，伪造或原始区域通常覆盖超过1像素（特征）的区域，这意味着字典中正键J的数量也远远大于1。然后，根据图像伪造任务而定制的改进的信息损失可以计算为 \[{\cal {L}}_{InfoNCE++}=-log \frac { \frac 1 J \sum _{ j \in [1,J] } exp(q \cdot k^+_J / \tau ) } { \sum _{ i \in [1,K] } exp(q \cdot k^+_i / \tau ) }\] ​  其中， $ $ 是一个温度超参数[51]。注意，在原始的InfoNCE loss [16,35]中，字典中只有一个q匹配的正键。在我们改进的InfoNCE损失(2)中，我们通过取q的 $ { k^+_j } $ 的期望，在每个损失计算中涉及所有的正键。这将促进优化过程。

​  需要强调的是，训练阶段的监督是直接在地面真实伪造掩模Y和提取的特征F之间进行的，而没有生成预测的伪造掩模。

​  此外，对于前向小批量中的每一幅图像， $ { \cal {L}} _ { InfoNCE++ } $ 以逐图像的方式（one-by-one）计算，而不是对整个批量进行计算，然后求和计算总体损失。更具体地说，给定一个小批特征 $ {F_1、F_2、···、F_B} $ ，总体对比损失 $ { \cal {L}} _ { ct } $ : \[{\cal {L}}_{ct}=\frac {1} {B} \sum _{b=1} ^{B} ({\cal {L}}_{InfoNCE++}(F_b))\] ​  请注意，在上述（3）式中，没有合并小批特征来计算整体的 $ { \cal {L}}_{InfoNCE++} $ ，避免了训练数据的交叉图像影响。在伪造/原始像素的相对定义的指导下设计的总损失与[5,15,16,32]中的损失有很大的不同，[5,15,16,32]中的损失计算是在批处理级别进行的。

​  为了进一步证明(3)的合理性，我们在图4中绘制了传统的基于批处理和我们的逐图像图像的对比损失曲线。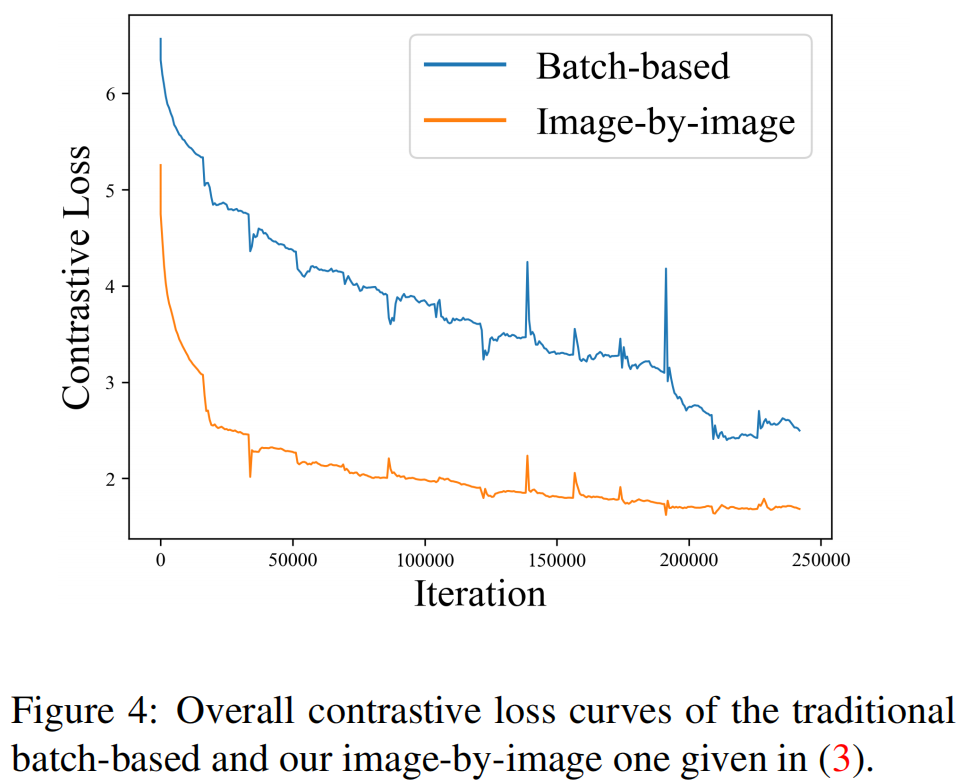
image-20240518153103103

​  可以清楚地看到，损失函数（橙色线）的逐图像设计不仅使收敛速度更快，而且使优化更加稳定。特别是，在蓝线中检测到的高振幅脉冲表明相关的图像中可能存在严重的冲突，例如，类似于图2 (a)和(b)的情况，其中出现冲突的标签。

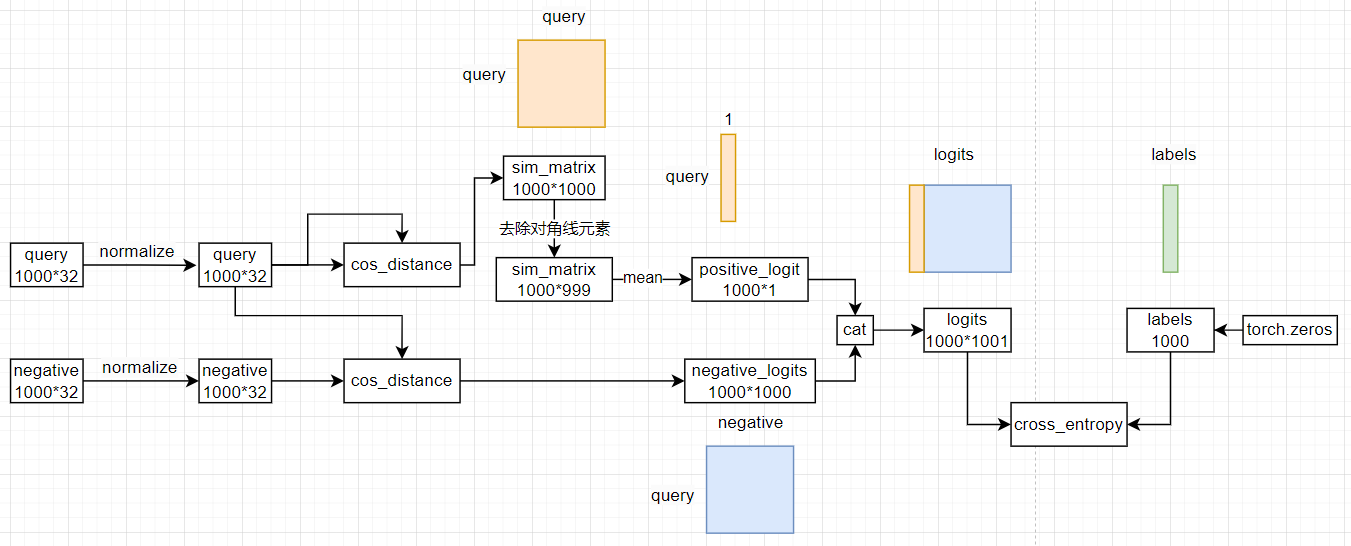
image-20240519102823673

让我们简化一下问题，假设我们只有一个查询样本，并且有3个负样本。

简化场景

  • 查询样本（query）：q
  • 正样本（positive key）：p
  • 负样本（negative keys）：n1, n2, n3

在InfoNCE损失中，我们的目标是让模型学会区分 q 和它的正样本 p，同时推开所有负样本 n1, n2, n3。

构建相似度得分

对于这个例子，我们会计算4个相似度得分：

  1. q 和 p 之间的相似度得分，记作 s_qp
    2. q 和 n1 之间的相似度得分，记作 s_qn1
    3. q 和 n2 之间的相似度得分，记作 s_qn2
    4. q 和 n3 之间的相似度得分，记作 s_qn3

这些相似度得分会组成一个向量 [s_qp, s_qn1, s_qn2, s_qn3]。在这个向量中，s_qp 是我们希望模型最大化得分的位置，因为它代表了查询样本和其对应的正样本之间的相似度。

构建 logits 和 labels

在实际的代码实现中，这个相似度得分向量会被组织成 logits 张量的一部分。对于每个查询样本，logits 的结构如下：

  • 第一个元素是与正样本的相似度得分（即 s_qp）
  • 接下来的元素是与各个负样本的相似度得分（即 s_qn1, s_qn2, s_qn3）

因此，对于上述例子中的单个查询样本，logits 将是一个形状为 [1, 4] 的张量，其中第一个元素对应于正样本的相似度得分。

现在，labels 应该指示出哪个位置是我们期望模型正确分类为目标类别的索引。因为我们希望模型识别出正样本（即 logits 中的第一个元素），所以我们将 labels 设置为0，表示正样本的索引是0。

[s_qp, s_qn1, s_qn2, s_qn3]。在这个向量中，s_qp 是我们希望模型最大化得分的位置。s_qn1、s_qn2、s_qn3 是我们希望模型最小化得分的位置。对应的不是[最大化，最小化，最小化，最小化] ，所有label并不应该是[1，0，0，0]吗?

你的直觉是合理的，但 InfoNCE 损失函数的工作方式稍微不同。InfoNCE 并不是直接最小化负样本的得分，而是通过最大化正样本相对于所有负样本的相对得分来实现对比学习的目标。这可以通过使用 softmax 函数和交叉熵损失来完成。

为什么 labels 是全0

在构建 logits 张量时，我们把正样本的相似度得分放在每个批次元素的第一个位置（索引为0）。因此，对于每一个查询样本而言，logits 的结构如下：

  • 第一个元素是查询样本与它的正样本之间的相似度得分。
  • 后续的元素是查询样本与各个负样本之间的相似度得分。

当我们设置 labels 为全0时，我们实际上是在告诉交叉熵损失函数：“对于每一个查询样本，正样本的索引是0。” 也就是说，我们希望模型能够正确地选择第一个位置上的得分作为最高分。

如何理解 labels

labels 中的0并不意味着最小化或最大化，而是指定了正确的类别索引。在我们的例子中，正确的类别就是正样本，它总是位于 logits 的第一个位置。因此，labels 设置为全0表示我们希望模型将正样本识别为最可能的类别。

交叉熵损失的作用

交叉熵损失会根据 logits 和 labels 来计算实际的损失值。具体来说，它会尝试让 logits 中对应于 labels 指定位置（即正样本的位置）的得分尽可能高，同时其他位置（即负样本的位置）的得分尽可能低。这并不是直接最小化负样本得分，而是在所有候选得分中，使得正样本的得分相对更高。