1. 自编码器（autoencoder）

自编码器（autoencoder）内部有一个隐藏层 h，可以产生编码（code）表示输入。
该网络可以看作由两部分组成：

由函数$h = f ( x )$表示的编码器
生成重构的解码器$r = g(h)$，整体结构如下图所示：

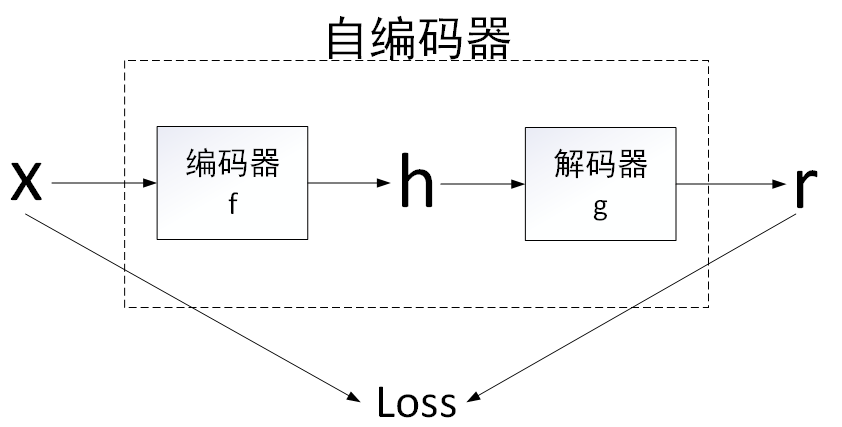
自编码器的一些基本概念

欠完备自编码器：h维度<x维度。

学习欠完备的表示将强制自编码器捕捉训练数据中最显著的特征。“学习欠完备的表示”意味着编码器被设计成只能生成比输入数据更简单、更压缩的表示。举一个简单的例子：
假设你有一堆猫和狗的图片。一个没有任何限制的自编码器可能会尝试记住每张图片的所有细节（毛色、背景等等）。但是，如果我们限制自编码器只能生成非常简化的表示，它就会被迫关注猫和狗最明显的特征，比如猫的尖耳朵和狗的长尾巴，而忽略背景和毛色等次要特征。

过完备自编码器：h维度>=x维度。

过完备则与欠完备相反。“过完备”意味着编码器的表示空间非常大，能够容纳甚至超过输入数据中的所有信息。举一个简单的例子：
假设你有一堆猫和狗的图片。一个过完备自编码器可能会记住每张图片的所有细节，包括背景、毛色、姿态等等。这使得它在训练数据上表现非常好，但在遇到新的猫狗图片时，可能无法很好地识别出它们的共同特征。
在过完备的情况下，可能会出现编码器无法学习到有效信息的情况。这是因为：当编码维数与输入维数相等或更大时，自编码器的表示空间非常大，足以容纳输入数据中的所有信息。在这种情况下，甚至简单的线性编码器和解码器也可以直接将输入复制到输出，而不需要提取任何有用的特征。这意味着自编码器没有被迫去学习数据的分布特征，因为它可以简单地记住所有的数据。这种记忆机制使得模型在训练数据上表现很好，但在面对新数据时可能表现很差，因为它没有学到数据的内在模式或结构。

1 传统自编码器（AE）

AE的网络结构如下：包含三层——输入层、隐藏层、输出层，每一层都是由若干个神经元组成的。

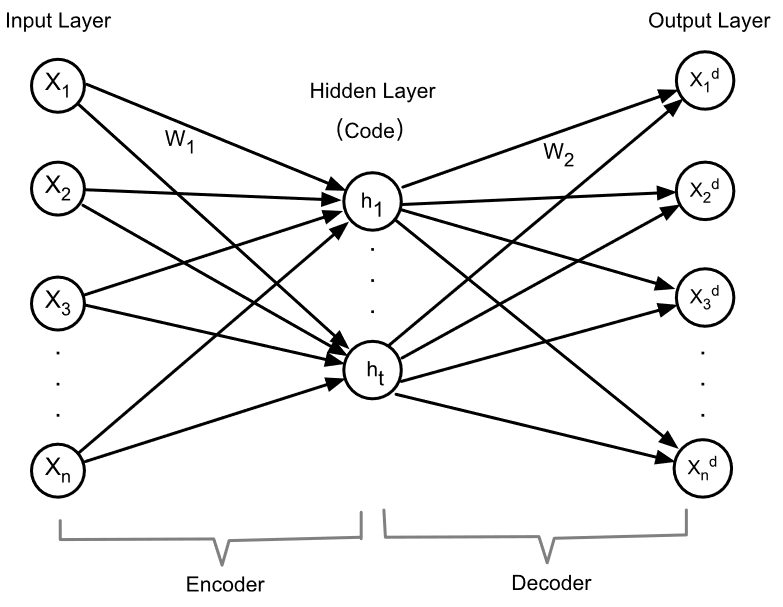
编码：$h=f(x)=f(W_1X+b_1)$
解码：$X_d=g(x)=g(W_2h+b_2)$
损失函数：$J_{AE}\left(\theta\right)=J(X,X^d)=-\sum_{i=1}^n(x_i\log(x_i^d)+(1-x_i)\log(1-x_i^d))$
采用梯度下降法即可进行训练。此外，为了控制权重降低的程度，防止自编码器的过拟合，将在上述损失函数中加入正则化项(也称重量衰减项)，变为正则化自编码器：$J_{\mathrm{ReAE}}(\theta)=J(X,X^d)+\lambda\parallel W\parallel_2^2$

2 去噪自编码器（DAE）

DAE的网络结构如下，AE的目的是求h，但它没有使用h的真实值来训练，所以是无监督的。而DAE的目的是使得网络能够进行去噪，目的是求X，但它用到了X真实值做loss，所以他是监督学习。

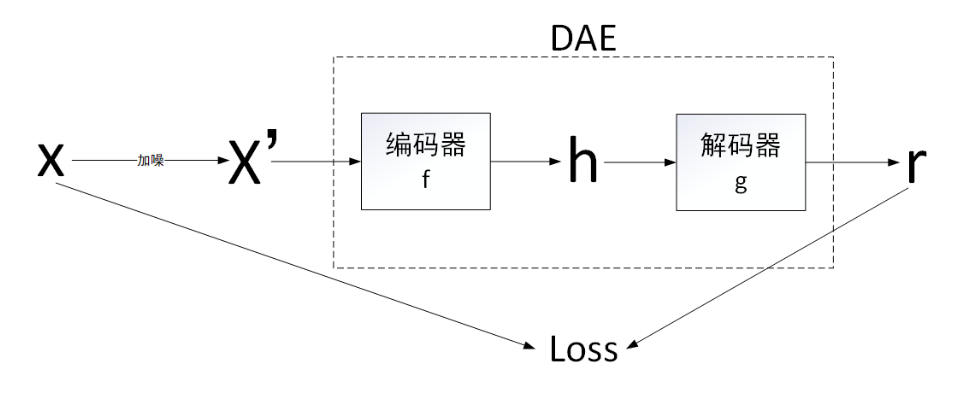
DAE的动机是主动给X加噪，使得网络带有去噪的能力。但是在每次网络训练之前，人为地在干净的输入信号中加入噪声，增加了模型的处理时间。而且，如果加入过多的噪声，会导致输入样本的严重失真，从而降低算法的性能。

3 稀疏自编码器（SAE）

稀疏自编码器利用了X的先验信息，这个先验信息就是X的稀疏度。它的网络结构和AE没有什么区别，但是损失函数变了，添加了一项KL散度，是编码后h的稀疏度和真实稀疏度之间的散度。$J_{SAE}(\theta)=J(X,X^d)+\beta\sum_{j=1}^tKL(\rho\parallel\hat{\rho}_j)$其中$\beta$是控制稀疏惩罚的系数，为0~1。
首先定义每个隐藏单元j jj的平均激活值$\hat{\rho}_j$ : $\hat{\rho}_j=\frac1n\sum_{i=1}^nh_j\left(x_i\right)$
其中，n是训练样本数量，$h_j{(x_i)}$第i个样本对于隐藏单元j的激活值。
然后定义目标稀疏度$\rho$,这是希望隐藏单元的平均激活值。例如，如果$\rho$较小(如0.05),则希望大多数隐藏单元在任何给定时间都不活跃。
最后，将稀疏惩罚项加入到损失函数中，使用KL散度来衡量目标稀疏度和实际稀疏度之间的差异：$\mathrm{KL}(\rho||\hat{\rho}_j)=\rho\log\frac{\rho}{\hat{\rho}_j}+(1-\rho)\log\frac{1-\rho}{1-\hat{\rho}_j}$
稀疏惩罚项的总和是所有隐藏单元的KL散度之和：$ _{j=1}^{t}(||)$<br/>&emsp;&emsp;KL散度是描述两个分布之间差异的指标，KL散度越小，分布越接近，具体公式如下：$KL(_j)=+(1-)$

4 变分自编码器（VAE）

首先说明变分自编码器的总体意义：VAE是在自编码器基础上结合了变分贝叶斯推断的方法，旨在学习数据的隐含结构，并能够生成新的、类似于训练数据的样本。可以说VAE的主要目的是生成新的数据。VAE通过显式地建模潜在变量的概率分布，使得潜在空间结构更加明确和可解释，最终能生成新样本。这在生成对抗网络（GAN）出现之前是一个重要的进展。
下面介绍VAE的主要做法：
VAE的整体网络结构简图如下：

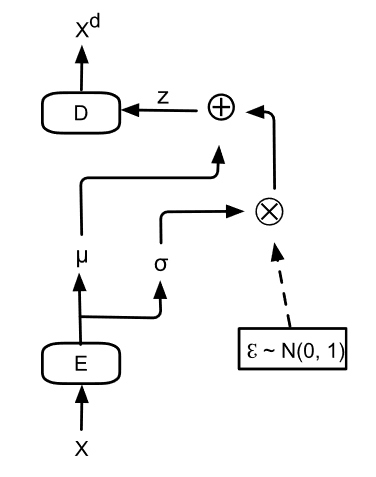
针对一个输入 $x_i$（比如一个样本就是一张图像），网络结构如下（下图中的$\mu_{i}^{\prime}$就是输出的$X^d$ ）：

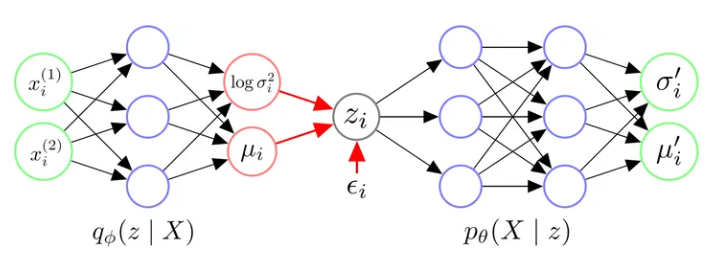
总结一下VAE的架构：

我们首先给Encoder输入一个数据点$x_i$,通过神经网络，我们得到隐变量$z$服从的近似后验分布$q_\phi(z\mid x_i)$的参数。我们往往认为后验分布是一个各维度独立的高斯分布，因此令Encoder输出$z\mid x_i$服从的高斯分布的参数$\sigma_i^2$和$\mu_i$即可。
> 2. 有了$z\mid x_i$分布的参数$\sigma_i^2$和$\mu_i$后，我们从对应的高斯分布中采样出一个$z_i$,这个$z_i$应当代表与$x_i$相似的一类样本。
> 3. 我们令Decoder拟合似然的分布$p_\theta(X\mid z_i)$。喂给Decoder一个$z_i$,它应当返回$X\mid z_i$服从的分布的参数。我们往往认为似然也服从一个各维度独立的高斯分布，因此令Decoder输出$X\mid z_i$服从的高斯分布的参数$\sigma_i^{\prime2}$和$\mu_i^{\prime}$即可。
> 4. 在得到$X\mid z_i$的分布的参数后，理论上我们需要从这个分布中进行采样，来生成可能的数据点$x_{i}$。

上述第四点中值得注意的是，在大部分实现中，人们往往不进行采样，而是直接将模型输出的$\mu_i^{\prime}$当作是给定$z_i$生成的数据点$x_i$ 。
除此之外，人们也往往认为$p_\theta(X\mid z_i)$是一个固定方差的各维度独立的多元高斯分布，即$p_\theta(X\mid z_i)=\mathcal{N}(X\mid\mu_i^{\prime}(z_i;\theta),\sigma^{\prime2}*I)$,其中$\sigma^{\prime2}$是一个人为给定的超参数。这意味着我们实际中并不真的让模型输出$\sigma_i^{\prime2}$,模型只要输出$\mu_i^{\prime}$就行了。
具体公式推导参考上面的那篇博客，下面是对博客推导思想的简单总结：

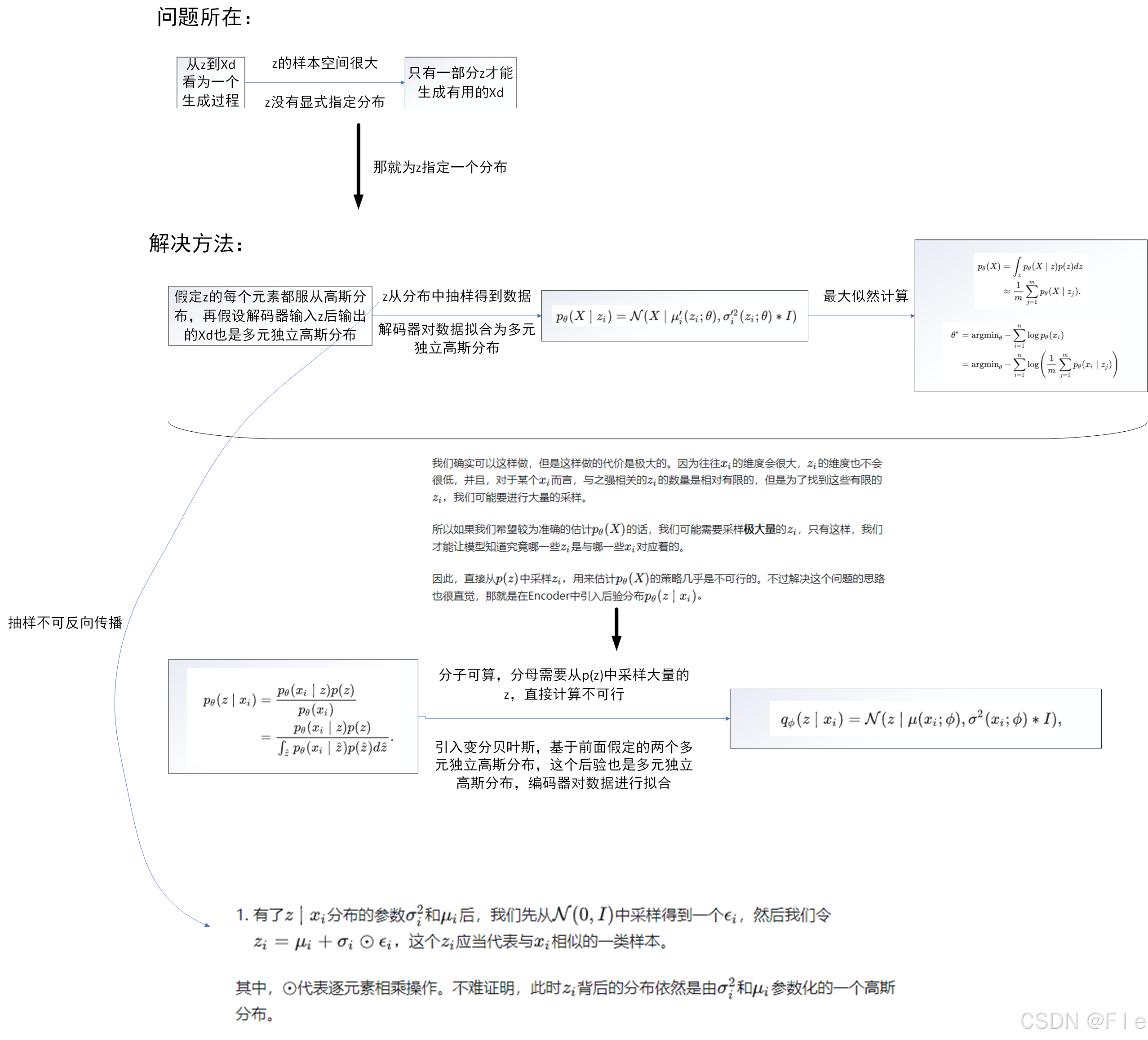
为了更好理解，还是直接博客的代码吧：

# -*- coding: utf-8 -*-

"""
Created on January 28, 2021

@author: Siqi Miao
"""

import os
from tqdm import tqdm
os.environ["KMP_DUPLICATE_LIB_OK"] = "TRUE"

import torch
import torch.nn as nn

from torchvision import transforms
from torchvision.utils import save_image
from torchvision.datasets import MNIST


class VAE(nn.Module):

    def __init__(self, in_features, latent_size, y_size=0):
        super(VAE, self).__init__()

        self.latent_size = latent_size

        self.encoder_forward = nn.Sequential(
            nn.Linear(in_features + y_size, in_features),
            nn.LeakyReLU(),
            nn.Linear(in_features, in_features),
            nn.LeakyReLU(),
            nn.Linear(in_features, self.latent_size * 2)  # latent_size表示潜变量的个数，每一个变量有均值和方差两个数值
        )

        self.decoder_forward = nn.Sequential(
            nn.Linear(self.latent_size + y_size, in_features), # 解码器输入的时候只需要输入编码器输出的潜在变量的均值
            nn.LeakyReLU(),
            nn.Linear(in_features, in_features),
            nn.LeakyReLU(),
            nn.Linear(in_features, in_features),
            nn.Sigmoid()
        )

    def encoder(self, X):
        out = self.encoder_forward(X)
        mu = out[:, :self.latent_size] # 前latent_size个数据是均值
        log_var = out[:, self.latent_size:] # 后latent_size个数据是log(方差)
        return mu, log_var

    def decoder(self, z):
        mu_prime = self.decoder_forward(z)
        return mu_prime

    def reparameterization(self, mu, log_var):  # Reparameterization Trick
        epsilon = torch.randn_like(log_var) # 产生和log_var维度一样的高斯分布数据
        z = mu + epsilon * torch.sqrt(log_var.exp()) # log_var.exp()=var，sqrt(var)就是sigema
        return z

    def loss(self, X, mu_prime, mu, log_var): # mu_prime编码器的输出；mu潜变量的均值，也就是潜变量的值了；log_var潜变量的log(方差)
        # reconstruction_loss = F.mse_loss(mu_prime, X, reduction='mean') is wrong!
        #print(mu_prime.shape) # [1024,784]
        #print(mu.shape) # [1024,64]
        #print(log_var.shape) # [1024,64]
        # torch.square 是一个用于计算张量中每个元素的平方的函数。这个函数返回一个新的张量，其中包含原始张量中每个元素的平方值
        reconstruction_loss = torch.mean(torch.square(X - mu_prime).sum(dim=1)) # sum(dim=1)表示对列求和，torch.mean就相当于是对1024个样本求均值了，也就是公式里的1/n

        latent_loss = torch.mean(0.5 * (log_var.exp() + torch.square(mu) - log_var).sum(dim=1)) # sum(dim=1)表示对潜变量求和，torch.mean相当于是对1024个样本求均值
        return reconstruction_loss + latent_loss

    def forward(self, X, *args, **kwargs):
        mu, log_var = self.encoder(X)
        z = self.reparameterization(mu, log_var)
        mu_prime = self.decoder(z)
        return mu_prime, mu, log_var


class CVAE(VAE): # 继承VAE类，所以可以使用VAE的编码和解码器

    def __init__(self, in_features, latent_size, y_size):
        super(CVAE, self).__init__(in_features, latent_size, y_size)

    def forward(self, X, y=None, *args, **kwargs):
        y = y.to(next(self.parameters()).device)
        #print(y.shape) # [1024]
        X_given_Y = torch.cat((X, y.unsqueeze(1)), dim=1) 
        #print(X_given_Y.shape) # [1024,785]
        
        mu, log_var = self.encoder(X_given_Y)
        z = self.reparameterization(mu, log_var)
        z_given_Y = torch.cat((z, y.unsqueeze(1)), dim=1)

        mu_prime_given_Y = self.decoder(z_given_Y)
        return mu_prime_given_Y, mu, log_var


def train(model, optimizer, data_loader, device, name='VAE'):
    model.train()

    total_loss = 0
    pbar = tqdm(data_loader)
    for X, y in pbar:
        #print(X.shape) # [1024,1,28,28]
        #print(y.shape) # [1024]
        batch_size = X.shape[0]
        X = X.view(batch_size, -1).to(device)
        #print(X.shape) # [1024,784]
        model.zero_grad() #将模型中所有参数的梯度缓存清零。在进行反向传播计算梯度之前，必须先将之前计算的梯度清零。这是因为在 PyTorch 中，梯度是累积的。

        if name == 'VAE':
            mu_prime, mu, log_var = model(X)
        else:
            mu_prime, mu, log_var = model(X, y)

        loss = model.loss(X.view(batch_size, -1), mu_prime, mu, log_var)
        loss.backward()
        optimizer.step()

        total_loss += loss.item()
        pbar.set_description('Loss: {loss:.4f}'.format(loss=loss.item()))

    return total_loss / len(data_loader)


@torch.no_grad()
def save_res(vae, cvae, data, latent_size, device):
    num_classes = len(data.classes)

    # raw samples from dataset
    out = [] # 用于存储每个类别的图像
    for i in range(num_classes): 
        # 提取类别为 i 的图像
        img = data.data[torch.where(data.targets == i)[0][:num_classes]]
        out.append(img)
    out = torch.stack(out).transpose(0, 1).reshape(-1, 1, 28, 28) # 将图像堆叠在一起，并转置维度以便于保存
    save_image(out.float(), './img/raw_samples.png', nrow=num_classes, normalize=True) # 100张图像

    # samples generated by vanilla VAE
    z = torch.randn(num_classes ** 2, latent_size).to(device)
    # print(z.shape) # [100,64]
    out = vae.decoder(z)
    save_image(out.view(-1, 1, 28, 28), './img/vae_samples.png', nrow=num_classes)

    # sample generated by CVAE
    z = torch.randn(num_classes ** 2, latent_size).to(device)
    y = torch.arange(num_classes).repeat(num_classes).to(device)
    z_given_Y = torch.cat((z, y.unsqueeze(1)), dim=1)
    out = cvae.decoder(z_given_Y)
    save_image(out.view(-1, 1, 28, 28), './img/cvae_samples.png', nrow=num_classes)


def main():
    device = 'cuda' if torch.cuda.is_available() else 'cpu'
    device = torch.device(device)

    batch_size = 256 * 4
    epochs = 50
    latent_size = 64
    in_features = 28 * 28
    lr = 0.001

    data = MNIST('./dataset/', download=True, transform=transforms.ToTensor())
    data_loader = torch.utils.data.DataLoader(data, batch_size=batch_size, shuffle=True)

    # train VAE
    vae = VAE(in_features, latent_size).to(device)
    optimizer = torch.optim.AdamW(vae.parameters(), lr=lr)

    print('Start Training VAE...')
    for epoch in range(1, 1 + epochs):
        loss = train(vae, optimizer, data_loader, device, name='VAE')
        print("Epochs: {epoch}, AvgLoss: {loss:.4f}".format(epoch=epoch, loss=loss))
    print('Training for VAE has been done.')

    # train VCAE
    cvae = CVAE(in_features, latent_size, y_size=1).to(device)
    optimizer = torch.optim.AdamW(cvae.parameters(), lr=lr)

    print('Start Training CVAE...')
    for epoch in range(1, 1 + epochs):
        loss = train(cvae, optimizer, data_loader, device, name='CVAE')
        print("Epochs: {epoch}, AvgLoss: {loss:.4f}".format(epoch=epoch, loss=loss))
    print('Training for CVAE has been done.')

    save_res(vae, cvae, data, latent_size, device)


if __name__ == '__main__':
    main()

VAE的变种：条件变分自编码器（CVAE）
传统的VAE可以近似地生成输入数据，但不能定向地生成特定类型的数据。为解决这一问题，将数据x和x的部分标签( y )输入到CVAE的编码器部分。这样就会生成指定类别的数据。CVAE的结构与VAE相似，因此CVAE的计算方法和优化方法与VAE一致。由于在输入中存在一些标签Y，CVAE成为一种半监督学习形式。
参考资料：
[1]《Deep Learning》
[2] Li P, Pei Y, Li J. A comprehensive survey on design and application of autoencoder in deep learning[J]. Applied Soft Computing, 2023, 138: 110176.
[3] 机器学习方法—优雅的模型（一）：变分自编码器（VAE） - 知乎 (zhihu.com)
[4] 自编码器（autoencoder）-CSDN博客