Circle Loss: A Unified Perspective of Pair Similarity Optimization

摘要

本文提出了一种关于深度特征学习的对相似度优化的视点，旨在使类内相似度最大化，类间相似度最小。我们发现了大多数的损失函数，包括triplet损失和softmax交叉熵损失，将 $ s_n $ 和 $ s_p $ 嵌入到相似度对中，并寻求减少 $ (s_n−s_p) $ 。这种优化方式是不灵活的，因为每个相似度得分的惩罚强度被限制为相等。我们的直觉是，如果一个相似度得分远远偏离了最优值，就应该强调它。为此，我们简单地重新加权每个相似度，以突出较少优化的相似度分数。它造就了一个Circle损失，由于它的圆形决策边界而命名。Circle损失对于两种基本的深度特征学习范式有一个统一的范式，即使用类级标签和成对标签进行学习。在分析上，我们表明，与损失函数优化 $ (s_n−s_p) $ 相比，Circle损失提供了一种更灵活的对收敛目标更明确的优化方法。通过实验，我们证明了Circle损失在各种深度特征学习任务中的优越性。在人脸识别、人的再识别以及几个细粒度的图像检索数据集上，所取得的性能与现有的技术水平相当。

1.介绍

本文对两种基本的深度特征学习范式进行了相似性优化分析，即从具有类级标签的数据和具有成对标签的数据中进行学习。前者采用分类损失函数（例如，软最大交叉熵损失[25,16,36]）来优化样本和权向量之间的相似性。后者利用一个度量损失函数（例如，三联体损失[9,22]）来优化样本之间的相似性。在我们的解释中，这两种学习方法之间没有内在的区别。它们都寻求最小化类间相似度 $ s_n $ ，也寻求最大化类内相似度 $ s_p $ 。
从这个角度来看，我们发现许多流行的损失函数（例如，triplet损失[9,22]，softmax交叉熵损失及其变体[25,16,36,29,32,2]）具有相似的优化模式。它们都将 $ s_n $ 和 $ s_p $ 嵌入到相似度对中，并寻求减少 $ (s_n−s_p) $ 。在 $ (s_n−s_p) $ 中，增加 $ s_p $ 相当于减少 $ s_n $ 。我们认为这种对称优化方式容易出现以下两个问题。

缺乏进行优化的灵活性。在 $ s_n $ 和 $ s_p $ 上的惩罚强度被限制为相等。给定指定的损失函数，关于 $ s_n $ 和 $ s_p $ 的梯度具有相同的振幅（详见第2节）。在某些角落的情况下，例如， $ s_p $ 很小，并且 $ s_n $ 已经接近0（图1(a)中的“a”），它继续以较大的梯度惩罚 $ s_n $ 。它是低效的和非理性的。

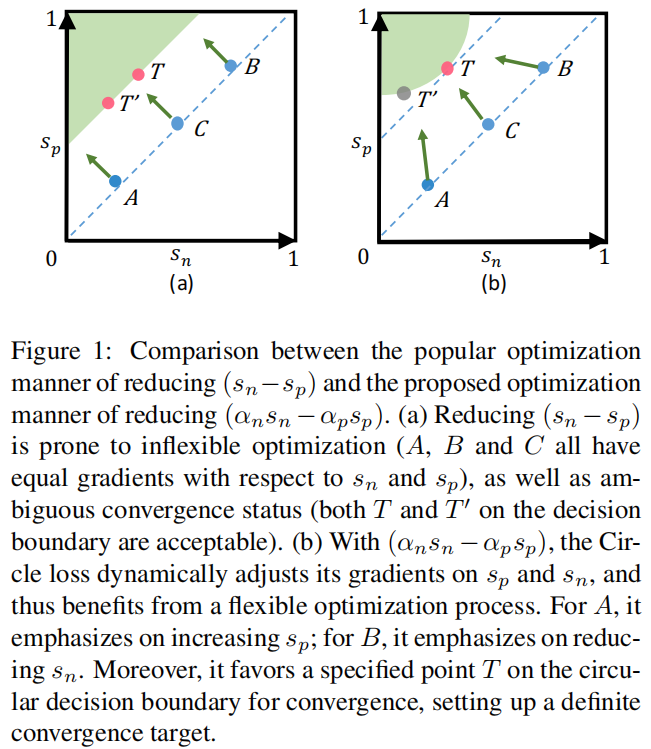
图1：流行的还原优化方式 $ (s_n−s_p) $ 与所提出的还原优化方式 $ (_ns_n−_ps_p) $ 的比较。
(a)还原 $ (s_n−s_p) $ 容易进行不灵活的优化（A、B和C相对于 $ s_n $ 和 $ s_p $ 都有相等的梯度），以及模糊的收敛状态（在决策边界上的T和T0都是可以接受的）。
(b) 在 $ (_ns_n−_ps_p) $ 下，Circle损失动态调整其对 $ s_n $ 和 $ s_p $ 的梯度，从而受益于一个灵活的优化过程。对于A，它强调增加 $ s_p $ ；对于B，它强调减少 $ s_n $ 。此外，它有利于圆形决策边界上的指定点T收敛，建立一个确定的收敛目标。

模糊的收敛状态。优化 $ (s_n−s_p) $ 通常会导致 $ s_n−s_p=m $ （m为边际）的决策边界。这个决策边界允许模糊性（例如，图1(a)中的“ $ T $ ”和“ $ T^{} $ ”）来收敛。例如，有 $ {s_{n},s_{p}}={0.2,0.5} $ ，而 $ T^{} $ 有 $ {s_{n}^{},s_{p}{}}={0.4,0.7} $ 。它们都获得了边际m = 0.3。但是，通过相互比较，我们发现 $ s_{n}^{} $ 和 $ s_{p} $ 之间的差距只有0.1。因此，模糊收敛影响了特征空间的可分性。

有了这些见解，我们就有了一种直觉，即不同的相似性得分应该有不同的惩罚强度。如果一个相似度得分偏离最优值，它应该受到很强的惩罚。否则，如果一个相似度得分已经接近最优值，那么它就应该进行轻微的优化。为此，我们首先将 $ (s_n−s_p) $ 推广为 $ (_ns_n−_ps_p) $ ，其中 $ _n $ 和 $ _p $ 是独立的加权因子，允许 $ s_n $ 和 $ s_p $ 在不同的速度学习。相似度得分偏离最优值越远，加权因子就会越大。这样的优化结果是决策边界 $ _ns_n−_ps_p=m $ ，在 $ (s_n,s_p) $ 空间中产生一个圆的形状，因此我们将所提出的损失函数命名为Circle损失。
由于简单，Circle损失本质上从以下三个方面重塑了深度特征学习的特征：
首先，这是一个统一的损失函数。从统一相似对优化的角度出发，我们提出了两种基本学习范式的类级标签和成对标签学习。
第二，灵活的优化。在训练过程中，反向传播到 $ s_n(s_p) $ 的梯度将被 $ _n(_p) $ 放大。那些弱优化的相似性得分将有更大的权重因子，并因此得到更大的梯度。如图1 (b)所示，对A、B、C的优化是不同的。
第三，有明确的收敛状态。在圆形决策边界上，Circle损失倾向于指定的收敛状态（图1(b)中的“T”），如第3.3节所示。相应地，它建立了一个明确的优化目标，有利于可分性。
本文的主要贡献总结如下：

我们提出了Circle损失，一个简单的损失函数的深度特征学习。通过在监督下对每个相似度得分进行重新加权，有利于优化灵活、确定收敛目标的深度特征学习。
我们提出的Circle损失与兼容性的类级标签和成对的标签。略有修改下，Circle损失将退化为triplet损失或softmax交叉熵损失。
我们对各种深度特征学习任务进行了广泛的实验，如人脸识别、人的再识别、汽车图像检索等。在所有这些任务中，我们证明了Circle损失的优越性与性能与现有的技术相当。

2.统一的视角

深度特征学习的目的是最大化类内相似性 $ s_p $ ，以及减少类间相似性 $ s_n $ 。例如，在余弦相似度度量下，我们期望 $ s_{p} $ 和 $ s_{n} $ 。
为此，使用类级标签学习和使用成对标签学习是两种基本范式。它们通常被认为是分开的，彼此之间的w.r.t与损失函数显著不同。给定类级标签，第一个基本上学习将每个训练样本分类为目标类，例如分类损失。L2-Softmax[21]，Large-margin Softmax[15]，Angular Softmax[16]，NormFace[30]，AMSoftmax[29]，CosFace[32]，ArcFace[2]。这些方法也被称为基于代理的学习，因为它们优化了样本和代表每个类的一组代理之间的相似性。相比之下，给定成对标签，第二个直接学习特征空间中的成对相似性（即样本之间的相似性），因此不需要代理，例如，约束损失[5,1]，三联体损失[9,22]，提升结构损失[19]，n对损失[24]，直方图损失[27]，角损失[33]，基于边际损失[38]，多相似性损失[34]等。
本文从单一的角度来看待这两种学习方法，不偏好基于代理的相似性或基于成对的相似性。给定特征空间中的一个样本x，假设有K个类内相似度得分，L个类间相似度得分。我们将这些相似度得分分别表示为 $ {s_{p}^{i}}(i=1,2, ,K) $ 和 $ {s_{n}^{j}}(j=1,2,,L) $ 。
为了最小化每个 $ s_{n}^{j} $ 以及最大化 $ s_{p}^{i} $ ， $ (i {1,2, ,,K},j {1,2, ,,L}) $ ，我们提出了一个统一的损失函数： \[\begin{aligned}{\mathcal{L}}_{u n i} &= \log\left[1+\sum_{i=1}^{K}\sum_{j=1}^{L}\exp(\gamma(s_{n}^{j}-s_{p}^{i}+m))\right]\\ &=\mathrm{log}\left[1+\sum_{j=1}^{L}\exp(\gamma(s_{n}^{j}+m))\sum_{i=1}^{K}\exp(\gamma(-s_{p}^{i}))\right]\end{aligned}\] 其中 $ $ 是一个尺度因子， $ m $ 是一个更好的相似性分离的边际。
等式1是直观的。它遍历每一个相似度对来减少 $ (s_{n}^{j}-s_{p}{i}) $ 。我们注意到，通过轻微的修改，它可以退化为三联体损失或分类损失。

给定类级标签，我们计算了分类层中 $ x $ 和权重向量 $ w_{i} (i=1,2, , N) $ （N是训练类别数）之间的相似性得分。
具体来说，我们通过： $ s_{n}^{j}=w_{j}{}{x}/{(}||w_{j}|||x||{)} $ （ $ w_{j} $ 是第j个非目标权重向量）得到（N−1）类间相似性得分。此外，我们得到了一个单一的类内相似性评分（省略了上标） $ s_{p};=;w_{y}^{}x/(||w_{y}|||x||) $ 。有了这些先决条件，等式1退化为AM-Softmax [29,32]，这是Softmax损失的一个重要变体（即，Softmax交叉熵损失）： \[\begin{aligned}{\mathcal{L}}_{a m}&=\log\left[1+\sum_{j=1}^{N-1}\exp(\gamma(s_{n}^{j}+m))\exp(-\gamma s_{p})\right]\\&=-\log\frac{\exp(\gamma(s_{p}-m))}{\exp(\gamma(s_{p}-m))+\sum_{j=1}^{N}\exp(\gamma s_{n}^{j})}\end{aligned}\] 此外，当 $ m=0 $ ，等式2进一步退化为Normface[30]。如果将内积替换余弦相似度，并且设置 $ $ ，它最终退化为Softmax损失。

给定成对的标签，在小批量中，我们计算x和其他特征之间的相似性得分。具体来说， $ s_{n}^{j}=(x_{n}{j})^{}x/(||x_{n}{j}|||x||) $ （ $ x_{n}^{j} $ 是负样本集 $ {} $ 中的第j个样本）和 $ s_{p}^{j}=(x_{p}{j})^{}x/(||x_{p}{j}|||x||) $ （ $ x_{p}^{j} $ 是正样本集 $ {} $ 中的第i个样本）。相应地， $ K=|P|,,L=|{}| $ 。等式1与硬挖掘[22,8]退化为triplet损失： \[\begin{aligned}{\mathcal{L}}_{t r i}&=\operatorname*{lim}_{\gamma\to+\infty}{\frac{1}{\gamma}}{\mathcal{L}}_{u n i}\\&=\operatorname*{lim}_{\gamma\to+\infty}\frac{1}{\gamma}\log\left[1+\sum_{i=1}^{K}\sum_{j=1}^{L}\exp(\gamma(s_{n}^{j}-s_{p}^{i}+m))\right]\\&=\operatorname*{max}\left[s_{n}^{j}-s_{p}^{i}+m\right]_{+}\end{aligned}\] 具体来说，我们注意到在等式3中，“ $ ({}) $ ”操作采用Lifted-Structure损失[19]， N-pair损失[24]，多相似性损失[34]等，在样品之间进行“软化”硬挖掘。 $ $ 的扩大逐渐增强了挖掘强度，当 $ +$ 时，导致了[22,8]的典型硬挖掘。

梯度分析。等式2和等式3显示了triplet损失，Softmax损失及其几个变体可以被解释为等式1的特定情况。换句话说，它们都在优化 $ (s_n−s_p) $ 。

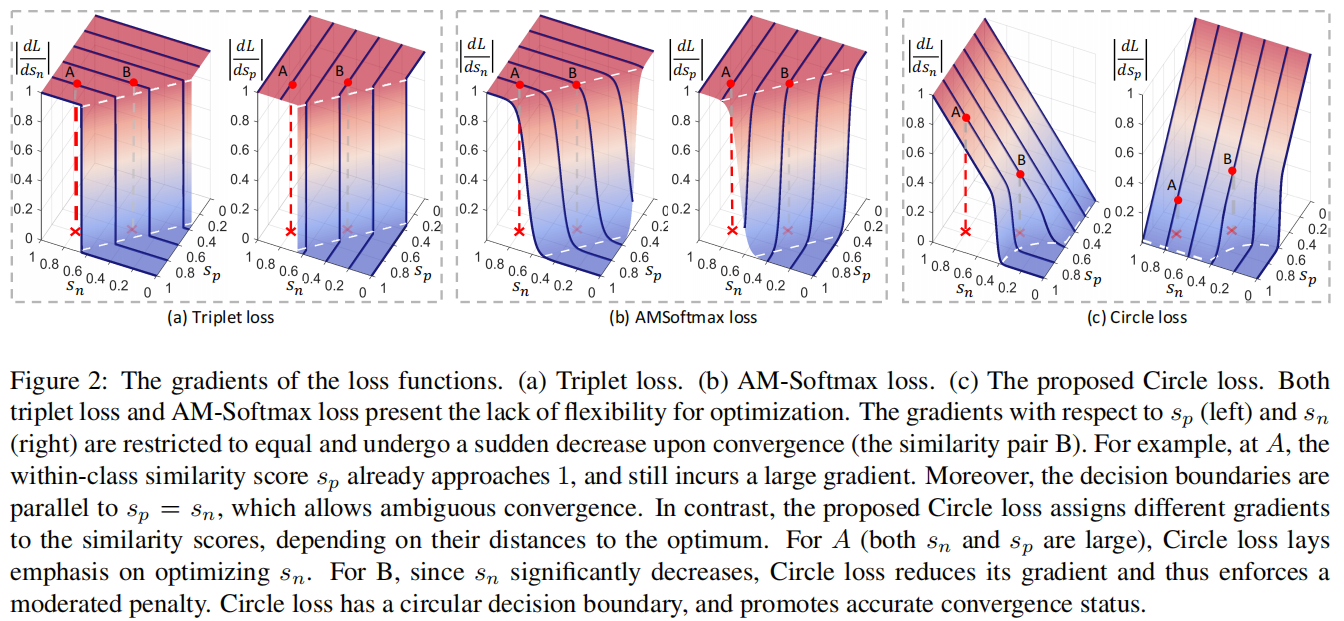
图2：损失函数的梯度。(a)triplet的损失。(b) AM-Softmax损失。(c)提出的Circle损失。triplet损失和AM-Softmax损失都缺乏优化的灵活性。 $ s_p $ （左）和 $ s_n $ （右）的梯度被限制为相等，并在收敛时突然下降(相似对B）。例如，在A处，类内相似度评分 $ s_p $ 已经接近1，并且仍然有一个很大的梯度。此外，决策边界与 $ s_p=s_n $ 平行，允许模糊收敛。相比之下，提出的Circle损失分配不同的梯度，取决于它们到最优的距离。对于A（ $ s_n $ 和 $ s_p $ 都很大），Circle损失的重点是优化 $ s_n $ 。对于B，由于 $ s_n $ 显著减少，Circle损失减少了它的梯度，从而加强了一个温和的惩罚。Circle损失具有一个圆形的决策边界，并促进了准确的收敛状态。

在只有一个 $ s_n $ 和 $ s_p $ 的小场景下，我们在图2 (a)和(b)中可视化了中的triplet损失和AM-Softmax损失的梯度，从中我们得出以下观察结果：

首先，在损失达到其决策边界之前（梯度消失之前），相对于 $ s_p $ 和 $ s_n $ 的梯度是相同的。状态A具有 $ {s_{n},s_{p}} = {0.8,0.8} $ ，表示良好的类内紧致性。然而，A相对于 $ s_p $ 仍然有较大的梯度。它导致了在优化过程中缺乏灵活性。
第二，梯度在收敛前保持（大致）不变，并在收敛时发生突然的下降。状态B更接近决策边界，并且比A优化得更好。然而，损失函数（triplet损失和AMSoftmax损失）对A和B施加近似相等的惩罚。这是缺乏灵活性的另一个证据。
第三，决策边界（白色虚线）平行于 $ s_{n}-s_{p}=m $ 。该边界上任意两点（如图1中的 $ {} $ 和 $ {}^{} $ ）的相似间隙等于m，因此具有相同的困难。换句话说，损失函数最小化 $ (s_{n}-s_{p}+m) $ 在 $ {} $ 或 $ {}^{} $ 的收敛性上不偏不倚，并且容易出现模糊收敛。关于这个问题的实验证据，请参见第4.6节。

这些问题源于最小化 $ (s_{n}-s_{p}) $ 的优化方式，其中减少 $ s_n $ 相当于增加 $ s_p $ 。在下面的第3节中，我们将把这种优化方式转换为更一般的优化方式，以促进更高的灵活性。

3.一个新的损失函数

3.1.自定速度的加权

我们考虑通过允许每个相似度评分根据当前优化状态以自己的速度学习来增强优化灵活性。我们首先忽略了等式1中的边际项m，并通过以下方式将统一损失函数转换为提出的Circle损失： $$ \[\begin{aligned}{\mathcal{L}}_{c i r c l e}&=\mathrm{log}\left[1+\sum_{i=1}^{K}\sum_{j=1}^{L}\exp{\left({\gamma(\alpha_{n}^{j}s_{n}^{j}-\alpha_{p}^{i}s_{p}^{i}}\right)}\right]\\&=\log\left[1+\sum_{i=1}^{L}\exp(\gamma\alpha_{n}^{j}s_{n}^{j})\sum_{i=1}^{K}\exp(-\gamma\alpha_{p}^{i}s_{p}^{i})\right] \end{aligned}\] \[ &emsp;&emsp;其中 $ \alpha_{n}^{j} $ 和 $ \alpha_{p}^{i} $ 为非负加权因子。<br/>&emsp;&emsp;等式4来源于等式1，通过将 $ (s_{n}^{j}-s_{p}^{i}) $ 推广为 $ (\alpha_{n}^{j}s_{n}^{j}-\alpha_{p}^{i}s_{p}^{i}) $ 。在训练过程中，当反向传播到 $ {s}_{n}^{j}\,(s_{p}^{i}) $ 时，相对于 $ (\alpha_{n}^{j}s_{n}^{j}-\alpha_{p}^{i}s_{p}^{i}) $ 的梯度将与 $ \alpha_{n}^{j}(\alpha_{p}^{i}) $ 相乘。当相似度得分偏离其最优值时（即， $ s^j_n $ 时为 $ O_n $ ， $ s^i_p $ 时为 $ O_p $ ），应得到一个较大的加权因子，以得到较大梯度的有效更新。为此，我们以一种自定速度的方式来定义 $ \alpha_{p}^{i} $ 和 $ \alpha_{n}^{j} $ ： \] \[\begin{cases}\alpha_{p}^{i}=[O_{p}-s_{p}^{i}]_{+},\\\alpha_{n}^{j}=[s_{n}^{j}-{O}_{n}]_{+}\\\end{cases}\]

$$ 其中[·]+为“零截止”操作，以确保 $ {p}^{i} $ 和 $ {n}^{j} $ 为非负值。
讨论。在监督下重新调整余弦相似度是现代分类损失[21,30,29,32,39,40]中常见的做法。传统上，所有的相似性得分都具有相同的尺度因子 $ $ 。当我们将一个分类损失函数中的softmax值看作是一个样本属于某一类的概率时，等量的重新缩放是很自然的。相比之下，Circle损失在重新缩放之前用一个独立的加权因子乘以每个相似度分数。因此，它摆脱了平等的重新缩放的约束，并允许更灵活的优化。除了更好的优化的好处外，这种重新加权（或重新缩放）策略的另一个意义还涉及到潜在的解释。Circle损失放弃了将样本以大概率分类为目标类的解释。相反，它具有相似度对的优化视角，这与两种学习范式相兼容。

3.2.类内和类间的边际

在损失函数优化 $ (s_{n}-s_{p}) $ 中，添加一个边际 $ m $ 加强了优化[15,16,29,32]。由于 $ s_{n} $ 和 $ -s_{p} $ 处于对称位置， $ s_{n} $ 的正边际等于于 $ s_{p} $ 的负边际。因此，它只需要一个单一的边际 $ m $ 。在Circle损失中， $ s_n $ 和 $ s_p $ 处于不对称位置。当然，它需要 $ s_n $ 和 $ s_p $ 各自的边际，其公式如下： \[\mathcal{L}_{c i r c l e}=\log\left[1+\sum_{i=1}^{L}\exp(\gamma\alpha_{n}^{j}(s_{n}^{j}-\Delta_{n}))\sum_{i=1}^{K}\exp(-\gamma\alpha_{p}^{i}(s_{p}^{i}-\Delta_{p}))\right]\] 其中 $ {n} $ 和 $ {p} $ 分别为类间和类内的边距。
基本上，等式6中的Circle损失期望 $ {s}{p}^{{i}{p} $ 和 $ {s}{n}}{j}{n} $ 。通过推导决策边界，进一步分析了 $ {n} $ 和 $ {p} $ 的设置。为简单起见，我们考虑了二值分类的情况，其中决策边界是通过 $ {n}(s{n}-{n})-{p}(s_{p}-{p})=0 $ 得到的。并结合等式5、决策边界为： \[(s_{n}-\frac{O_{n}+\Delta_{n}}{2})^{2}+(s_{p}-\frac{O_{p}+\Delta_{p}}{2})^{2}=C\] 其中， $ C=((O{n}-{n})^{2}+(O{p}-{p})^{2})/4 $ 。
等式7显示了决策边界为圆形，如图1 (b)。所示圆的中心在 $ s{n},=,(O_{n},+,{n})/2,s{p},=,(O_{p},+,{p})/2 $ 处，其半径等于 $ {} $ 。
在等式中有五个超参数，即等式5的 $ O_p $ 、 $ O_n $ 和等式6的 $ $ ， $ {p} $ 和 $ {n} $ 。我们通过设置 $ {O}{p}=1+m,{O}{n}=-m,{p}=1-m $ 和 $ {n}=m $ 来减少超参数。因此，在等式7中的决策边界减少为： \[\left(s_{n}-0\right)^{2}+\left(s_{p}-1\right)^{2}=2m^{2}\] 有了等式8中定义的决策边界，我们对Circle损失有了另一个直观的解释。其目的是优化 $ {s}{m} $ 和 $ {s}{n} $ 。参数 $ m $ 控制着决策边界的半径，可以看作一个松弛因子。换句话说，Circle损失期望 $ s{p}^{i}-m $ 和 $ s_{n}^{j}m $ 。
因此，只有两个超参数，即尺度因子 $ $ 和松弛度 $ m $ 。我们将在第4.5节中实验分析 $ m $ 和 $ $ 的影响。

3.3.Circle损失的优点

Circle损失相对于 $ s_{n}^{j} $ 和 $ s_{p}^{i} $ 的梯度推导如下： \[\frac{\partial\mathcal{L}_{c i r c l e}}{\partial s_{n}^{j}}=Z\frac{\exp\left(\gamma((s_{n}^{j})^{2}-m^{2})\right)}{\sum_{l=1}^{L}\exp\left(\gamma((s_{n}^{l})^{2}-m^{2})\right)}\gamma(s_{n}^{j}+m),\]

和

\[\frac{\partial\mathcal{L}_{c i r c l e}}{\partial s_{p}^{i}}=Z\frac{\exp\left(\gamma((s_{p}^{i}-1)^{2}-m^{2})\right)}{\sum_{k=1}^{K}\exp\left(\gamma((s_{p}^{k}-1)^{2}-m^{2})\right)}\gamma(s_{p}^{i}-1-m),\]

其中 $ Z=1-(-_{c i r c l e}) $ 。
在二值分类的小场景下（或只有一个 $ s_n $ 和 $ s_p $ 时），我们在图2 (c)中可视化了 $ m $ 的不同设置下的梯度，从中我们得出以下三个观察结果：

$ s_n $ 和 $ s_p $ 的平衡优化。我们曾提及过，损失函数最小化 $ (s_{n}-s_{p}) $ 在 $ s_p $ 和 $ s_n $ 上总是具有相等的梯度，这是不灵活的。相比之下，Circle损失展现出动态的惩罚强度。在指定的相似对 $ {s_{n},s_{p}} $ 中，如果 $ s_p $ 比 $ s_n $ 更好（如图2(c)中的 $ A={0.8,0.8} $ ），Circle损失赋予 $ s_n $ 的梯度更大（反之亦然），从而更优先的降低 $ s_n $ 。平衡优化的实验证据详见第4.6节。
逐渐减弱的梯度。在训练开始时，相似性得分偏离最佳值很远，并获得较大的梯度（如图2（c）中的“A”）。随着训练逐渐接近收敛，相似度得分上的梯度相应衰减（如图2(c)中的“B”），进行了温和的优化。第4.5节的实验结果表明，学习效果对 $ $ 的各种设置都是鲁棒性的(在等式6中)，我们将其归因于自动衰减的梯度。
一个（更）明确的收敛目标。Circle损失具有循环决策边界，有利于 $ {} $ 的收敛而不是 $ {}^{} $ 的收敛（图1）。这是因为 $ {} $ 与决策边界上的所有其他点相比， $ s_p $ 和 $ s_n $ 之间的差距最小。换句话说， $ {}^{} $ 在 $ s_p $ 和 $ s_n $ 之间的差距较大，而且本身就更难维持。相比之下，最小化 $ (s_{n}-s_{p}) $ 的损失具有一个齐次的决策边界，即决策边界上的每一个点到达决策边界都具有相同的困难。在实验中，我们观察到，Circle损失导致收敛后的相似度分布更为集中，详见章节4.6和图5。

4.实验

我们综合评估了两种基本学习方法下的有效性：给定类级标签学习和给定成对的标签学习。对于前一种方法，我们在人脸识别（4.2节）和人的再识别（4.3节）任务上评估了我们的方法。对于后一种方法，我们使用细粒度的图像检索数据集（第4.4节），它们相对较小，鼓励使用成对标签进行学习。我们证明了Circle损失在这两种情况下都是有效的。第4.5节分析了这两个超参数的影响，即等式6中的尺度因子 $ $ 和等式8中的松弛因子 $ m $ 。我们证明了在合理的设置下，Circle损失是鲁棒的。最后，第4.6节通过实验证实了Circle损失的特性。