摘要

基于神经网络的聚类方法由于特征提取更有效，通常比传统方法具有更好的性能。大多数现有的深度聚类技术要么先利用图信息从原始数据中提取关键的深度结构，要么简单地利用随机梯度下降（SGD）。然而，他们经常遭受关于降维和聚类的学习步骤的分离。为了解决这些问题，提出了一种具有自适应损失函数和熵正则化特性的深度模糊k-means（DFKM）。DFKM同时进行深度特征提取和模糊聚类，生成更合适的非线性特征映射。此外，DFKM还结合了FKM，从而利用模糊信息来表示深度簇的清晰结构。为了进一步提高模型的鲁棒性，采用自适应权值对目标应用鲁棒损失函数。此外，采用熵正则化的亲和性来提供每个赋值的置信度，相应的隶属度和质心矩阵通过立体解而不是SGD来更新。大量的实验表明，在三个聚类指标下，DFKM比目前最先进的模糊聚类技术具有更好的性能。

索引项-自动编码器（AE）、深度神经网络、图像分割、鲁棒模糊k均值（FKM）、无监督嵌入式聚类。

1.介绍

为了解决这些问题，提出了一种具有自适应损失函数和熵正则化的深度模糊k-均值（DFKM），该模型将模糊聚类合并到AE中，提取更合适的深度特征。利用自适应损失函数[38]来增强对异常值的鲁棒性。图1显示了DFKM的框架。本文的主要贡献总结如下。

聚类嵌入训练神经网络，使声发射能够将数据映射到更合适的深度特征空间。换句话说，DFKM同时进行深度特征提取和聚类。
利用鲁棒损失函数来增强该模型对具有自适应权值的异常值的不敏感性。为了解决这一问题，提出了一种有效的算法，并进一步保证了其收敛到局部最小值。
对亲和矩阵引入熵正则化，为每个分配提供置信度。
在我们的模型中不需要类似的基于图的信息，亲和矩阵和质心矩阵是通过紧密形式的解而不是SGD来更新的。因此，它可以在大数据上有效地执行。

符号：在本文中，所有大写粗体字母表示矩阵，而所有小写粗体字母表示向量。对于矩阵M，$m^i$表示第i个行向量，$m_i$表示第i个列向量，$m_{ij}$是它的$(i,j)$个元素。此外，MT是矩阵M的转置，${\textbf{1}}=[1,1,\cdot\cdot\cdot,1]^{T}$，0表示零矩阵。M > 0表示每个元素都为正。$\|\mathbf{m}\|_{1}$和$\|\mathbf{m}\|_{2}$分别表示$\ell_{1}$范数和$\ell_{2}$范数。$\nabla_{\mathbf{x}}f(\mathbf{x})=[{\frac{\partial f}{\partial x_{1}}},{\frac{\partial f}{\partial x_{3}}},\cdot\cdot,{\frac{\partial f}{\partial x_{n}}}]^{T}$，其中f (x)是一个标量输出函数，而$\nabla_{\mathbf{x}}g(\mathbf{x})=[{\frac{\partial g_{1}}{\partial x}},{\frac{\partial g_{2}}{\partial x}},\cdot\cdot,{\frac{\partial g_{n}}{\partial x}}]^{T}$，其中g (x)是一个向量输出函数。

2.相关工作

A.模糊聚类

B.深度聚类

3.方法

由于传统的核k-means（KKM）和基于谱的聚类方法对大数据难以处理，而KM和非负矩阵分解等有效技术过于简单，应用于非线性数据，因此提出了处理大数据集和非线性分布数据的DFKM。在本节中，我们首先介绍了自适应损失函数和熵正则化的FKM。然后，详细介绍了DFKM的研究细节。

A. 自适应损耗函数

$\ell_{2，1}$范数： \[\|\mathbf{M}\|_{2,1}=\sum_{i}\|\mathbf{n^{i}}\|_{2}\] Frobenius范数： \[\|\mathbf{M}\|_{F}^{2}=\sum_{i}\|\mathbf{m}^{i}\|_{2}^{2}\] 为了利用它们的优点，将一个鲁棒损失函数即自适应损失函数定义为[38]，[40]如下： \[||{\bf M}||_{\sigma}=\sum_{i}{\frac{(1+\sigma)||{\bf m}^{i}||_{2}^{2}}{||{\bf m}^{i}||_{2}+\sigma}}\] 其中，σ是一个权衡参数，它控制对各种类型异常值的鲁棒性。不同σ下向量的自适应损失函数说明如图2所示。

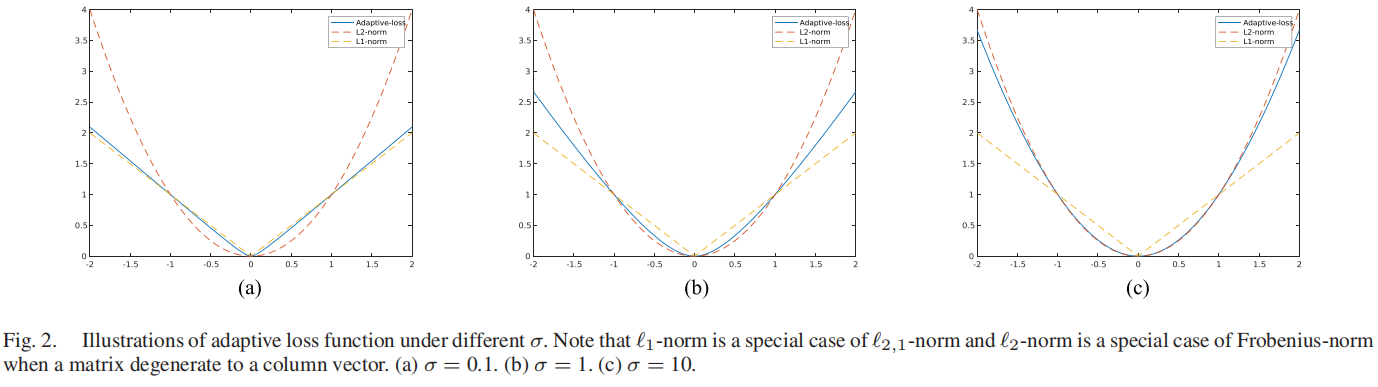
从图2中可知，自适应损失函数在2,1-范数和平方弗罗比尼乌斯范数之间进行插值，它继承了平方弗罗比尼乌斯范数的平滑性。$\|\mathbf{M}\|_{\sigma}$的性质总结如下。

$\|\mathbf{M}\|_{\sigma}$是二倍微分、凸和非负的，因此它适合作为一个损失函数。
如果$\forall i$，$\|\mathbf{m}_{i}||\ll\sigma$，则$||\mathbf{M}||_{\sigma}\rightarrow\ {\begin{array}{l}{\frac{1+\sigma}{\sigma}}\end{array}}||\mathbf{M}||^{2}_{F}$。
如果$\forall i$，$\|\mathbf{m}_{i}||\gg\sigma$，则$||\mathbf{M}||_{\sigma}\rightarrow\ {\begin{array}{l}{(1+\sigma)}\end{array}}||\mathbf{M}||_{2,1}$。
如果$\sigma\to0$，则$||\mathbf{M}||_{\sigma}\rightarrow\ {\begin{array}{l}\end{array}}||\mathbf{M}||_{2,1}$。
如果$\sigma\to\infty$，则$||\mathbf{M}||_{\sigma}\rightarrow\ {\begin{array}{l}\end{array}}||\mathbf{M}||^{2}_{F}$。

B. 具有加权自适应损失函数的FKM

对于数据数为N的任意数据矩阵$\mathbf{X}=\left[\mathbf{x}_{1},\mathbf{x}_{2},\ldots,\mathbf{x}_{N}\right]$，将具有熵正则化的FKM的目标函数定义为[26]，[39] \[\operatorname*{min}_{c_j, u_{ij}}\sum_{i=1}^{N}\sum_{j=1}^{k}u_{i j}\vert\vert{\bf x}_{i}-{\bf c}_{j}\vert\vert_{2}^{2}+\gamma u_{i j}\ \mathrm{log}\,u_{i j}\\\mathrm{s.t.}\,\,\sum_{j=1}^{k}u_{i j}=1,0\lt u_{i j}\lt 1\] 其中，$\gamma$是控制$u_{ij}$分布的权衡参数。当$\gamma\rightarrow\infty,\,u_{i j}\rightarrow\,{\textstyle\frac{1}{N}}$时。
提出了一种新的具有自适应损失函数的FKM代价函数，如下[41]： \[\sum_{i=1}^{N}\sum_{j=1}^{k}u_{i j}{\frac{(1+\sigma)||{\bf x}_{i}-{\bf c}_{j}||_{2}^{2}}{||{\bf x}_{i}-{\bf c}_{j}||_{2}+\sigma}}+\gamma u_{i j}\ \mathrm{log}\,u_{i j}\]

可以重写为

\[\operatorname*{min}_{c_j, u_{ij}}\sum_{i=1}^{N}\sum_{j=1}^{k}u_{i j}\|{\bf x}_{i}-{\bf c}_{j}\|_{\hat{\sigma}}+\gamma u_{i j}\ \mathrm{log}\,u_{i j}\\\mathrm{s.t.}\,\,\sum_{j=1}^{k}u_{i j}=1,0\lt u_{i j}\lt 1\]

其中，$\|\mathbf{M}\|_{\hat\sigma}$相当于任何向量$\mathbf{m}\in\mathbb{R}^{d}$的$\|\mathbf{M^T}\|_{\sigma}$。
在下一节中，我们开发了一个有效的算法来解决上面问题。

C. DFKM的代价函数

$$ \[\begin{array}{ll}J_1=||{\bf H}^{(M)}-\mathrm{X}||_{F}^{2}\\J_2=\sum_{i=1}^{N}\sum_{j=1}^{k}u_{i j}||\mathbf{h}_{i}^{({\frac{M}{2}})}-\mathbf{c}_{j}||_{\hat{\sigma}}+\gamma u_{i j}\log u_{i j}\\J_3=\sum_{m=1}^{M}||\mathbf{W}^{(m)}||_{F}^{2}+||\mathbf{b}^{(m)}||_{2}^{2} \end{array}\]

{c}$$

因此，通过将熵正则化和自适应损失嵌入，提出了DFKM模型 \[\begin{aligned}& \underset{\operatorname{W}^{(m)}, \operatorname{D}^{(m)}, \mathbf{C}}{\text{minimize}}& & J_1 + \lambda_{1}J_2 + \lambda_{2}J_3 \\& \text{subject to}& & \sum_{j=1}^{k}u_{i j}=1, \quad 0 < u_{i j} < 1, \quad \forall i\end{aligned}\] 其中，λ1和λ2是权衡参数。$\mathbf{c}_{j}\in\mathbb{R}^{d^{\prime}}$是低维特征空间中的第j个簇质心，具有$d^{\prime}=d^{(\frac{M}{2})}$。

J1、J2和J3被设计为不同的目的。J1保证了重构误差的最小值。j2是问题（10）中提出的具有自适应损失函数的FKM的代价函数。因此，λ1是重建和FKM之间的权衡参数。请注意，如果我们将λ1设置为一个较大的值，即较小的J2，那么由于重建不良，该模型的性能将不会太理想。J3是一种正则化方法，用于避免与正则化参数λ2过拟合的不良事件。术语J3也能够防止声发射生成一个平凡的映射。

因此，DFKM是将原始数据投影到一个非线性的低维特征空间上，并通过非线性映射特征同时学习一个软聚类隶属度矩阵。

4.优化算法

在本节中，我们首先开发了一个有效的算法来求解自适应（10）中损失函数的FKM，该算法保证收敛到局部最小值。然后，提出了一种求解（14）中DFKM损失函数的算法。

A. 加权自适应损失函数的优化

B. DFKM的优化

5.实验

6.结论

在本文中，我们提出了一种基于神经网络的聚类方法DFKM，该方法采用了熵正则化和具有自适应权值的鲁棒损失函数。通过结合AE和鲁棒FKM，DFKM将原始数据映射到一个更合适的空间，从而获得更好的性能。换句话说，DFKM同时执行聚类和特征提取，而不是将它们分成两个单独的步骤。此外，隶属度矩阵和质心矩阵通过近似解而不是SGD进行更新，使相应的优化算法快速收敛。大量的实验表明，在三个聚类指标下，我们的模型比目前最先进的模糊聚类算法获得了更好的性能。此外，DFKM还获得了更好的图像分割结果，验证了该模型的优越性。