EAGLE:Eigen Aggregation Learning for Object-Centric Unsupervised Semantic Segmentation
摘要
语义分割天生依赖于大量的像素级注释数据,导致了无监督方法的出现。其中,利用自监督视觉转换器进行无监督语义分割(USS)在表达深度特征方面取得了稳步的进展。然而,对于使用复杂对象对图像进行语义分割,一个主要的挑战仍然存在:在补丁级特征中缺乏显式的对象级语义编码。这种技术限制往往导致对具有不同结构的复杂对象的分割不足。为了解决这一差距,我们提出了一种新的方法,EAGLE,它强调无监督语义分割的对象中心表示学习。具体地说,我们介绍了EiCue,这是一种光谱技术,通过来自深度图像特征的语义相似度矩阵和来自图像的颜色亲和度的特征基来提供语义和结构线索。此外,通过将我们的以对象为中心的对比损失与EiCue结合起来,我们指导我们的模型学习具有图像内和图像间对象-特征一致性的对象级表示,从而提高语义的准确性。在COCO-Stuff、城市景观和波茨坦-3数据集上的广泛实验证明了鹰的最新结果,在复杂场景中具有准确和一致的语义分割。
1.引言
特别是,最近的基于网络的方法经常利用一个自监督的视觉变压器(ViT)来学习补丁级的特征。虽然它们的补丁级特性被证明对进一步的USS推理步骤(例如,K-means)很有用,但底层的对象级语义并没有明确地强加在这些补丁级特性中。要掌握“对象级语义”,请考虑一个覆盖层对象的示例,如图1b的第二行所示。与任何对象一样,毯子很容易出现在不同的图像中使用不同的颜色和纹理。如果没有适当的对象级语义,对应于不同覆盖区域的特征可能会导致截然不同的特征表示。但理想情况下,对应于各种毯子的特性应该映射到相似的特性,即对象级语义。因此,如果没有仔细强加对象级语义,具有不同结构和形状的复杂对象可以很容易地划分为带有错误类标签的多个段,或者与附近不同类标签的段合并。因此,在USS中,必须付出巨大的努力来学习具有强对象级语义的本地特性(例如,补丁级)。
我们为USS提供的以对象为中心的表示学习旨在捕获这种对象级的语义。具体来说,我们首先需要一个在以对象为中心的视图中的语义或结构线索。以往的一些研究利用K-means或超像素等聚类方法来获得语义线索[20],但它们主要关注一般的图像模式,而不是对象的语义或结构表示。在这里,我们提出了EiCue,它通过特征基提供对象的语义和结构线索。具体地说,我们利用从ViT
[6,14]得到的投影深度图像特征得到的语义相似度矩阵和图像的颜色亲和矩阵来构造图拉普拉斯算子。相应的特征基捕获了对象[32,61]的底层语义结构,为后续的对象级特征细化步骤提供了软指导。回想一下,对象的精确对象级语义必须在不同图像之间保持一致。我们的以对象为中心的对比学习框架明确地将这些特征强加为一个新的对象级的对比损失。具体来说,基于EiCue中的对象线索,我们为每个对象推导出可学习的原型,从而使图像内部和图像间的对象-特征保持一致性。通过这个全面的学习过程,我们的模型有效地捕获了图像中的固有结构,允许它精确地识别语义上可信的对象表示,这是推进现代基于特征的USS的关键。
贡献。我们的主要贡献如下:
- 我们提出EiCue,使用一个可学习的图拉普拉斯行列式,以获得对图像中的潜在语义和结构细节的更深刻的理解。
- 我们设计了一个以对象为中心的对比学习框架,它利用EiCue的光谱基础来构建鲁棒的对象级特征表示。
- 通过一系列全面的实验支持,无监督语义分割证明了我们的鹰在无监督语义分割上取得了最先进的性能。
3.方法
当我们开始描述图2中所示的完整管道时,让我们首先介绍基于预训练模型的核心USS框架,如之前的工作[16,49]。
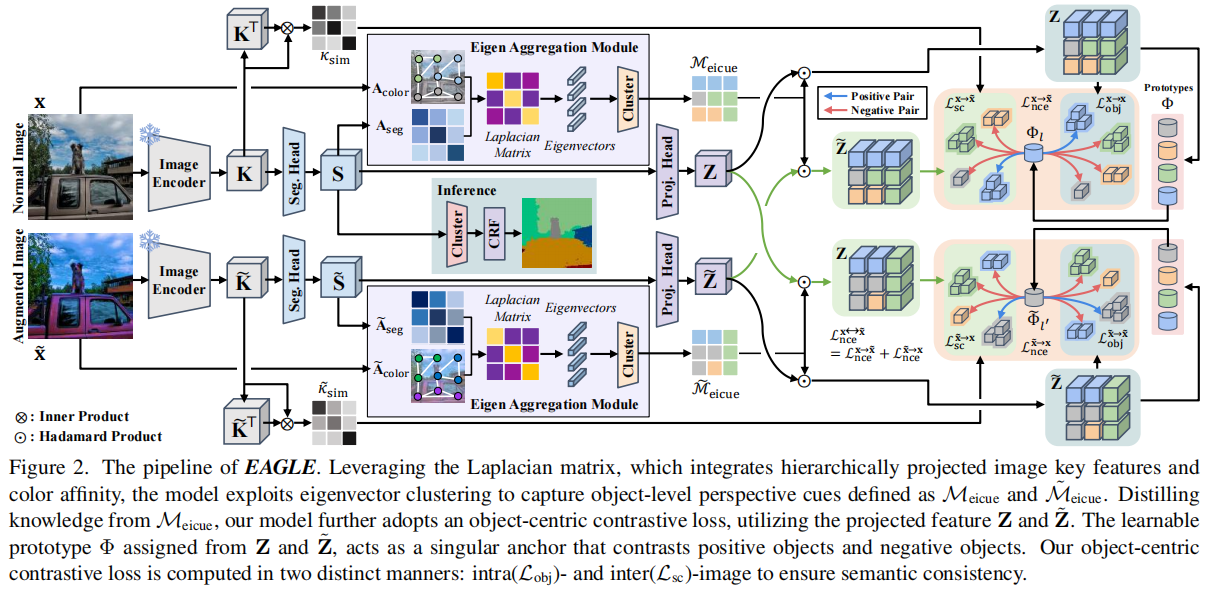
图2。EAGLE的管道。利用拉普拉斯矩阵,它集成了分层投影的图像关键特征和颜色亲和性,该模型利用特征向量聚类来捕获定义为Meicue和M˜˜的对象级透视线索。利用Meicue的提炼知识,我们的模型进一步采用了一个以对象为中心的对比损失,利用投影特征Z和Z˜。由Z和Z˜分配的可学习的原型Φ,作为一个单一的锚,对比正对象和负对象。我们的以对象为中心的对比损失以两种不同的方式计算:内部(Lobj)和内部(Lsc)图像,以确保语义一致性。
3.1.预处理
未标记的图像。我们的方法完全建立在一组图像上,没有任何注释,表示为\(\mathbf{X}=\left\{\mathbf{x}_b\right\}_{b=1}^B\),其中B是一个小批处理中的训练图像的数量。我们还利用光度增强策略P来获得一个增强图像集\(\tilde{\mathbf{X}}=\left\{\tilde{\mathbf{x}}_b\right\}_{b=1}^B=P(\mathbf{X})\)。
预训练特征k。然后,对于每个输入图像\(\mathbf
x_b\),我们使用自我监督预训练视觉transformer[6]作为图像编码器\(\mathcal{F}\)获得分层注意关键特征从最后三个块\(\mathbf{K}_{L-2}=\mathcal{F}_{L-2}\left(\mathbf{x}_b\right)\),\(\mathbf{K}_{L-1}=\mathcal{F}_{L-1}\left(\mathbf{x}_b\right)\),\(\mathbf{K}_{L}=\mathcal{F}_{L}\left(\mathbf{x}_b\right)\),其中L−2,L−1,L是第三层,第二到最后层,和最后一层,分别。然后,我们将它们连接到一个单一的注意张量\(\mathbf{K}=\left[\mathbf{K}_{L-2} ;
\mathbf{K}_{L-1} ; \mathbf{K}_L\right] \in \mathbb{R}^{H \times W \times
D_K}\)。同样,我们对增广图像 \(\mathbf{\tilde{x}}\)
应用相同的程序,得到了它的注意张量\(\tilde{\mathbf{K}} \in \mathbb{R}^{H \times W
\times
D_K}\)。
语义特征S。虽然K包含了一些基于注意机制的对象的结构信息,但由于没有足够的语义信息来进行直接推理。因此,为了进一步细化特征,我们计算了语义特征\(\mathbf{S}=\mathcal{S}_\theta(\mathbf{K}) \in
\mathbb{R}^{H \times W \times D_S}\)和\(\tilde{\mathbf{S}}=\mathcal{S}_\theta(\tilde{\mathbf{K}})
\in \mathbb{R}^{H \times W \times D_S}\),其中\(S_\theta: \mathbb{R}^{H \times W \times D_K}
\rightarrow \mathbb{R}^{H \times W \times
D_S}\)是一个可学习的非线性分割头。为简洁起见,补丁的总数,记为H×W,将被称为N。
推理。在推理时间内,给定一幅新图像,其语义特征S成为进一步聚类的基础,采用传统的评估设置,如K-means聚类和线性探测。因此,与之前预先训练的基于特征的USS工作[16,49]一样,训练\(\mathcal{S}_\theta\)以无监督的方式输出强语义特征S是当代USS框架的基本框架。接下来,我们将在图2中描述管道的其余部分,这与我们对生成强大的对象级语义特征的方法贡献相对应。
3.2.通过特征聚合模块进行的EiCue
直觉告诉我们,“语义上可信”的对象级片段是精确捕获对象结构的像素组,即使在复杂的结构方差下也是如此。例如,一个汽车部件必须包含其所有部件,包括挡风玻璃、车门、车轮等。它们都可能以不同的形状和视图出现。然而,如果没有提供对象级语义的像素级注释,这将成为推断具有零对象级结构优先级的底层结构的一个极具挑战性的任务。
从这一实现中,我们的模型EAGLE首先基于特征相似度矩阵的特征基,得到一个强大而简单的语义结构线索,即EiCue,如图3所示。
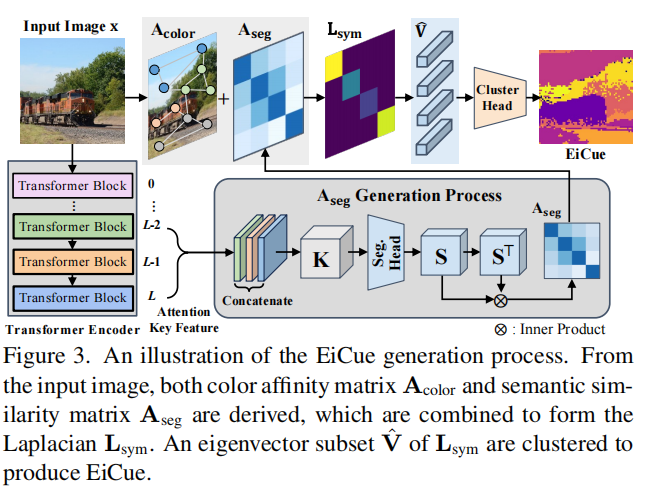
图3.EiCue生成过程的说明。从输入的图像中,推导出颜色相似度矩阵\(\mathbf{A}_{color}\)和语义相似度矩阵\(\mathbf{A}_{seg}\),并将其组合成拉普拉斯算子\(\mathbf{L}_{sym}\)。将Lsym的一个特征向量子集\(\mathbf{\hat{V}}\)聚类产生EiCue。
具体来说,我们使用著名的光谱聚类[7,39,51]来获得无监督的特征表示,以捕获底层的非线性结构,以处理具有复杂模式的数据。这通常只在颜色空间中工作,但可以很容易地扩展到利用由任何特征构造的相似性矩阵。我们观察到,这种光谱方法对于复杂的真实世界的图像特别有用,如图4所示。

图4.可视化在特征聚合模块中由S得到的特征向量。这些特征向量不仅区分不同的对象,还识别语义相关的区域,突出了EiCue如何有效地捕获对象的语义和边界。
EiCue结构。让我们详细描述构建EiCue的过程,如图3所示。总体框架一般遵循一般的谱聚类:从 (1)邻接矩阵\(\mathbf{A}\)中构造(2)拉普拉斯算子\(\mathbf{L}\),(3)对\(\mathbf{L}\)进行特征分解,得到特征基\(\mathbf{V}\),利用特征特征进行聚类。我们将在下面描述每个步骤。
3.2.1邻接矩阵的构造
我们的邻接矩阵由两个组成部分组成:(1)颜色相似度矩阵和(2)语义相似度矩阵。
(一)颜色相似度矩阵\(\mathbf{A}_{color}\):
(二)语义相似度矩阵\(\mathbf{A}_{seg}\):
(三)邻接矩阵\(\mathbf{A}\):
3.2.2特征分解
为了构造基于\(\mathbf{A}\)的EiCue,我们创建了一个拉普拉斯矩阵。形式上,拉普拉斯矩阵表示为\(\mathbf{L} = \mathbf{D}−\mathbf{A}\),其中\(\mathbf{D}\)是\(\mathbf{A}\)的度量矩阵,定义为\(\mathbf{D}(i, i)=\sum_{j=1}^N \mathbf{A}(i, j)\)。在我们的方法中,我们利用归一化的拉普拉斯矩阵来增强其聚类能力。将对称归一化拉普拉斯矩阵\(\mathbf{L}_{sym}\)定义为\(\mathbf{L}_{\text {sym }}=\mathbf{D}^{-\frac{1}{2}} \mathbf{L} \mathbf{D}^{-\frac{1}{2}}\)。然后,通过对\(\mathbf{L}_{sym}\)的特征分解,计算得到特征基\(\mathbf{V} \in \mathbb{R}^{N \times N}\),其中每一列对应于一个唯一的特征向量。然后,我们提取与k个最小特征值对应的k个特征向量,并将它们连接到\(\mathbf{\hat{V}} \in \mathbb{R}^{N \times N}\)中,其中第i行对应于第i个补丁的k个维特征。
3.2.3可微特征聚类
在得到特征向量\(\mathbf{\hat{V}}\)后,我们进行特征向量聚类过程,提取的EiCue表示为\(\mathcal{M}_{\text {eicue }} \in \mathbb{R}^N\)。为了聚类特征向量,我们利用了一个基于\(\hat V\)和\(C\)之间的余弦距离[36]的小批次K-means算法,记为\(P=\hat VC\)。集群中心\(\mathbf{C} \in \mathbb{R}^{k \times C}\)由可学习的参数组成。为了学习C,我们进一步训练了损失定义如下: \[\mathcal{L}_{\text {eig }}^{\mathrm{x}}=-\frac{1}{N} \sum_{i=1}^N\left(\sum_{c=1}^C \Psi_{i c} \mathbf{P}_{i c}\right),\] 其中C表示预定义的类数,\(\Psi:=\operatorname{softmax}(\mathbf{P})\),\(\mathbf P_{ic}\)和\(\Psi_{ic}\)表示第i个补丁和第C个簇数。我们将同样的过程应用于增广图像\(\tilde{\mathrm{x}}\),得到\(\mathcal{L}_{\text {eig }}^{\tilde{\mathrm{x}}}\)。通过最小化\(\mathcal{L}_{\text {eig }}=\frac{1}{2}\left(\mathcal{L}_{\text {eig }}^{\mathrm{x}}+\mathcal{L}_{\text {eig }}^{\tilde{\mathrm{x}}}\right)\),我们可以获得能够实现更有效的聚类的聚类中心。然后我们得到EiCue为 \[\mathcal{M}_{\text {eicue }}(i)=\underset{c}{\operatorname{argmax}}\left(\mathbf{P}_{i c}-\log \left(\sum_{c^{\prime}=1}^C \exp \left(\mathbf{P}_{i c^{\prime}}\right)\right)\right) .\] 随着聚类质心精度的提高,EiCue促进了基于语义结构的patch i到对应对象的映射。这是一个有意义的线索,可以强调不同对象之间的语义区别,从而增强特征嵌入的辨别能力。
备注。虽然与之前使用特征分解的工作[38]相似,但我们的方法的不同之处在于使用可训练的分割头增强特征向量S,而不是它们依赖于静态向量(即K)。我们的方法通过可微特征聚类增强了S的可学习性和适应性,允许图的拉普拉斯语义和对象语义进化。这种EiCue与学习过程的动态集成清楚地将我们的方法与之前的应用区分开来。

3.3.基于EiCue的ObjNCE损失
对于一个成功的语义分割任务,不仅要准确地对每个像素的类进行分类,还要聚合对象表示并创建一个反映对象语义表示的分割图。从这个角度来看,在以对象为中心的视角下学习关系在语义分割任务中尤为重要。为了捕捉对象之间的复杂关系,我们的方法结合了一个以对象为中心的对比学习策略,名为ObjNCELoss,由EiCue指导。该策略旨在细化特征嵌入S的鉴别能力,强调不同对象语义之间的区别。在继续之前,我们映射投影特征$ ^{N D_{Z}} \(和\){} , , ^{N D_{Z}} \(,分别使用线性投影头\){}{}\(,来自重塑的\) ^{N D{Z}} \(和\){} , , ^{N D_{S}} \(。虽然\)D_S\(和\)D_Z$的实际尺寸大小保持不变,但为了便于解释,我们使用了不同的符号。
3.3.1对象样机
3.3.2以对象为中心的对比损失
3.4.总目标
(未完不待续)
为了构造基于\(\mathbf{A}\)的EiCue(假设是为了增强聚类效果的操作),我们使用了图的拉普拉斯矩阵,它能够很好地反映数据中的几何结构和局部关联性。以下是详细解释过程:
1.
构造邻接矩阵\(\mathbf{A}\)
\(\mathbf{A} \in \mathbb{R}^{N \times
N}\)是从特征变量中提取出来的,表征数据中各个样本(通常是图像中的补丁或像素)之间的相似性。这个相似性可以通过各种方式计算,比如基于特征的欧氏距离或高斯相似性函数。特征变量的大小为\(B \times C \times N\),其中:
- \(B\)是批量大小,
- \(C\)是特征的通道数(即每个特征向量的维度),
- \(N = H \times W\)是空间维度的展平结果,通常表示图像补丁或像素的数量。
在这里,\(N = 256 \times 256 = 65536\),表示图像的像素总数。
2.
构造度量矩阵\(\mathbf{D}\)
度量矩阵\(\mathbf{D}\)是对角矩阵,表示邻接矩阵\(\mathbf{A}\)中每个节点的度。它通过计算每个节点连接到其他节点的总权重来定义:
\[\mathbf{D}(i,i) = \sum_{j=1}^N \mathbf{A}(i,j)\] 这意味着度矩阵的每个对角元素表示与节点\(i\)相连的边的总权重。
3.
构造拉普拉斯矩阵\(\mathbf{L}\)
拉普拉斯矩阵\(\mathbf{L}\)表示为:
\[\mathbf{L} = \mathbf{D} - \mathbf{A}\] 这是标准的无归一化拉普拉斯矩阵,它反映了每个节点和其相邻节点之间的差异。拉普拉斯矩阵的特性使得它在图形信号处理中广泛用于捕捉图结构。
4.
归一化拉普拉斯矩阵\(\mathbf{L}_{sym}\)
为了增强聚类效果,我们使用对称归一化的拉普拉斯矩阵\(\mathbf{L}_{sym}\),其形式为:
\[\mathbf{L}_{\text{sym}} = \mathbf{D}^{-\frac{1}{2}} \mathbf{L} \mathbf{D}^{-\frac{1}{2}} = \mathbf{I} - \mathbf{D}^{-\frac{1}{2}} \mathbf{A} \mathbf{D}^{-\frac{1}{2}}\] 对称归一化拉普拉斯矩阵能够更好地处理图的不同节点度分布的问题,使得高度节点和低度节点在拉普拉斯矩阵中得到更加平衡的对待。
5.
特征分解
对\(\mathbf{L}_{\text{sym}}\)进行特征值分解,得到:
\[\mathbf{L}_{\text{sym}} = \mathbf{V} \mathbf{\Lambda} \mathbf{V}^{\top}\] 其中,\(\mathbf{V} \in \mathbb{R}^{N \times N}\)是特征向量矩阵,\(\mathbf{\Lambda}\)是对角的特征值矩阵。每一列\(\mathbf{V}_i\)对应于一个特征向量,且与\(\mathbf{\Lambda}\)中的特征值相对应。
6.
提取特征基
我们提取与\(k\)个最小特征值对应的\(k\)个特征向量,并将它们连接成矩阵\(\mathbf{\hat{V}} \in \mathbb{R}^{N \times
k}\)。这意味着:
- 选取\(k\)个最小的特征值,这些特征值的特征向量能够表示数据的局部流形结构。
- 特征向量\(\mathbf{V}\)的第\(i\)行对应于图中第\(i\)个节点的特征表示(通常是图像中的某个像素或补丁)。
- \(\mathbf{\hat{V}}\)包含每个节点在选定的\(k\)维特征空间中的表示,这将用于后续的聚类任务。
