Fuzzy_Machine_Learning
Fuzzy Machine Learning: A Comprehensive Framework and Systematic Review
摘要
机器学习的力量来自各种学科,包括计算机科学、认知科学和统计学。虽然机器学习在理论和实践上都取得了很大的进步,但其方法在处理复杂情况和高度不确定的环境时存在一定的局限性。数据的不足、不精确的观察和模糊的信息/关系都会混淆传统的机器学习系统。为了解决这些问题,研究人员从不同的方面整合了机器学习和模糊技术,包括模糊集、模糊系统、模糊逻辑、模糊测度、模糊关系等。本文从模糊机器学习,从理论到应用方法,总体目标是概述模糊机器学习领域的最新进展。为此,将所讨论的概念和框架分为五类:1)模糊经典机器学习;2)模糊迁移学习;3)模糊数据流学习;4)模糊强化学习;和5)模糊推荐系统。所提供的文献将使研究人员深入了解模糊机器学习研究的进展及其应用。
I.介绍
在动态的技术领域,机器学习已经深刻地改变了各个领域。它通过解码复杂的数据模式,推动人工智能的进步,并影响我们如何参与信息和理解计算系统的能力,以此来引领创新。然而,在大多数现有的机器学习方法中,具有不确定性的场景的准确性会受到影响,例如唯一可用的观测是不精确的或数据是有噪声或不完整的。此外,许多真实世界的数据集包含不确定的关系,传统的机器学习方法通常发现很难识别或处理这些结构。为了解决这些问题,研究人员已经使用模糊技术集成到机器学习中,称为模糊机器学习(FML)[1]作为一种解决方案,因为模糊技术能够成功地处理不确定性。FML系统融合机器学习算法与模糊技术,如模糊集[2],模糊系统[3],模糊聚类[4],模糊关系[5],模糊措施[6],模糊匹配[7],模糊优化[8]等等,建立新的模型更健壮的许多和各种类型的不确定性在现实世界的问题。
FML在复杂和动态(不确定)的环境中是一个宝贵的盟友,展示了提高其功效的实质性优势。与传统的机器学习方法不同,通常基于模糊集[9]和模糊理论[10]的模糊技术擅长捕捉和导航动态场景中固有的细微不确定性。它们建模不确定性的内在能力使其能够优雅地适应动态环境中不断变化的模式。在传统模型可能会动摇或难以跟上步伐的情况下,模糊技术作为鲁棒的问题解决者出现,提供了真实数据[11]中固有模糊性的更准确的表示。
- 模糊集[2]可以用来表示模糊或模糊的概念和数据,例如在语言变量、噪声或不完整数据和区间值数据中常见的数据。模糊集增强了算法在不确定和复杂情况下做出决策的能力,这在现实世界条件可能不可预测的应用中特别有用,如机器人或自动驾驶汽车。
2. 基于模糊规则的系统[3]可以提供一个透明和可解释的预测框架。基于模糊规则的系统使用语言规则来表示知识,因此,可以用来对系统所做出的决策进行解释。这在医疗诊断等应用程序中很有用。
3. 模糊聚类[4]是一种著名的聚类方法,它可以通过识别传统聚类方法不易识别的数据模式来改进机器学习算法。模糊集群不仅允许重叠的集群,而且还可以确定地处理可能不属于任何特定集群的数据点。这在图像识别等应用程序中很有用。
4. 模糊关系[5]可以提供变量或数据点之间关系的更灵活和微妙的表示。它们还可以捕获非线性关系,以使更准确和更有表现力的机器学习模型成为可能。此外,模糊关系在处理多模态数据或从多个来源组装的数据时是有用的,因为研究人员可以定义不同模态之间的模糊关系,从而得到一个更全面和准确的模型。
在过去的十年里,在高质量的期刊和会议论文集上,已经有超过50万篇包含“模糊”和“机器学习”字样的文章。然而,这些文章都没有提供关于最近关于FML的文献的全面综述。以前在该地区进行的几次调查只对FML的某些子领域提供了有价值的见解。例如,Baraldi和Blonda
[12]提供了模糊聚类的模式识别算法,而Skrjanc等人。[13]总结了基于进化模糊规则和神经模糊网络(NFNs)的模型,用于聚类、回归、识别和分类问题。此外,Zheng等人[14]回顾了最近在将深度学习模型与模糊系统融合方面的工作。此外,近十年来,在FML中出现了新的子领域,如模糊迁移学习和模糊数据流学习。提供一份调查报告来概述这些新的子领域是很重要的。由于这些原因,有必要进行一个新的、更全面的、更最新的FML调查。本文主要针对利用模糊技术提高机器学习方法性能的研究人员,特别是在涉及复杂或不确定因素的情况下。
本研究中纳入的研究分为以下三个步骤。
步骤1)确定并确定要搜索的适当的发布数据库集。我们搜索了科学直接数据库、ACM数字图书馆数据库、IEEE
Xplore数据库和SpringerLink数据库等著名的数据库。这些研究提供了关于机器学习和FML的研究论文的全面参考书目。
步骤2)文章的初步筛选:第一次搜索是基于关键词。这些文章:
a)提出了FML领域的新理论、算法或方法;或b)报告了一个围绕FML算法构建的应用程序。
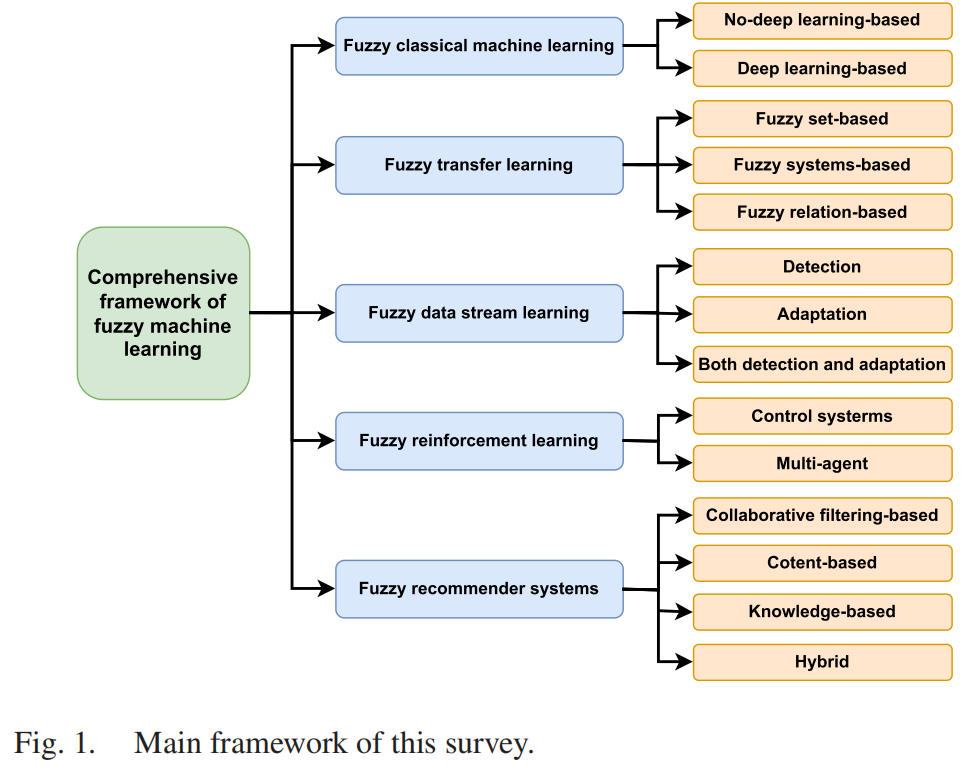
步骤3)对陈述结果进行过滤:将步骤2选择的文章分为五组,分为分为部分:a)模糊经典机器学习;b)模糊迁移学习;c)模糊数据流学习;d)模糊强化学习(RL);e)模糊推荐系统。此时,我们对文章进行了最后的筛选(见图1)。如果一项研究证明足够,则保留:
a)新颖性,即在过去十年内发表;b)影响,即它发表在高质量的期刊/会议上或高被引用。
本文的主要贡献如下。
- 全面总结了FML领域的发展和成果。这一领域的工作主要分为五大类进行讨论。
2. 本文分析了现实场景中传统机器学习方法的缺点,然后解释了FML如何被用于解决这些问题。所提供的见解旨在帮助研究人员了解FML研究及其应用的发展背景。
3. 它提供了一个对最先进的(SOTA)FML模型的批判性的讨论,并概述了未来研究的方向。
II.FML的基本概念
在本节中,我们将简要介绍一些相关的数学概念,来说明如何将模糊逻辑集成到迁移学习、数据流学习、RL和推荐系统中。这些概念应该可以帮助研究人员更好地理解以下章节中介绍的文章。
A.模糊迁移学习
迁移学习[15]试图通过利用来自另一个领域(源)的知识来训练在一个领域(目标)中表现良好的模型,该领域与前一个领域具有不同的分布或学习任务。本节介绍了两个具有代表性的模糊迁移学习框架: 1)基于模糊规则的[16]和2)基于模糊等价的[17]。
1)基于模糊规则的迁移学习框架[16]:
设\(\mathcal{S}=\{S^{1},S^{2},\cdot\cdot\cdot,\mathcal{S}^{N}\}\)表示一组源域,其中\({\cal S}^{n}=\{({\bf
x}_{i}^{\mathrm{S}_{n}},{y}_{i}^{\mathrm{S}_{n}})|{\bf
x}_{i}^{\mathrm{S}_{n}}\in\chi^{n},{y}_{i}^{\mathrm{s}_{n}}\in\mathcal{Y}\}_{i=1}^{m_{n}}\),\(n\in [N]\)和\(({\bf
x}_{i}^{\mathrm{S}_{n}},{y}_{i}^{\mathrm{S}_{n}})\)是n源域的第一对输入输出数据对。这里,\(\chi^{n}\subset\mathbb{R}^{p}\)表示每个源域的特征空间,\(\mathcal{Y}\)是一个响应空间(\(\mathcal{Y} =
\{1,2,...,K\}\)给定一个分类任务,\(\mathcal{Y}\subset\mathbb{R}\)给定一个回归任务)。\(\mathcal{T}=\{\bf x_{i}^{T}|{\bf
x}_{i}^{T}\in\chi^{T}\}_{i=1}^{m_{t}}\)是未标记的目标域(对于无监督的场景),其中\(\chi^{T}\subset\mathbb{R}^{p}\)是目标域的特征空间。在同质情况下,\(X^1\),...,\(X^N\)和\(X^T\)具有相同数量的特征,而在异构情况下,它们包含不同数量的特征。
我们将\(\mathcal{R}=\{\mathcal{R}^{1},\mathcal{R}^{2},\dots,\mathcal{R}^{N}\}\)表示为S构造的模糊规则空间,其中\(\mathcal{R}=\{r(v_{l}^{S_{n}},a_{l}^{S_{n}})\}_{l=1}^{l_{n}},n\in[N]\)是\(\mathcal{S}^n\)的第n个规则集。这里,规则\(r(v_{l}^{S_{n}},a_{l}^{S_{n}})\)表示为
\[\begin{array}{l}{\mathrm{if~x}_{i}^{S_{n}\mathrm{~is~}A_{l}({\bf
x}_{i}^{S_{n}},v_{l}^{S_{n}}),}}\\
{\mathrm{then~}y_{i}^{S_{n}\mathrm{~is~}P_{l}({\bf
x}_{i}^{S_{n}},a_{l}^{S_{n}}),}}\\ {l=1,2,\ldots..\cdot
l_{n}.}\end{array}\] 其中\(\mathcal{R}^T\)表示得到的目标域\(\mathcal{T}\)的模糊规则。
最后,将\(\Phi=\{\Phi^{1},\Phi^{2},\dots,\Phi^{N}\}\)表示为\(\mathcal{R}\)(例如,线性组合)的结果,其中\(\Phi^{n}(\mathcal{R}^{n},\mu_{n}),n\in[N]\)是\(\mathcal{R}^n\)的第n个结果。因此,基于模糊规则的迁移学习的目的是利用\(\mathbf{D}=\{\mathcal{S},\mathcal{R},\Phi\}\)的知识拟合目标域的数据,即得到\(\mathcal{R}^T\)和\(\mathcal{R}^T\)的结果。
2)基于模糊等价的迁移学习框架[17]:
与基于模糊规则的迁移学习不同,该框架应用源域和目标域特征之间的模糊等价关系来代替模糊规则。设\(\mathcal{U}=\{\mathcal{U}^{1},\mathcal{U}^{2},\dots,\mathcal{U}^{N}\}\)表示\(\mathcal{S}\)中特征的隶属函数空间,其中\(\mathcal{U}^{n}=\{\mu_{1}^{S_{n}},\mu_{2}^{S_{n}},\ldots,\mu_{m_n}^{S_{n}}\}\),\[n\in[N]\],\(\mu_{i}^{S_{n}},i\in[m_{n}]\)为\(\mathbf{x}_{i}^{S_{n}}\)的隶属函数。
\(\mathbf{R}_{S}^{M}=\{\mathbf{R}_{1}^{M},\mathbf{R}_{2}^{M},\dots,\mathbf{R}_{N}^{M}\}\)表示为\(\mathcal{S}\)上的模糊等价关系空间,其中,\(\mathbf{R}_{n}^{M},n\in[N]\),为\(S^n\)上的模糊等价关系。这里,\(\mathbf{R}_{n}^{M}\)是一个\(m_n\times m_n\)矩阵(详见[17]和[18]) \[({\bf R}_{n}^{M})_{i j}={\bf R}_{S_{n}}({\bf
x}_{i}^{S_{n}},{\bf
x}_{j}^{S_{n}};\mu_{i}^{S_{n}},\mu_{j}^{S_{n}}),\quad
i,j\in[m_{n}]\] 其中,\(R_{S_n}\)是\(S_n\)上的一个模糊等价关系算子。
因此,基于模糊等价的迁移学习框架旨在利用从\(\mathbf{D}=\{\mathcal{S},\mathcal{U},\mathbf{R}_{S}^{M}\}\)中获得的知识来拟合目标域内的数据。
B.模糊数据流学习
数据流学习[19],[20],也被称为流挖掘,指的是一组技术和算法,旨在处理和分析以流的方式持续到达的数据。然而,在现实世界的场景中,数据的统计属性可能会随着时间的推移而变化,这使得以前精确的模型和算法会随着时间的推移而失效。这种现象被称为概念漂移[21],[22],[23]。下面是概念漂移的正式定义。
定义1(概念漂移[23]):考虑一个时间段[0,t]和一组样本,记为\(S_{0,t} = \{d_0,...,d_t\}\),其中\(d_i=(X_i,y_i)\)是一个观察结果(或一个数据实例)。\(X_i\)是特征向量,\(y_i\)是标签,\(S_{0,t}\)遵循一定的分布\(\mathbb{F}_{0,t}(X,y)\)。当\(\mathbb{R}_{0,t}(X,y)\neq\mathbb{R}_{t+1,\infty}(X,y)\)时,在t+1时刻发生概念漂移,记为\(\exists
t:\mathbb{P}_{t}(X,y)\neq\mathbb{P}_{t+1}(X,y)\)。
因此,当概念漂移发生在t
+ 1时,我们的目标是调整预测\(H_{t}=\arg\operatorname*{min}_{h\in\cal
H}\ell(h,X,y|(X,y)\in\mathbb{P}_{t}(X,y))\)以适应新的分布Pt+1(X,y)。接下来,我们简要介绍了一个基于模糊聚类的漂移学习结构[24],来展示如何将模糊逻辑集成到数据流学习中。
C. 模糊强化学习
RL
[27]是在学习者(称为代理)主动与环境交互以实现特定目标的场景下进行计划和学习的研究。代理的目标是制定积累奖励的最佳策略。它通过从它接收到的反馈中学习来做到这一点。RL已经成功地应用于各种现实世界的问题,如机器人控制[28]、游戏玩[29]和自动驾驶[30]。在本节中,我们将提供关于如何将模糊逻辑集成到RL中的信息。
首先,模糊集可以用来表示RL中的状态、行动或奖励空间的不确定性。例如,模糊奖励信号[31]表示代理所接收到的奖励的不确定性或不精确性。此外,使用模糊逻辑将输入映射到控制动作的模糊控制器[32]可以集成到RL系统中,以处理不确定的或定性的控制决策。接下来,我们给出了一个模糊控制器的一般数学表达式。设X1,...,Xn为模糊控制器的输入变量,Y为表示控制动作的输出变量。与每个变量相关的模糊集表示为A1,...,An表示输入,B表示输出。设μAi(xi)表示输入Xi的模糊集Ai的隶属度函数,设μB
(y)表示输出Y的模糊集B的隶属度函数。然后,定义从输入到输出的映射的通用模糊规则可以表示为
\[{\mathrm{if}}\,X_{i}\,{\mathrm{i}}\,{\mathrm{k}}\,A_{1j}\,{\mathrm{~and}}\cdot\cdot\cdot\mathrm{and}\,X_{n}\,{\mathrm{is}}\,A_{n
j}\,,{\mathrm{then}}\,Y\,{\mathrm{is}}\,B_{j}\]
应用模糊规则后,进行去模糊化,得到一个清晰的输出值。
此外,模糊推理系统可以用于RL
[33]中的决策,例如基于代表不确定状态或奖励的模糊输入信号来确定下一步要采取的行动。例如,模糊q学习[34]扩展了q学习,通过结合模糊逻辑来处理不确定和不精确的状态-动作对。采用模糊规则和隶属度函数对q值进行了更新。
D. 模糊重组系统
III.模糊经典机器学习
经典的机器学习算法,如决策树、支持向量机(SVMs)和神经网络,在理论上和实践角度都取得了显著的成就。许多文章涉及到结合模糊技术与经典的机器学习算法,以克服不同类型的不确定性问题,如不完整的信息和不精确的观察。在本节中,我们总结了这些工作,并将这些技术分为两类: 1)基于非深度学习的方法和2)基于深度学习的方法。
A. 基于非深度学习的方法
B. 基于深度学习的方法
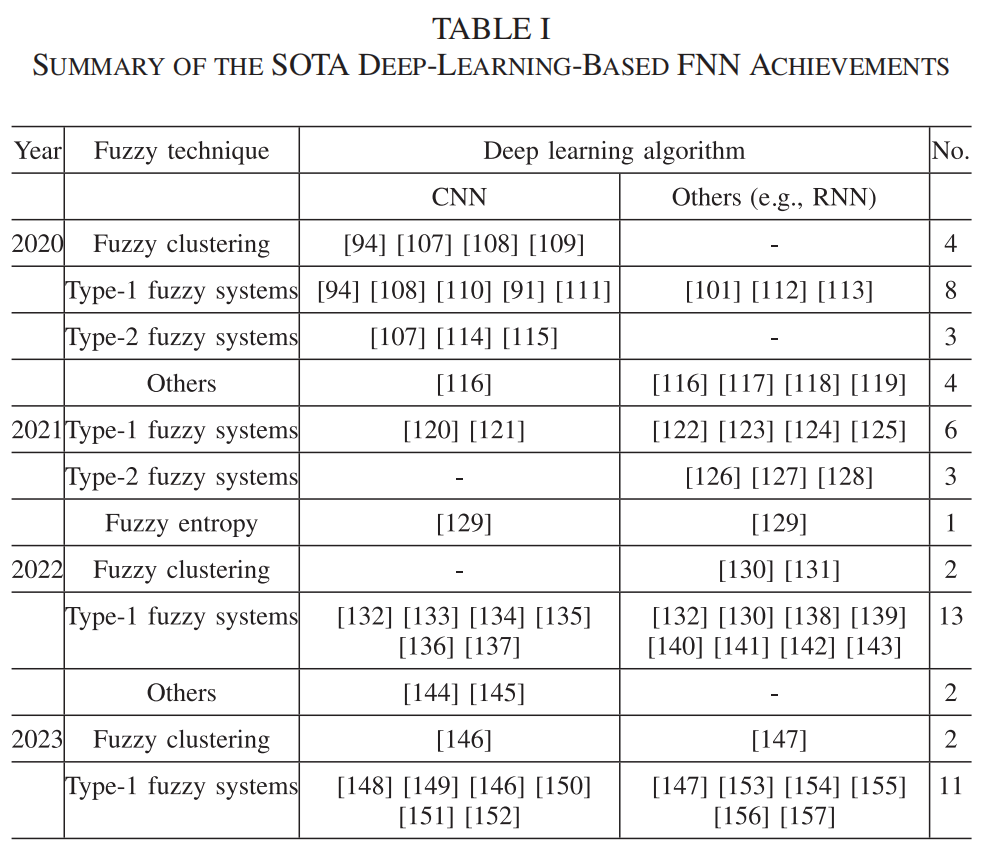
表一提供了与使用fnn的深度学习相关的SOTA文献的摘要。
IV. 模糊迁移学习
值得注意的是,大多数当前的迁移学习[158]方法在处理具有不确定性的真实情况时都有局限性,例如当只有少数标记实例可用时。为了克服这些问题,许多研究者已经转向了模糊集和模糊逻辑。
现有的关于迁移学习的研究可以根据正在转移的知识类型进行分类。这些知识类别包括实例[159]、特征表示[160]、模型参数[161]和关系知识[162]。另外,根据所解决的问题设置,研究可以分为四类:多任务学习[163]、领域适应[164]、[165]、跨领域适应[166]和异构学习[167]。基于所使用的模糊技术,我们将我们最近的工作(2015-2023年)的总结分为三个领域。这些都是模糊集、模糊系统和模糊关系。表二总结了模糊迁移学习领域的最新成果。