Robust deep k-means: An effective and simple method for data clustering

摘要

聚类的目的是根据一些距离或相似度度量将输入数据集划分为不同的组。k-means算法由于其简单、高效，是目前应用最广泛的聚类方法之一。在过去的几十年里，k-means及其各种扩展来解决实际的聚类问题。然而，现有的聚类方法通常采用单层公式（即浅层公式）。因此，所获得的低级表示与原始输入数据之间的映射可能包含相当复杂的层次信息。为了克服低层次特征的缺点，采用深度学习技术提取深度表示，提高聚类性能。在本文中，我们提出了一个鲁棒的深度k-means模型来学习与不同隐式低级属性相关的隐藏表示。通过使用深度结构分层地执行k-means，可以分层地利用数据的分层语义。来自同一个类的数据样本被迫逐层地靠近，这有利于聚类任务。我们的模型的目标函数被推导为一个更可跟踪的形式，这样优化问题可以更容易地解决，并可以得到最终的鲁棒结果。在12个基准数据集上的实验结果表明，与经典方法和最先进的方法相比，该模型在聚类性能方面取得了突破。

1.介绍

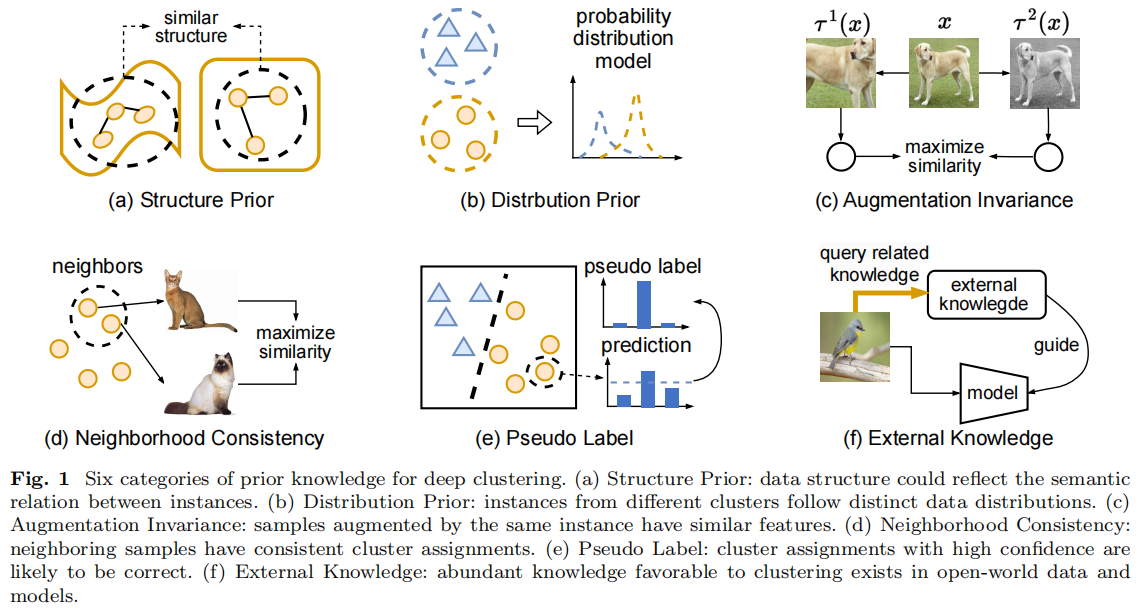
尽管上述k-means方法取得了显著的进展，但这些方法通常是用单层公式设计的。因此，所获得的低维表示与原始输入数据之间的映射可能包含相当复杂的层次信息。考虑到深度学习的发展，需要采用多个处理层来提取数据[29]的层次信息，本文提出了一种新的鲁棒深度k-means模型来利用多层次属性的层次信息。我们的模型的总体框架如图1所示。

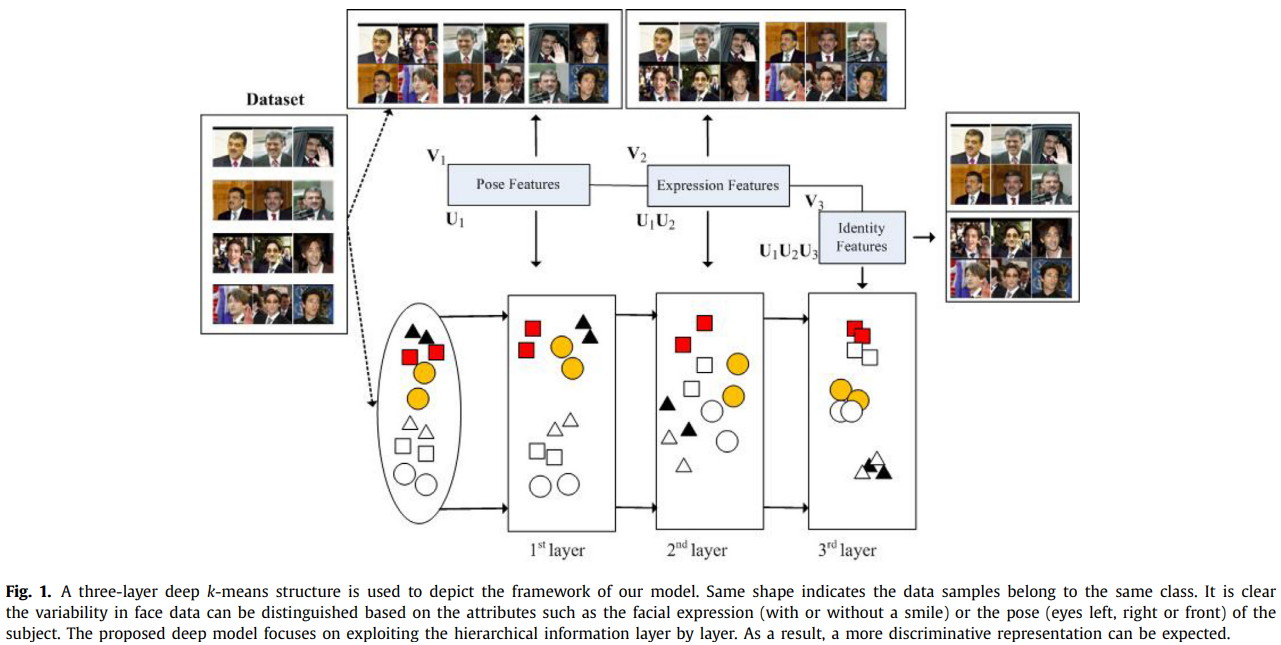
正如我们所看到的，通过使用深度结构来分层地执行k-means，数据的分层语义可以被分层地利用。也就是说，来自同一类的数据样本逐层地收集，非常有利于聚类任务。
这项工作的主要贡献有三个方面：

提出了一种新的鲁棒深度模型来分层地执行k-均值，从而可以分层地探索数据的分层语义。因此，来自同一类的数据样本可以有效地逐层收集，从而提供了一个清晰的聚类结构。
为了求解模型的优化问题，将相应的目标函数推导为更可跟踪的形式，并提出了一种替代的更新算法来求解优化问题。
在12个基准数据集上进行了实验，并显示了与经典和最先进的方法相比的良好结果。

本文的基础构思如下。我们将在第2节中简要介绍与密切相关的工作。我们的模型的细节见第3节。实验结果见第4节。最后，我们在第5节中给出了本文的结论。

这项工作和我们早期的论文[1]之间有三个不同之处。
首先，我们提出了鲁棒深度kkmeans模型的一般形式。详细地说，我们部署了一系列的散度函数来测量重构误差（第3节），而不仅仅是对噪声数据和异常值敏感的Frobenius范数。因此，我们早期的工作[1]只是本文的一个特例。其次，在12个基准数据集上进行了更全面的实验，验证了我们模型的鲁棒性和有效性： (i)记录了更多数据集和高级基线上的聚类结果（第4.3节）；（ii）添加不同参数设置的实验结果（第4.4节）；（iii）展示收敛分析实验（第4.5节）；（iv）研究不同发散函数对聚类性能的影响（第4.6节）。第三，我们介绍了更密切相关的文献（在第1节和第2节中），澄清了它们与最先进的技术之间的联系和差异。这有助于在社区中更好地定位拟议的工作。

2.前期准备工作

非负矩阵分解（NMF）由于其直观的基于部分的解释[30,31]，在数据聚类中受到了广泛的关注。以往的研究表明，在松弛条件[30]下，NMF基本上等于k-means。假设$\mathbf{X}=\left[\mathbf{x}_{1},\mathbf{x}_{2},\ldots,\mathbf{x}_{n}\right]\in\mathbb{R}^{m\times n}$是一个具有n个数据样本和m个特征的非负数据矩阵。NMF的目标是找到两个非负矩阵$\mathbf{U}\in\mathbb{R}^{m\times c}$和$\mathbf{V}\in\mathbb{R}^{n\times c}$，使$\mathbf{X}\approx\mathbf{UV}^{T}$，NMF的一般形式为 $$ \[\begin{array}{l} {\cal D} _{\beta} (X|\mathrm{UV}^{T}\bigr)= \sum_{i=1}^{m} \sum_{j=0}^{n} d_{\beta}(X_{i j}|igl(\mathrm{U}^{T}\bigr)_{i j}\bigr)\\ {s.t.{\bf U}\geq0,{\bf V}\geq0,}\end{array}\]

$$ 其中${\mathcal{D}}_{\beta}(\mathbf{X}|{\hat{\mathbf{X}}})$表示一个标量代价函数（即$\mathbf{X}$与其重建$\hat{\mathbf{X}}$之间的一些发散度量），$\mathbf{X_{ij}}$是$\mathbf{X}$的第$ij$个元素。在公式(1)，可以采用一类称为β-散度[33]的散度函数。在NMF中使用最广泛的有三个散度函数：

∗β=2（欧氏距离）：$d_{2}(a|b)={\frac{1}{2}}(a-b)^{2}$
∗β=1（Kullback–Leibler Divergence）：$d_{1}(a|b)=a\log{\frac{a}{b}}-a+b$
*β=0（Itakura–Saito Divergence）：$d_{0}(a|b)=\frac{a}{b}-\log{\frac{a}{b}}-1$

[32]采用了等式(1)中的欧氏距离： \[\begin{array}{l} {J_{N M F}=\sum_{i=1}^{m}\sum_{i=1}^{n}\left(X_{i j}-({\bf U}V^{T})_{i j}\right)^{2}=\|{\bf X}-{\bf U}V^{T}\|_{F}^{2}}\\ {s.t.{\bf U}\geq0,{\bf V}\geq0,}\end{array}\] 其中，$\|\cdot\|_{F}$表示Frobenius范数。[32]进一步指出，等式(2)是一个双凸公式（仅在U或V中为凸），并通过应用更新规则搜索局部最小值如下：

$\mathbf{U}_{i j}\leftarrow \mathbf{U}_{i j} \frac{(\mathbf{X V})_{i j}}{(\mathbf{U V ^{T} V})_{i j}}$， $\mathbf{V}_{i j}\leftarrow \mathbf{V}_{i j} \frac{(\mathbf{X U^{T}})_{i j}}{(\mathbf{V U ^{T} U})_{i j}}$

其中，$\mathbf{V}$可以看作是聚类指标矩阵[30]，$\mathbf{U}$表示质心矩阵，c表示聚类数。通常，我们有$c\ll n$和$c\ll m$，意思是等式(2)实际上是搜索$\mathbf{X}$的低维表示$\mathbf{V}$。
但在现实中，数据集通常是复杂的，并且总是包含多种层次模式（即因素）。以人脸数据集为例，它通常由一些常见的模式组成，如表达式、姿态、场景等。因此，很明显，基于单层的NMF不能充分利用不同因素下的隐藏信息。为了填补这一空白，[34]研究了一个多层深度模型，该模型通过进行semi-NMF的分层处理，创新性地探索了数据的分层信息。并定义了深度semi-NMF模型的基本公式为 \[\begin{array}{r l}{X}&{\approx U_{1}V_{2}^{T},}\\ {X}&{\approx U_{1}U_{2}V_{2}^{T},}\\ &{\vdots}\\ {X}&{\approx U_{1}U_{2}\dots{U}_{r}V_{r}^{T}.}\end{array}\] 其中r为层数，$\mathbf U_i$和$\mathbf V_i$分别为第$i$个层的基矩阵和表示矩阵。很明显，深度semi-NMF的目标也是搜索一个低维的嵌入表示，即最后一层$\mathbf V_r$。通过分层分解每个层$\mathbf{V}_{i}(i\lt r)$，等式(3)能够发现潜在的层次结构。与现有的单层NMF模型相比，深度semi-NMF可以更好地揭示数据的层次信息，因为不同层的低维表示可以识别出不同的模式。因此，我们的模型可以完全实现适合后续不同模式聚类的表示。例如，如图1所示，$\mathbf U_3$对应于表达式的特征，$\mathbf {U_2U_3}$对应于姿态的特征，最后，$\mathbf {U=U_1U_2U_3}$对应于人脸图像的身份映射。这样，就可以获得更好的高可识别性、根据变异性最小的特征进行聚类的最终层表示。

3.提出的模型

在本节中，我们提出了一种新的深度k均值模型，称为鲁棒的深度k-means（RDKM）。我们提出了一种有效的更新算法来解决相应的优化问题。并分析了该算法的收敛性。

3.1.鲁棒的深度k-means

为了探索不同模态的低维表示，研究了一种新的鲁棒深度k-means模型，利用深度结构分层进行k-means。在本文中，为了扩大我们的模型的适用范围（即同时处理负数据和非负数据），我们省略了对$\mathbf U_i$的非负约束。考虑到$V_i$上的非负性约束使优化问题难以解决，我们通过引入新的变量$V_i^+$，将目标函数转化为更可跟踪的形式。这样，非负性约束条件被分离并等价地采用，约束条件为$V_i=V_i^+$。因此，我们不仅扩展了应用程序，而且还保留了我们的模型的强可解释性。这里我们使用乘子（ADMM）[35]的交替方向方法来求解优化问题。在数学上，所提出的RDMK模型被表述为 \[\begin{array}{l} {J=D_{\beta}(\mathbf{X}|\mathbf{Y})}\\ {\mathrm{s.t.}}\mathbf{Y}=\mathbf{U}_{1}\mathbf{U}_{2}\ldots\mathbf{U}_{r}\mathbf{V}_{r}^{T},(\mathbf{V}_{r})_{.c}=\{0,1\},\sum_{c=1}^{C}\,(\mathbf{V}_{r})_{.c}=1,\\ {\mathbf{V}_{i}=\mathbf{V}_{i}^{+},\mathbf{V}_{i}^{+}\geq0,i\in[1,\ldots,r-1].}\end{array}\] 在等式(4)中，我们可以看到在$\mathbf{V}_{r}$的每一行上都采用了1-of-C的编码方案。1-of-C编码方案的主要目标是保证$\mathbf{V}_{r}$的唯一性。此外，基于$\mathbf{V}_{r}$，我们可以直接得到最终的离散划分结果。
类似于等式(2)，如果在等式(4)中采用欧氏距离（即β = 2），则我们有 \[\begin{array}{l} {J=\|\mathbf{X}-\mathbf{Y}\|_{F}^{2}}\\ {\mathrm{s.t.}}\mathbf{Y}=\mathbf{U}_{1}\mathbf{U}_{2}\ldots\mathbf{U}_{r}\mathbf{V}_{r}^{T},(\mathbf{V}_{r})_{.c}=\{0,1\},\sum_{c=1}^{C}\,(\mathbf{V}_{r})_{.c}=1,\\ {\mathbf{V}_{i}=\mathbf{V}_{i}^{+},\mathbf{V}_{i}^{+}\geq0,i\in[1,\ldots,r-1].}\end{array}\] 然而，已经证明了Frobenius范数对噪声数据和异常值[36,37]很敏感。为了提高该模型的鲁棒性，我们的模型采用了稀疏性诱导范数（即$l_{2,1}$范数）。根据[36]，$l_{2,1}$范数能够减少异常值的影响，因为它在数据点内执行$l_{2}$范数，在数据点之间执行$l_{1}$范数。最后，我们的鲁棒深度k-means（RDKM）模型被写为 \[\begin{array}{l} {J_{RDKM}=\|\mathbf{X}-\mathbf{Y}\|_{2,1}}\\ {\mathrm{s.t.}}\mathbf{Y}=\mathbf{U}_{1}\mathbf{U}_{2}\ldots\mathbf{U}_{r}\mathbf{V}_{r}^{T},(\mathbf{V}_{r})_{.c}=\{0,1\},\sum_{c=1}^{C}\,(\mathbf{V}_{r})_{.c}=1,\\ {\mathbf{V}_{i}=\mathbf{V}_{i}^{+},\mathbf{V}_{i}^{+}\geq0,i\in[1,\ldots,r-1].}\end{array}\] 正如我们所看到的，$\|\mathbf{X}-\mathbf{Y}\|_{2,1}$相对于Y很容易最小化，而$\|\mathbf{X}-\mathbf{U}_{1}\mathbf{U}_{2}\ldots\mathbf{U}_{r}\mathbf{V}_{r}^{T}\|_{2,1}$相对于$\mathbf U_i$或$\mathbf V_i$来最小化并不是那么简单。乘法更新规则隐式地解决了$\mathbf U_i$和$\mathbf V_i$解耦的问题。在ADMM背景下，一个自然的公式是优化$\|\mathbf{X}-\mathbf{Y}\|_{2,1}$，约束条件为$\mathbf{Y}=\mathbf{U}_{1}\mathbf{U}_{2}\ldots\mathbf{U}_{r}\mathbf{V}_{r}^{T}$。这就是我们考虑解决方程式（6）这样的问题的原因。
为了验证在我们的模型中使用的$l_{2,1}$范数的鲁棒性和有效性，不同的散度函数（即，β = 2，β = 1，和β = 0）的情况将在后面的章节中讨论。关于不同发散函数的优化算法也将在附录A中描述。
对于等式(6)，提出了一种基于ADMM [35]的有效优化算法。等式(6)的拉格朗日函数是 \[\mathcal{L}(\mathbf{Y},\mathbf{U}_{i},\mathbf{V}_{i},\mathbf{V}_{i}^{+},\mathbf{\mu,\lambda_{i})}=\|\mathbf{X}-\mathbf{Y}\|_{2,1}+\langle\mu,\mathbf{Y}-\mathbf{U}_{1}\mathbf{U}_{2}\dots\mathbf{U}_{r}\mathbf{V}_{r}^{T}\rangle\\+\,{\frac{\rho}{2}}\,\|\mathbf{Y}-\mathbf{U}_{1}\mathbf{U}_{2}\ldots\mathbf{U}_{r}\mathbf{V}_{r}^{T}\|_{F}^{2}+{\sum_{i=1}^{r-1}\left\langle\lambda_{i},\mathbf{V}_{i}-\mathbf{V}_{i}^{+}\right\rangle}+\frac{\rho}{2}\sum_{i=1}^{r-1}\|\mathbf{V}_{i}-\mathbf{V}_{i}^{+}\|_{F}^{2},\] 其中$\rho$为一个惩罚参数，$\mu$和$\lambda_i$均表示拉格朗日乘子，而$\langle\cdot,\cdot\rangle$表示内积运算。

3.2.最优化

3.3.收敛性分析

4.实验

在本文中，我们通过实验评价了该方法的有效性。我们将12个基准数据集上的RDKM与6个基线进行比较：标准-NMF（SNMF）[38]，-均值[8]，NMF [32]，正交NMF（ONMF）[30]，半2,1-NMF[36]和深度半NMF（DeepSNMF）[34]。

4.1.数据集

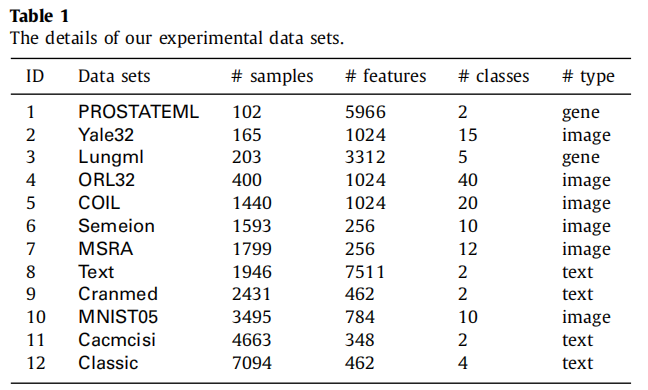
在我们的实验中，我们采用了12个基准数据集，包括2个基因表达数据集，4个文本数据集和6个图像数据集。如图所示，图2显示了数据集COIL和MNIST的样本图像。表1总结了所有数据集的具体细节，从中我们可以看到实例数量在102到7094之间，特征数量在256到7511之间，涵盖了广泛的属性。

4.2.参数设置

对于k-means算法，在所有数据集上进行k-means直到收敛。为了进行公平的比较，k-means的结果也被用作其他比较方法的初始化。对于比较的方法，我们设置的参数与每一篇论文中报告的一样。如果没有建议的值，我们将详尽地搜索参数，并使用产生最佳性能的参数。对于我们的RDKM，根据[14,39]，图层的大小（如3.2中所述）被设置为[50 C]、[100 C]和[100 50 C]。对于参数ρ，我们从{1e5、1e4、1e3、1e2、0.1、1、10、100}中搜索它。为了减少初始化的影响，我们重复了20次实验，并报告了20次重复的平均性能。

4.3.结果及分析

表2显示了12个数据集上所有方法在聚类精度（ACC）、归一化互信息（NMI）和纯度等方面的聚类性能。

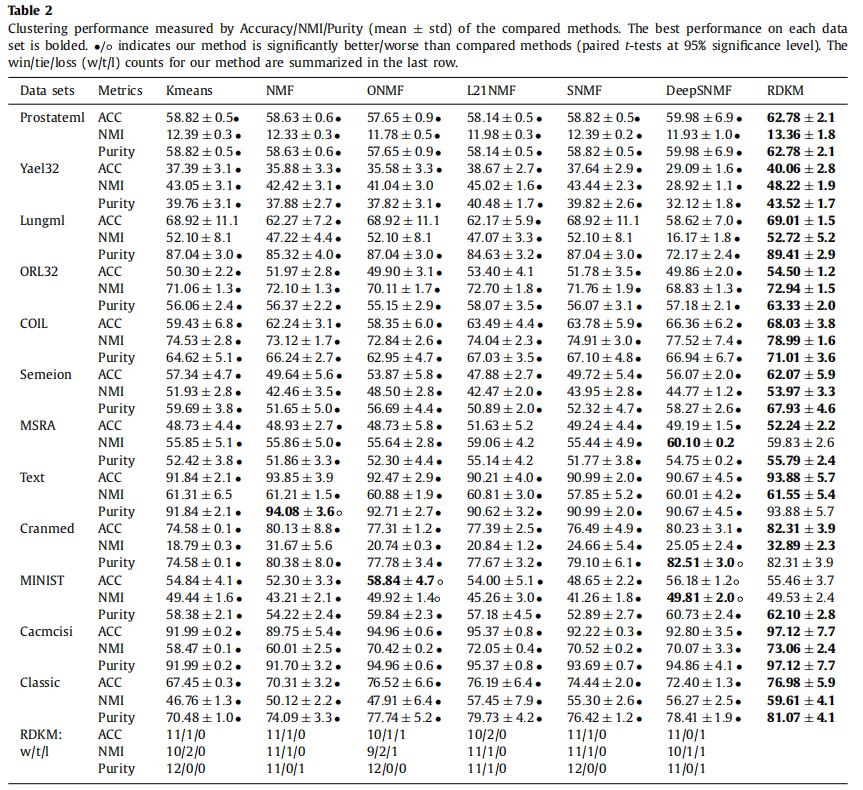
可以看出，该方法在大多数情况下都优于其他算法。具体来说，对于ACC，我们的模型在12个数据集中获得了11倍的最佳结果。对于NMI，我们的模型达到了10次的最佳结果。对于纯度，这个数字也是10。总之，其聚类性能足以验证所提模型的有效性。RDKM的优越性表明，通过探索数据的层次语义来发现更好的集群结构是有益的。其原因是，通过应用深度框架进行k-means的分层执行，可以分层利用数据的分层信息，最后为聚类任务获得更好的高可识别性、最终层表示。通过巧妙地结合深度框架和k-means模型，我们的模型能够在一般情况下提高聚类性能。
根据本文报道的理论分析和实证结果，可以看出，将深度结构学习和经典机器学习模型结合成一个统一的框架将是一个有趣的研究趋势。

4.4.参数讨论

在我们的模型中，有两个参数，图层大小和惩罚参数ρ，需要进行调整。在这里，我们研究了在不同的参数设置下的聚类性能。如图3所示，我们可以发现聚类性能对于不同的层大小设置是稳定的，而性能对惩罚参数ρ有点敏感。对于图像数据集（如Yale32、ORL32、COIL和MSRA），当ρ在[1e3,1e1]范围内时，可以得到更好的结果。对于基因表达数据集（如Lungml），当ρ在该范围内时，可以获得更好的结果[1e2,1]。而对于文本数据（例如，Cranmed），在[1e5,1e3]范围内搜索ρ将是一个更好的选择。一般来说，我们可以在[1e3,1]范围内搜索参数ρ，以获得相对较好的性能。

4.5.收敛性分析

在本小节中，我们通过经验展示了我们的方法收敛的速度。图4为我们的RDKM的收敛曲线，其中x轴为迭代次数，y轴为目标值。可以观察到，我们的RDKM的更新规则收敛得非常快，通常在100次迭代内。对于数据集MSRA，它甚至在10次迭代内收敛，进一步证明了所提出的优化算法的有效性。

4.6.散度函数的选择

如第2节所述，可以采用几种广泛使用的散度函数来进行残差计算。我们在之前的实验中使用了l2,1-范数。在本节中，我们通过实证研究了不同的发散函数对聚类性能的影响。从方程式(6)和(7)中可以看出，当散度函数发生改变时，只有更新Y的步骤才会发生改变。也就是说，对于不同的发散函数，除Y之外的所有变量的更新都是相同的。在附录A中给出了β=2（欧几里得距离）、β=1（库背-莱布勒发散）和β=0（岩仓-斋藤发散）时的更新规则。
对不同散度函数的聚类性能如图5所示。为了进行比较，我们还记录了我们的模型（即基于12,1-范数的发散函数）的结果。很明显，l2,1-norm在所有数据集上都优于其他发散函数，这再次验证了我们的模型的鲁棒性。对于β = 2、β = 1和β = 0这三种情况，我们可以看到β = 1在数据集Yale32上获得了良好的结果，β = 0在数据集Lungml上获得了良好的结果，而β = 2在数据集ORL32和COIL上取得了更好的结果。也就是说，不同的散度函数在不同的数据集上得到更好的结果。一般来说，l2,1-norm可能是一个更好的选择，因为它始终取得良好的性能。

5.结论

在本文中，我们引入了一个鲁棒的深度k-means模型来学习具有不同隐式低级属性的隐表示。通过使用深度结构分层地执行k-means，可以分层地利用数据的分层语义。来自同一个类的数据样本被迫逐层地靠近，这有利于聚类任务。我们的模型的目标函数被推导为一个更可跟踪的形式，这样优化问题可以更容易地解决，并可以得到最终的鲁棒结果。超过12个基准数据集的实验结果表明： (i)与经典和最先进的方法相比，该模型在聚类性能方面取得了突破；（ii）聚类性能对不同的层大小设置和发散函数的聚类性能具有鲁棒性；（iii）提出的优化算法有效，收敛速度快。在我们未来的工作中，将我们的深度模型和其他机器学习模型（例如，内核学习和分类方法）结合到一个统一的框架中将是很有趣的。