Stacking Brick by Brick:Aligned Feature Isolation for Incremental Face Forgery Detection

Stacking Brick by Brick: Aligned Feature Isolation for Incremental Face Forgery Detection

Jikang Cheng1*, Zhiyuan Yan 2*, Ying Zhang3, Li Hao2, Jiaxin Ai1, Qin Zou1, Chen Li3, Zhongyuan Wang1†

武汉大学计算机学院1
北京大学深圳研究生院电子与计算机工程学院2
微信视觉，腾讯公司3

摘要

​  随着面部伪造技术的快速发展，出现了越来越多种类的伪造。增量式面部伪造检测（Incremental face forgery Detection，IFFD）通过逐步添加新的伪造数据来微调已训练的模型，被引入作为应对不断演变的伪造方法的一种有前景的策略。然而，一个未经充分训练的IFFD模型在处理新的伪造时容易出现灾难性遗忘。这是因为将所有伪造都视为单一的“假”类别，导致不同类型的伪造品相互覆盖，从而导致早期任务中独特特征的遗忘，限制了模型在学习伪造品特异性和普遍性方面的有效性。在本文中，我们提出了一种方法，通过将先前任务和新任务的潜在特征分布逐块堆叠，实现特征的对齐隔离。这样做的目的是保留已学习到的伪造信息，并通过最小化分布重叠来积累新知识，从而减轻灾难性遗忘。为了达到这一目标，我们首先引入了稀疏均匀回放（SUR），以获取可以视为先前全局分布的均匀稀疏版本的代表性子集。接着，我们提出了一个潜在空间增量检测器（LID），该检测器利用SUR数据来隔离和对齐分布。为了评估我们的方法，我们构建了一个更先进、更全面的基准测试，专门针对IFFD。实验结果证明了我们方法的优越性。代码可在https://github.com/beautyremain/SUR-LID上获取。

Incremental Face Forgery Detection: A New Approach - Simple Science

1.引言

​  随着人脸伪造技术的兴起，社会面临重大威胁，这引起了研究者们的高度关注，他们特别关注这些技术在身份盗用、虚假信息传播和隐私侵犯方面的潜在风险。因此，开发有效的检测方法对于保护个人安全和维护公众对数字互动的信任至关重要。现有的方法主要集中在使用有限的训练数据来训练通用的面部伪造检测器。然而，随着现实世界中面部伪造技术的日益多样化，仅依赖有限的训练数据期望通用模型能够有效检测所有类型的伪造，这显得有些不切实际[4]。与此同时，每当出现新的伪造品时，使用所有可用数据训练新模型会导致计算费用、存储限制和隐私影响的重大问题。因此，考虑到伪造数据量的不断增加，采用增量学习研究范式进行人脸识别检测可以解决更广泛的应用场景。
​  迄今为止，只有少数方法探索了增量面部伪造检测（IFFD）[19,30,39,41]领域。这些方法通过多种重放策略来保留先前任务中的代表性信息，例如选择中心样本和困难样本[30]、生成代表性的对抗性扰动[39]以及考虑混合原型[41]。然而，由于IFFD始终致力于学习同一简单的二分类任务，骨干提取器更容易随意用新生成的特征覆盖前一任务的全局特征分布。这种情况下，IFFD中的灾难性遗忘问题尤为突出。尽管目前的方法提出了多种重放和正则化策略，但这些方法主要集中在保留一些特定的代表性样本（例如DFIL[30]中的中心样本和困难样本），并保持这些样本的特征一致性。因此，这些方法难以维持和组织之前学习到的全局特征分布，从而难以缓解分布覆盖的问题。
​  在本文中，我们提出了一种方法，通过在潜在空间中逐块堆叠先前任务和新任务的特征分布，实现特征的对齐隔离。如图1所示，我们用“砖块”来描述这些特征分布，因为它们被设计为相互独立，而不是相互覆盖。而“逐块”则意味着逐步将新任务的二元决策边界与所有先前任务的边界对齐。实施‘逐块堆叠’方法的优势体现在两个方面。首先，通过特征隔离，可以减少新旧领域之间的特征分布重叠，从而更好地保留从前任务中获得的知识。其次，逐个决策对齐确保了在增量学习过程中，能够有效利用累积的多样化伪造信息，进行最终的二进制面部伪造检测。
​  为了实现特征的对齐隔离，我们提出了一种新的IFFD方法，称为SUR-LID。具体来说，为了对齐和隔离所有特征分布，一个先决条件是获取能够代表先前全局分布的重放子集。因此，我们首先提出了一个基于稳定性和分布密度选择重放样本的稀疏均匀重放（SUR）策略。SUR子集的分布可以视为原始全局分布的均匀稀疏版本。借助SUR算法保持的分布特性，我们提出了一种潜在空间增量检测器（LID），以实现特征的对齐隔离。该检测器通过隔离损失来隔离每个分布，并通过重新填充分布的方式进一步增强效果，从而基于SUR数据恢复并模拟之前的全局分布。随后，引入了增量决策对齐机制，确保新任务的决策边界与所有先前任务保持一致。此外，我们还设计了两种精心设计的增量协议，以提升IFFD性能的实验评估。初步结果证明了所提方法的优越性。我们的贡献可以概括为：

• 我们提出在潜在空间中，将先前任务与新任务的特征分布逐层叠加，实现特征对齐隔离。这种方法既能缓解特征覆盖问题，又能有效整合学习到的多样化伪造信息，从而提升面部伪造检测性能。
• 为了实现特征的对齐隔离，我们引入了SUR来存储之前的全局分布和LID，并利用SUR数据来实现特征的隔离和对齐。
• 我们精心构建了一个新的综合评估IFFD的基准，包括多种最新的伪造方法和两种与实际应用相关的协议。

2.背景

2.1 IFFD的初步情况

​  训练范式
​  在增量学习中，新数据会依次引入，以微调已经基于先前任务训练好的模型，而完整的先前数据则无法访问[8]。与从头开始使用所有可用数据重新训练模型相比，这种范式能够逐步利用新数据，同时减少计算开销和存储需求。

​  研究目的
​  在[39]的基础上，我们旨在解决增量学习中的灾难性遗忘问题，即在增加新任务时，模型对先前学习任务的性能可能会显著下降，也就是遗忘已学知识。

​  重放集
​  重放集指的是从已学习的训练集中存储一小部分数据。它在几乎不增加额外存储开销的情况下，能够显著提升模型保留先前学习知识的能力，同时为增强增量学习提供了设计灵活性。

2.2 面部伪造检测器

​  现有的方法主要集中在检测器的泛化上，以应对面部伪造带来的严重威胁。例如，鉴于检测器中观察到的模型偏差，已经提出了多种方法[5,23,44]来减轻伪造样本中存在的模型偏差。在潜在空间中，也有方法[4,46]研究特征组织和融合，以挖掘和多样化伪造信息，从而提高通用伪造检测器的泛化能力。这些方法[4-6,13,15,23,24,44,46]旨在从有限的已知数据中提取通用伪造信息，并在少量未知数据中展现出良好的性能。
​  然而，考虑到面部伪造技术的快速发展，仅凭有限的可见数据来训练理想的通用检测器是不切实际的。因此，增量学习模式可能成为适应多样化和不断演变的伪造技术的更优选择。

2.3 增量式人脸伪造检测

​  增量学习方法被广泛研究，主要分为参数隔离[8]、参数正则化[1,20,22]和数据重放[26,31]。然而，专注于构建有效框架以实现增量面部伪造检测的方法却不多。CoReD [19]通过蒸馏损失来保留先前任务的知识，而DFIL [30]则通过使用中心样本和困难样本进行重放，进一步增强了这一功能。HDP [39]将通用对抗扰动（UAP [28]）作为重放机制，用于获取早期任务的知识。DMP [41]利用混合原型创建重放集，以封装先前的任务。
​  尽管现有的方法能够重放并维护来自少数代表性数据（如中心样本和困难样本）的知识，但它们无法维持和组织先前任务与新任务的全局分布。因此，先前的全局分布经常被新任务的分布所覆盖，导致遗忘问题，以及对伪造特异性和普遍性的学习不足。

3.方法论

3.1.对齐特征隔离的原理

​  在训练过程中，骨干提取器学会了将图像空间的输入映射到潜在空间中的代表性特征（即图像-特征映射）。因此，提取出的特征的全局分布能够反映出骨干提取器从训练任务中学到的知识。如果覆盖了之前的分布，可能会破坏之前学到的图像-特征映射，从而导致遗忘先前任务中的知识。此外，研究表明，潜在空间的组织对于模型的有效性至关重要[4,7,11]。现有的方法[19,30,39,41]虽然能够保留少数代表性数据点，但只能在这些特定点上保持性能，而无法维持全局分布。同时，在不保留全局分布的情况下，组织先前和新任务的潜在空间也是一项挑战。
​  因此，我们提出了一种对齐特征隔离的方法，以通过三个步骤来改进IFFD：
​  1)存储能够代表全局分布而非仅限于少数特定点的重放子集。
​  2)隔离每个任务的全局分布，以减少覆盖，从而允许逐步积累更加多样化的伪造信息。
​  3)利用通过决策对齐从隔离中获得的累积伪造信息，从而增强最终的二进制面部伪造检测。

3.2.总体框架

​  本文提出了一种针对IFFD的对齐特征隔离方法，该方法包含两个核心组件：一种名为稀疏均匀重播（SUR，Sparse Uniform Replay）的重播策略，以及一个名为潜在空间增量检测器（LID，Latent-space Incremental Detector）的检测模型。在完成某一任务的训练后，我们使用SUR来存储数据。随后，将SUR数据与下一个训练集合并，以训练LID进行增量面部伪造检测。整个框架如图2所示。

image-20250702160852295

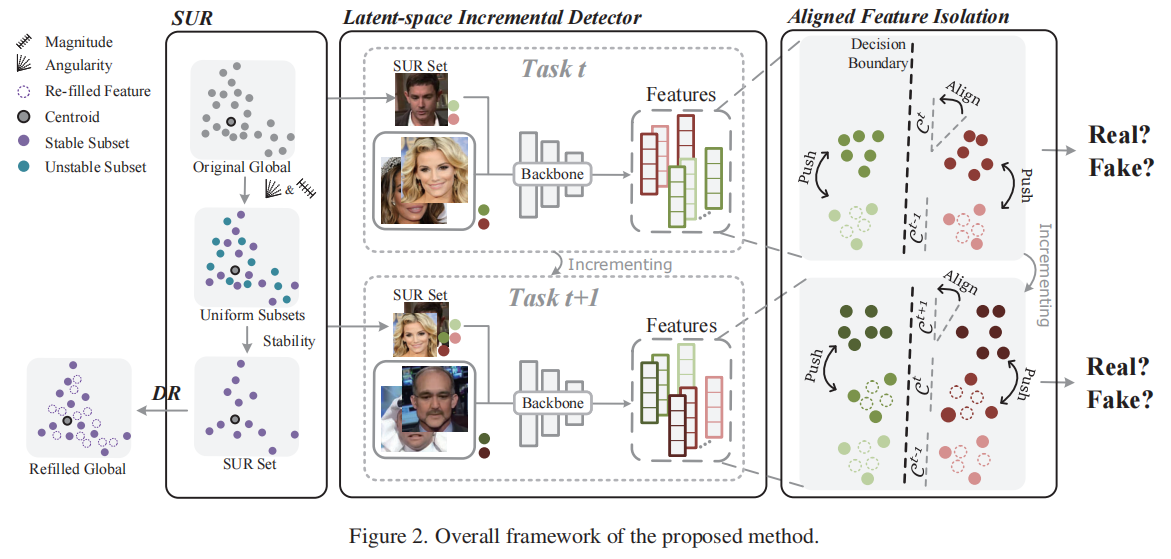
3.3.稀疏均匀重放(SUR，Sparse Uniform Replay)

​  为了实现所提出的对齐特征隔离，一个关键的前提是在增加新的（t+1）任务时，需要参考前t个任务的全局特征分布。因此，如图3所示，我们提出了稀疏均匀重放（SUR）策略，该策略旨在从先前的训练集中选择具有高维均匀性的稳定表示。（稳定表示指的是当输入中的无关内容发生[35,48]变化时，所提取的特征保持一致。）

image-20250702211733301

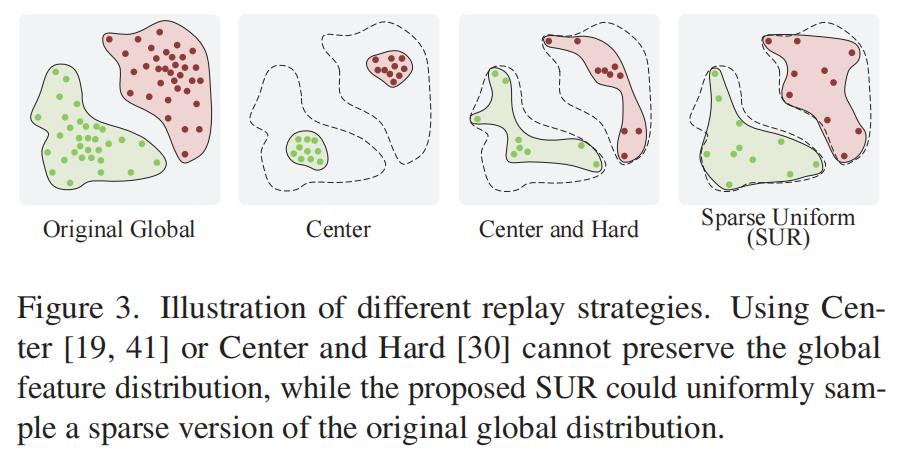
​  具体来说，保持重播集的均匀性可以使其更接近全局分布，而不仅仅是原始分布中的局部区域。同时，通过采样这些稳定提取的特征，可以减少重播集中包含异常值的风险。
​  考虑到一个任务通常包含真实和虚假的领域，为了简化符号表示，我们使用\(\mathbf{F}^{t}\in\mathbb{R}^{n\times d}\)和\(\mathbf{X}^{t}\in\mathbb{R}^{n\times 3\times w\times h}\)来表示特征的一个特定领域及其对应的图像，这些图像在第t个任务中可能是真实的或虚假的。其中，n表示样本数量，d表示特征的维度，w和h分别表示图像的宽度和高度。对于第t个任务\({\mathcal{E}}^{t}\)的训练好的骨干提取器，\(\mathbf{F}^{t}\)可以通过\(\mathbf{F}^{t}={\mathcal{E}}^{t}(\mathbf{X}^{t})\)生成。首先，我们利用质心作为参考，均匀地从重放集中采样，计算方法为\(\mathbf{c}^{t}=avg(\mathbf{F}^{t})\in\mathbb{R}^{d}\)。在高维特征空间中均匀采样时，需要同时考虑幅度和角度。具体来说，从\(\mathbf{c}^{t}\)到\(\mathbf{F}^{t}\)中每个特征的幅度可以表示为： \[{\mathbf M}^{t}=\|\mathbf{F}^{t}-\mathbf{c}^{t}\|_{2},\] ​  其中\(\|\ast\|_2\)表示计算欧几里得范数。随后，高维角矩阵\(\mathbf{A}^{t}\)可按以下方式计算： \[\mathbf{A}^{t}={\frac{(\mathbf{F}^{t}-\mathbf{c}^{t})}{||\mathbf{F}^{t}-\mathbf{c}^{t}||_{2}}}.\] ​  随后，我们利用无论是否打乱都存在的一致性[5,29,38]来量化学习到的表示的稳定性。也就是说，由于伪造信息主要是细粒度的，并且不受打乱的影响，因此无论是否打乱都存在，伪造特征应该是一致的[5,29,38]。因此，我们对\(\mathbf{X}^{t}\)执行网格洗牌[2]操作生成\(\mathbf{\tilde X}^{t}\)，从而获得洗牌数据的特征\(\mathbf{\tilde F}^{t}={\mathcal{E}}^{t}(\mathbf{\tilde X}^{t})\)。因此，稳定性矩阵\(\mathbf{S}^{t}\)中的第i个元素\((s_i^t)\)是通过使用\(\mathbf{\tilde F}^{t}\)和\(\mathbf{F}^{t}\)的第i个特征（\(\tilde f_i^t\)和\(f_i^t\)）来计算得出的： \[s_{i}^{t}={\frac{\tilde f_i^t\cdot(f_i^t)^{\mathrm{T}}}{\|\tilde f_i^t\|_{2}\cdot\|f_i^t\|_{2}}},\] ​  其中上标T表示转置矩阵。直观来说，为了获得统一且稳定的表示，这三个因素（即\(\mathbf{M}^{t}\in\mathbb{R}^{n}\)、\(\mathbf{A}^{t}\in\mathbb{R}^{n\times d}\)和\(\mathbf{S}^{t}\in\mathbb{R}^{n}\))应同时考虑以获得均匀和稳定的表示。然而，实现一个理想的策略需要高维线性规划，它乘法考虑所有三个矩阵来决定最佳的重放集，从而导致不可接受的复杂计算。在此，我们提出了一种近似算法，该算法能够识别每个矩阵段内的局部最优数据点，并将所有三个因素以加法方式综合考虑，从而显著降低计算量。具体来说，设每个域的重放集大小为\(n_r\)，我们首先根据幅度距离\(\mathbf{M}^{t}\)将\(\mathbf{F}^{t}\)按升序排列。接着，我们将\(\mathbf{F}^{t}\)分割成\(\frac{n_r}{2}\)个等长的段，每个段的长度为\(\mathbf{F}^{t}=\{\mathbf{F}^{t}_{1:\frac{2n}{n_r}},...,\mathbf{F}^{t}_{(n-\frac{2n}{n_r}):n}\}\in\mathbb{R}^{\frac{n_r}{2}\times \frac{2n}{n_r}\times d}\)。在每段内，我们根据\(\mathbf{S}^{t}\)识别出最稳定的特征\(f_s^t\)，并将其对应的图像\(x_s^t\)纳入重放集。为了同时考虑角度的均匀性（即\(\mathbf{A}^{t}\) )，我们在每个段中寻找与\(f_s^t\)具有最低归一化余弦相似度的特征，称为\(f_a^t\)。随后，我们可以从所有段中选择n个\(f_s^t\)和\(f_a^t\)。这些特征对应的图像被存储起来，构成一个领域（真实或假）的第t个重放集。补充材料中提供了SUR算法的简要总结。

3.4.潜空间增量探测器（LID，Latent-space Incremental Detector）

​  我们提出了一种潜在空间增量检测器（LID），该检测器在潜在空间中逐块堆叠先前和新的任务。LID包含两个关键要素：特征隔离和增量决策对齐。

3.4.1分配再填充下的特征隔离

​  在此，我们旨在分离每个真实/伪造和先前/新领域的分布，并减轻覆盖以保留知识并积累从新任务和先前任务中学习到的伪造信息。

​  分配再填充(DR，Distribution Re-filling)
​  为了进一步促进不同分布的隔离，我们提出利用SUR稀疏均匀重放集的稀疏均匀性，在重放数据点和质心之间重新填充潜在空间分布。具体来说，由于SUR可以被看作是先前全局分布的均匀稀疏子集，因此SUR稀疏均匀重放特征与质心之间的空间也应属于相同的先前全局分布。因此，我们可以利用潜在空间混合来补充并进一步模拟之前的全局分布，从而增强特征隔离。所提出的分配再填充操作涉及来自同一重放集的两个随机特征（f₁和f₂）及其对应的质心(c)。该过程可表示为： \[\mathbf{f}_{\mathrm{filled}}=\beta(\alpha\mathbf{f}_{1}+(1-\alpha)\mathbf{f}_{2})+(1-\beta)\mathbf{c},\] ​  其中\(\alpha,\beta\ \in\ [0,1]\)为随机混合比例。通过这种方式，我们能够有效填充由顶点f₁、f₂和c构成的三角区域，从而在新任务训练时进一步促进特征隔离。通过这样做，我们可以有效地重新填充由顶点f1、f2和c形成的三角形区域，从而在新任务的训练中进一步促进特征隔离。

​  隔离损失
​  通过使用SUR稀疏均匀重放和再填充数据，我们可以引入监督对比损失[18]来区分真实/虚假和先前/新分布的每个特征域。具体而言，隔离损失可表示为： \[{\cal L}_{i s o}=-{\frac{1}{N}}\sum_{i=1}^{N}\log(\frac{\exp(\mathbf f_{i}\cdot\mathbf f_{j}/\tau)}{\sum_{k=1}^{N}{\mathbb{I}_{[y_{i}\neq y_{k}]}\exp({\mathbf f_{i}\cdot{\mathbf f_{k}/\tau}})}})\] ​  其中，\(\mathbf f_{i}\)和\(\mathbf f_{j}\)是来自同一领域的特征。\(y_i\)表示\(\mathbf f_{i}\)的领域标签，并为每个真实/虚假和先前/新领域分配一个唯一的值。\(\mathbb{I}_{[y_{i}\neq y_{k}]}\)表示一个指示函数，当\(y_i\)等于\(y_k\)时，该函数值为1；否则为0。值得注意的是，如果这些特征来自新的任务，则它们可能是当前训练数据的特征；如果这些特征来自先前的任务，则它们可能是由SUR或重填充数据生成的。同时，为了促进对不同真实领域的学习，来自不同任务的真实数据也被分配了不同的唯一yi值。
​  特征隔离机制通过阻止增量任务被先前任务覆盖，有效缓解了灾难性遗忘问题。同时，该机制促使骨干提取器能够区分各任务的不同领域，从而增强了其对各类伪造信息的敏感度。

3.4.2增量决策一致性

​  虽然特征隔离技术能有效降低特征覆盖效应并提升主干网络对伪造信息的敏感度，但如何直接从任务独立的特征域中提取最终的二值检测结果仍面临挑战。为此，我们提出增量决策对齐（Incremental Decision Alignment，简称IDA）方法，通过整合多类别独立特征中积累的伪造信息，为最终的二值检测结果提供有效支持。
​  IDA的目标是使所有任务中每个独立真实/虚假领域的决策边界保持一致。通过这种方式，我们既能促进特征隔离，又能优化统一的决策边界，从而在最终检测中有效区分真实与虚假领域。对于对齐任务，首先需要针对每个任务分别训练并获取真实/伪造的个体边界。因此，我们首先为同一任务中的真实样本和伪造样本分配并维护独立的分类器。这些分类器可视为每个任务的独立决策边界。第t个任务的分类器记作\({\cal C^{t}}(*;\theta^{t})\)，其中\(\theta^{t}\)是\({\cal C^{t}}\)的参数。为确保所有任务保持一致性，只需将递增的\({\cal C^{t+1}}(*;\theta^{t+1})\)与前一个\({\cal C^{t}}(*;\theta^{t})\)进行对齐即可，从而实现所有任务的递归对齐。由于区分真实/伪造的分类器属于线性层，对决策边界的对齐等同于确保线性参数的角度一致性。因此，针对\({\cal C^{t+1}}(*;\theta^{t+1})\)的决策对齐优化步骤可形式化表述为： \[\theta^{t+1}\leftarrow\left\|\theta^{t+1}\right\|_{2}\cdot\frac{(1-\gamma)\tilde{\theta}^{t+1}+\gamma\tilde{\theta}^{t}}{\left\|(1-\gamma)\tilde{\theta}^{t+1}+\gamma\tilde{\theta}^{t}\right\|_{2}},\] ​  其中\(\tilde{\theta} =\frac{\theta}{\|\theta\|_{2}}\)，γ表示学习率。在训练第（t+1）个任务时，分类器\({\cal C^{t+1}}\)会按照公式等式6进行优化以与\({\cal C^{t}}\)保持一致，而所有先前的分类器则被冻结，以维持原有的决策边界及其对齐状态。

3.5.训练和推理

​  训练
​  在训练第（t+1）个任务时，将把第1到第t个重放缓冲集与第（t+1）个训练数据合并为\({\bf X}=\{\hat{\bf X}^{1},\hat{\bf X}^{2},...,\hat{\bf X}^{t},{\bf X}^{t+1}\}\)。随后通过特征提取公式\(\mathbf{F}\ =\ {\cal{E}}^{t+1}(\mathbf{X})\)，可获得其特征向量\(\mathbf{F}=\{\hat{\mathbf{F}}^{1},{\hat{\mathbf{F}}}^{2},...,{\hat{\mathbf{F}}}^{t},\mathbf{F}^{t+1}\}\)。根据知识蒸馏损失函数的定义，我们还通过以下方式保留前序任务学习的信息： \[\mathcal{L}_{d i s}\Longrightarrow\sum_{i=1}^{t}(\hat{\bf F}^{i}-\mathcal{L}^{t}(\hat{\bf X}^{i}))^{2}\] ​  需要说明的是，\({\cal{E}}^{t}\)是基于前t次任务训练得到的冻结主干提取器。随后，我们通过引入带分配再填充的隔离损失函数（\({\cal L}_{iso}\)）来实现特征隔离。最终，二值检测损失函数可表示为： \[\mathcal{L}_{d e t}=\sum_{i=1}^{t}\mathrm{C}\mathrm{E}(\mathcal{C}^{i}(\hat{\mathrm{F}}^{i}),{\bf Y}^{i})+\mathrm{C}\mathrm{E}(\mathcal{C}^{t+1}(\mathrm{F}^{t+1}),{\bf Y}^{t+1}),\] ​  其中，CE表示交叉熵损失函数，\({\bf Y}^{t}\)是第t个任务的二元检测标签。因此，整体损失函数可表示为： \[\mathcal{L}_{\mathrm{overal}}=\mathcal{L}_{i s o}+\mu_{1}\mathcal{L}_{d i s}+\mu_{2}\mathcal{L}_{d e t},\] ​  其中μ₁和μ₂是权衡参数。在通过反向传播优化\(\mathcal{L}_{\mathrm{overal}}\)后，我们应用等式6来优化对齐的决策边界。

​  推理
​  在推理期间，输入图像x首先被\(\cal E\)处理为特征f。由于在实际应用的推理过程中，x的具体任务是未知的，因此我们无法确定具体的分类器用于推理。考虑到所有分类器都具有对齐的决策边界，我们采用它们的平均检测结果作为最终的推理结果，其表达式可表示为： \[y_{\mathrm{infer}}=\sum_{i=1}^{t+1}\frac{C^{i}({\bf f})}{t+1}.\]

4.实验结果

5.结论

​  在本文中，我们提出了一种新的对齐特征隔离技术，旨在提升增量面部伪造检测（Incremental Face Forgery Detection，IFFD）的性能。具体而言，我们将当前任务与之前任务的特征分布‘逐块’叠加，以减轻全局分布的覆盖效应，积累多样化的伪造信息，从而解决灾难性遗忘问题。随后，我们引入了一种新的稀疏均匀重播（Sparse Uniform Replay，SUR）策略和潜在空间增量检测器（Latentspace Incremental Detector，LID），以实现对齐特征隔离。通过在新的高级IFFD评估基准上的实验，我们显著证明了所提出方法的优越性。