K-means聚类

分类 - K-means聚类
How to Use K-means for Big Data Clustering?
How to Use K-means for Big Data Clustering?

发表于Pattern Recognition 2023， 设计了一个优化kmeans的算法BigMeans。

1
K-means聚类
PiCIE:Unsupervised Semantic Segmentation using Invariance and Equivariance in Clustering
PiCIE:Unsupervised Semantic Segmentation using Invariance and Equivariance in Clustering

发表于CVPR2021，无监督语义分割，使用聚类伪标签和交叉熵损失，同时使用数据增强，利用增强不变性，提高模型泛化性，是模型不关注噪声。（引用290次）

2
K-means聚类无监督语义分割
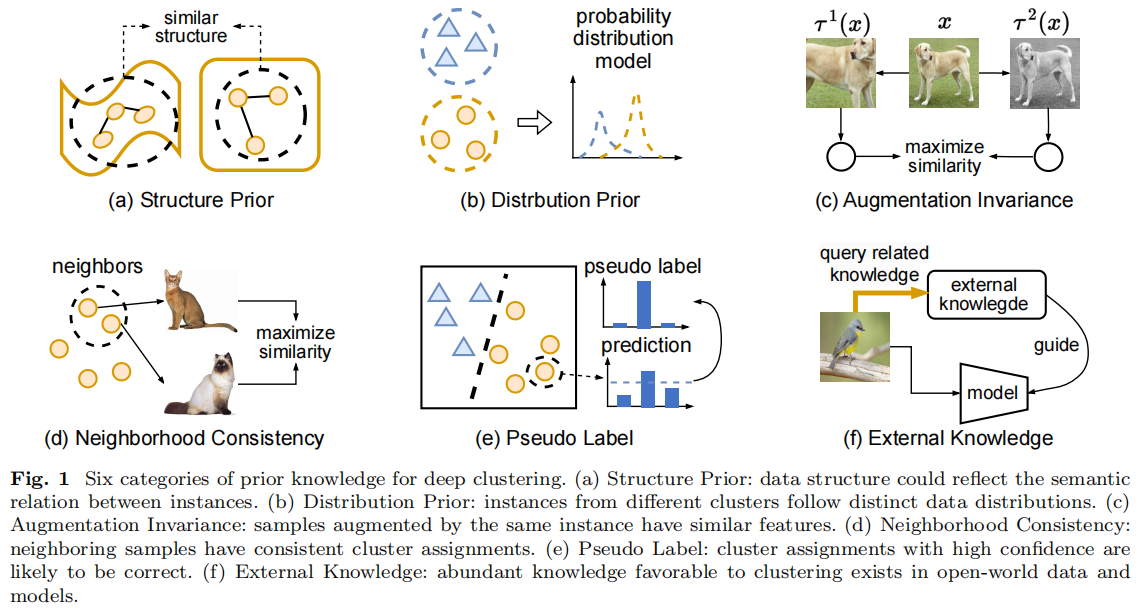
A Survey on Deep Clustering:From the Prior Perspective
A Survey on Deep Clustering:From the Prior Perspective

发表于Vicinagearth 2024，从先验的角度看深度聚类方法，(a)结构先验：数据结构可以反映实例之间的语义关系。(b)分布先验：来自不同集群的实例遵循不同的数据分布。(c)增强不变性：由相同实例增强的样本具有相似的特征。(d)邻域一致性：相邻的样本具有一致的聚类分配。(e)伪标签：具有高可信度的聚类分配很可能是正确的。(f)外部知识：在开放世界的数据和模型中存在大量有利于聚类的知识。

3
K-means聚类
Pixel and region level information fusion in membership regularized fuzzy clustering for image segmentation
Pixel and region level information fusion in membership regularized fuzzy clustering for image segmentation

发表于Information Fusion 2023。

4
K-means聚类
Deep Adaptive Fuzzy Clustering for Evolutionary Unsupervised Representation Learning
Deep Adaptive Fuzzy Clustering for Evolutionary Unsupervised Representation Learning

发表于IEEE Transactions on Neural Networks and Learning Systems 2023，提出了DAFC来自动分组图像，得到的迭代优化问题可以通过小批量RMSprop和反向传播而不是SGD有效地解决，可以学习一个更聚类友好的瓶颈空间。

5
K-means聚类
Robust deep fuzzy K-means clustering for image data
Robust deep fuzzy K-means clustering for image data

发表于JCR一区、CCF B类期刊的Pattern Recognition 2024，提出了一种新的边界引导图像篡改定位模型，该模型通过精心设计的注意力和对比学习机制充分利用被篡改区域的边界信息，利用拉普拉斯正则化方法对隶属度矩阵进行约束，使从相似样本中学习到的隶属度也相互关联，将自适应损失函数引入到统一的框架中，可以减少各种异常值的影响，有助于增强聚类的鲁棒性。

6
K-means聚类
Robust deep k-means:An effective and simple method for data clustering
Robust deep k-means:An effective and simple method for data clustering

发表于PR 2021。

7
K-means聚类
K-means clustering algorithms:A comprehensive review, variants analysis, and advances in the era of big data
K-means clustering algorithms:A comprehensive review, variants analysis, and advances in the era of big data

发表于Information Sciences 2023。

8
K-means聚类
Deep Clustering:A Comprehensive Survey
Deep Clustering:A Comprehensive Survey

发表于IEEE Transactions on Neural Networks and Learning Systems 2024，深度聚类的综合综述。

9
K-means聚类
avatar
Zhaozw
人完成了引以为豪的事,才能够感到荣耀，否则,虚伪的自豪只会腐蚀心灵。
文章
98
标签
18
分类
16
Follow Me
公告
可以用表情包和匿名评论了
分类
标签
合集 JS散度 边缘增强 报告 两阶段 双流（噪声图） BayarConv 多尺度 区域建议网络RPN UNet hrnet Query-Based SRM卷积 TruFor 扩散模型去噪预训练 Mask-Guided 比赛 讲座
归档
网站资讯
文章数目 :
98
本站访客数 :
本站总访问量 :
最后更新时间 :