来自维基百科，一个免费的百科全书

一、介绍

基于密度的噪声应用空间聚类（DBSCAN，Density-based spatial clustering of applications with noise）是由马丁·埃斯特、汉斯-彼得·克里格尔、桑德和徐小伟于1996年提出的一种数据聚类算法。[1]这是一种基于密度的聚类非参数算法：给定某些空间中的一组点，它将紧密排列的点（有许多相邻的点）聚在一起，并标记为低密度区域的异常点（那些最近的邻居太远）的异常点。DBSCAN是最常用和最被引用的聚类算法之一。[2]
2014年，在领先的数据挖掘会议ACM SIGKDD上，该算法获得了时间测试奖（授予在理论和实践上受到大量关注的算法）。[3]截至2020年7月，后续论文“DBSCAN重访，重访：为什么你应该和如何（仍然）使用DBSCAN”[4]出现在著名的ACM数据库系统交易（TODS）期刊的8篇下载次数最多的文章列表中。
另一个后续文章HDBSCAN*最初由Ricardo J. G. Campello, David Moulavi和Jörg Sander于2013年出版，[6]在2015年与亚瑟·齐梅克进行了扩展。[7]它修改了一些原始的决策，如边界点，并产生了一个层次化的结果，而不是一个平坦的结果。

二、历史

1972年，Robert F. Ling在计算机期刊上的“k-簇的理论和构建”[8]中发表了一个密切相关的算法，估计运行时复杂度为O（n³）。[8] DBSCAN的最坏情况是O（n²），而面向数据库的DBSCAN的范围查询公式允许索引加速。这些算法在处理边界点上略有不同。

三、准备工作

考虑某个空间中的一组点。设ε是一个参数，指定一个邻域相对于某个点的半径。为了进行DBSCAN聚类，将这些点划分为核心点、（直接-）可达点和异常值，如下：

如果至少有minPts点在它的距离ε范围内（包括p），则点p是一个核心点。
如果点q与核心点p在距离ε内，则点q可以直接从p到达。点只说可以从核心点直接到达。
如果有一个路径p1，...，pn，且p1 = p和pn = q，则一个点q可以从p到达，其中每个pi+1可以直接从pi到达。注意，这意味着初始点和路径上的所有点必须是核心点，可能的q除外。
所有不能从任何其他点可到达的点都是异常值或噪声点。

现在，如果p是一个核心点，那么它与从它可以到达的所有点（核心或非核心）一起形成一个集群。每个集群中至少包含一个核心点；非核心点可以是集群的一部分，但它们形成了集群的“边缘”，因为它们不能被用来到达更多的点。

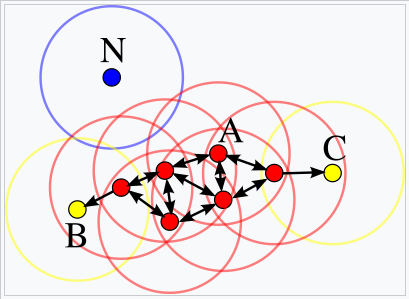
在这个图中，minPts = 4。点A和其他红点是核心点，因为在ε半径内，这些点周围的区域中包含了至少4个点（包括点本身）。因为它们都是相互访问的，所以它们形成了一个单独的集群。点B和点C不是核心点，但可以从A到达（通过其他核心点），因此也属于集群。N点是一个既不是核心点，也不是直接可到达的噪声点。
可达性不是一种对称的关系：根据定义，只有核心点才能到达非核心点。相反的，所以一个非核心点可能可以到达，但什么也不能到达。因此，需要进一步的连通性概念来正式定义DBSCAN发现的集群的范围。两点p和q是密度连接的，如果有一个点o使得p和q都是从o可到达的。密度-连通性是对称的。
然后一个集群满足两个属性：

簇内的所有点都是相互密度连接的。
2. 如果一个点是从集群的某个点可以到达密度的，那么它也是集群的一部分。

四、算法

1.原始基于查询的算法

DBSCAN需要两个参数： ε（eps）和形成密集区域[a]（minPts）所需的最小点数。它从一个未被访问过的任意起点开始。检索这个点的ε邻域，如果它包含足够多的点，就启动一个集群。否则，该点将被标记为噪声。请注意，这个点以后可能会在另一个不同点的足够大小的ε环境中找到，因此会成为集群的一部分。
如果一个点被发现是一个集群的密集部分，它的ε邻域也是该集群的一部分。因此，在ε邻域内发现的所有点都被添加起来，当它们自己的ε邻域也很密集时。这个过程一直持续到密度连接的集群完全找到。然后，一个新的未访问的点被检索和处理，导致发现进一步的集群或噪声。
DBSCAN可以用于任何距离函数[1] [4]（以及相似度函数或其他谓词）。[9]因此，距离函数（dist）可以看作是一个附加的参数。该算法可以用伪代码表示如下：[4]

DBSCAN(DB, distFunc, eps, minPts) {
    C := 0                                                  /* 集群计数器 */
    for each point P in database DB {
        if label(P) ≠ undefined then continue               /* 在内循环中预处理 */
        Neighbors N := RangeQuery(DB, distFunc, P, eps)     /* 找领域 */
        if |N| < minPts then {                              /* 密度检查 */
            label(P) := Noise                               /* 标记为噪音 */
            continue
        }
        C := C + 1                                          /* 标记为下一个聚类 */
        label(P) := C                                       /* 标记为原点 */
        SeedSet S := N \ {P}                                /* 要扩展的邻域 */
        for each point Q in S {                             /* 处理每个种子点Q */
            if label(Q) = Noise then label(Q) := C          /* 将噪声更改为边界点 */
            if label(Q) ≠ undefined then continue           /* 预处理 (e.g., 边界点) */
            label(Q) := C                                   /* 标记为邻域 */
            Neighbors N := RangeQuery(DB, distFunc, Q, eps) /* 找领域 */
            if |N| ≥ minPts then {                          /* 密度检查 (如果Q是一个核心点) */
                S := S ∪ N                                  /* 向种子集添加新的邻域 */
            }
        }
    }
}

其中RangeQuery可以使用数据库索引来实现更好的性能，或使用缓慢的线性扫描：

RangeQuery(DB, distFunc, Q, eps) {
    Neighbors N := empty list
    for each point P in database DB {                      /* 扫描数据库中的所有点 */
        if distFunc(Q, P) ≤ eps then {                     /* 计算距离并检查距离 */
            N := N ∪ {P}                                   /* 添加到结果 */
        }
    }
    return N
}

2.抽象算法

DBSCAN算法可以抽象为以下步骤：[4]

找到每个点的ε（eps）邻域中的点，并识别出超过minPts邻域的核心点。
在邻居图上找到核心点的连通分量，忽略所有的非核心点。
如果集群是一个ε（eps）邻居，则将每个非核心点分配给附近的集群，否则将其分配给噪声。

一个简单的实现需要在步骤1中存储社区，因此需要大量的内存。最初的DBSCAN算法不需要一次执行一个点执行这些步骤。

3.优化标准

DBSCAN优化以下损失功能：[10]对于任何可能的集群\(C=\{C_{1},\ldots,C_{l}\}\)的所有的集群\(\cal{C}\)，它减少集群的数量条件下，每一对点集群是密度可达的，这对应于最初的两个属性“最大性”和“连接”的集群：[1] \[{\displaystyle \min _{C\subset {\mathcal {C}},~d_{db}(p,q)\leq \varepsilon ~\forall p,q\in C_{i}~\forall C_{i}\in C}|C|}\] 其中\({\displaystyle d_{db}(p,q)}\)给出最小的\(\varepsilon\)，这样两点p和q是密度连接的。

4.复杂度

DBSCAN访问数据库的每个点，可能会访问多次（例如，作为不同集群的候选点）。然而，出于实际考虑，时间复杂度主要由区域查询调用的数量决定。DBSCAN执行一个这样的查询，如果使用一个索引结构，执行一个邻居查询O(n log n)，一个整体平均运行时复杂度的O(n log n)（如果参数ε选择在一个有意义的方式，例如，平均只有O(n log n)点返回）。如果不使用加速索引结构，或对退化数据（例如，在距离小于ε范围内的所有点），最坏情况下的运行时复杂度仍然是O（n²）。距离矩阵的上三角形\({\displaystyle \textstyle {\binom {n}{2}}} - n = (n²-n)/2\)可以物化以避免距离重新计算，但这需要O（n²）内存，而基于非矩阵的DBSCAN实现只需要O (n)内存。

5.优势

DBSCAN不需要预先指定数据中的集群数量，而不是k-means。
2. DBSCAN可以找到任意形状的团簇。它甚至可以找到一个完全被一个不同的集群包围（但没有连接到）的集群。由于MinPts参数，所谓的单链效应（不同的簇通过一条细点线连接）被减少。
3. DBSCAN有噪声的概念，并且对异常值具有鲁棒性。
4. DBSCAN只需要两个参数，并且对数据库中的点的排序大多不敏感。（然而，如果点的顺序发生了改变，那么位于两个不同集群边缘的点可能会交换集群成员关系，并且集群分配仅在同构之前是唯一的。）
5. DBSCAN是为使用可以加速区域查询的数据库而设计的，例如使用R*树。
6. 如果数据理解，minPts可以由领域专家设置参数mints和ε。

6.劣势

DBSCAN并不是完全确定性的：可以从多个集群中可访问的边界点可以是任何一个集群的一部分，这取决于数据被处理的顺序。对于大多数数据集和域，这种情况并不经常出现，对聚类结果的影响也很小：[4]无论是核心点还是噪声点，DBSCAN都是确定性的。DBSCAN*[6] [7]是一种将边界点视为噪声的变化，这种方式实现了完全确定的结果以及密度连接分量的更一致的统计解释。
2. DBSCAN的质量取决于函数区域查询（P，ε）中使用的距离度量。最常用的距离度量是欧氏距离。特别是对于高维数据，由于所谓的“维数诅咒”，这个度量几乎变得无用，使得很难为ε找到合适的值。然而，这种效应也存在于任何其他基于欧氏距离的算法中。
3. DBSCAN不能很好地聚类密度差异很大的数据集，因为不能适当地选择minPts-ε组合。[11]
4. 如果数据和规模没有被很好地理解，那么选择一个有意义的距离阈值ε可能是困难的。

请参阅下面的扩展部分，以了解处理这些问题的算法修改。

7.参数估计

每个数据挖掘任务都存在参数问题。每个参数都会以特定的方式影响算法。对于DBSCAN，需要参数ε和minpt。这些参数必须由用户指定。理想情况下，ε的值是由要解决的问题（例如物理距离）给出的，然后minPts是期望的最小簇大小。[a]

MinPts：根据经验，最小的MinPts可以从数据集中的维数D中得到，如MinPts≥D + 1。minPts = 1的低值没有意义，因为每个点都是一个核心点。使用minPts≤2，结果将与单链接度量的层次聚类相同，树状图切割高度为ε。因此，minPts 必须选择至少为3。然而，对于有噪声的数据集，更大的值通常更好，并将产生更显著的集群。根据经验法则，可以使用minPts=2·dim，[9]，但对于非常大的数据、有噪声的数据或包含许多重复的数据，可能需要选择更大的值。[4]
ε：ε的值可以用一个k-distance graph来选择，绘制到 k = minPts-1 个最近邻的距离，按从最大值到最小值的顺序排列。[4]ε的良好值是这个图中显示一个“肘部”的地方：[1] [9] [4]如果选择ε太小，大部分数据将不会聚集；而如果ε值过高，集群将合并，大多数对象将在同一个集群中。一般来说，小的ε值更可取，[4]和作为经验法则，只有一小部分点应该在这个距离内彼此。或者，一个 OPTICS 图可以用来选择ε，[4]，但然后OPTICS算法本身也可以用来聚类数据。
距离函数：距离函数的选择与ε的选择紧密耦合，对结果有重大影响。一般来说，在选择参数ε之前，需要首先为数据集确定一个合理的相似性度量。对这个参数没有估计，但需要为数据集适当地选择距离函数。例如，在地理数据上， great-circle distance 通常是一个很好的选择。

OPTICS 可以看作是DBSCAN的泛化，它用最影响性能的最大值代替ε参数。然后，MinPts基本上成为了要找到的最小集群大小。虽然该算法比DBSCAN更容易参数化，但结果使用起来有点困难，因为它通常会产生分层聚类，而不是DBSCAN产生的简单数据分区。
最近，DBSCAN的一位原始作者重新回顾了DBSCAN和OPTICS，并发表了一个改进版本的分层DBSCAN（hdbscan*），[6] [7]，它不再有边界点的概念。相反，只有核心点构成了集群。

8.与光谱聚类的关系

DBSCAN的光谱实现与在确定连通图组件的平凡情况下的光谱聚类有关——没有边切割的最优聚类。[12]然而，它可以是计算密集型的，高达 \(\displaystyle O(n^{3})\) 。此外，还必须选择特征向量的数量来计算。由于性能原因，原始的DBSCAN算法仍然优于其光谱实现。

9.延伸

广义DBSCAN（GDBSCAN）[9] [13]是由同一作者对任意“邻域”和“密集”谓词的推广。ε和minPts参数将从原始算法中删除，并移动到断言中。例如，在多边形数据上，“邻域”可以是任何相交的多边形，而密度谓词使用多边形区域，而不仅仅是对象计数。对DBSCAN算法提出了各种扩展，包括并行化方法、参数估计和对不确定数据的支持。利用光学算法将其基本思想扩展到层次聚类中。DBSCAN也被用作子空间聚类算法的一部分，如PreDeCon和SUBCLU。HDBSCAN*[6] [7]是DBSCAN的一个层次版本，它也比光学更快，它可以从层次中提取一个由最突出的集群组成的平面分区。[14]

五、源自

DBSCAN - Wikipedia