Deep Adaptive Fuzzy Clustering for Evolutionary Unsupervised Representation Learning
Deep Adaptive Fuzzy Clustering for Evolutionary Unsupervised Representation Learning
摘要
在模式识别和计算机视觉中,大型和复杂数据集的聚类分配是一项关键但具有挑战性的任务。在本研究中,我们探索了在深度神经网络框架中使用模糊聚类的可能性。因此,我们提出了一种新的具有迭代优化的进化无监督学习表示模型。它实现了深度自适应模糊聚类(DAFC)策略,从只给定的未标记数据样本中学习卷积神经网络分类器。DAFC由深度特征质量验证模型和模糊聚类模型组成,其中实现了深度特征表示学习损失函数和具有加权自适应熵的嵌入式模糊聚类。我们将模糊聚类联合到深度重建模型中,其中利用模糊隶属度来表示一个清晰的深度聚类分配结构,并联合优化深度表示学习和聚类。同时,该联合模型通过检查从估计的瓶颈空间重采样的数据是否具有一致的聚类特性来评估当前的聚类性能,从而逐步改进深度聚类模型。在不同数据集上的实验表明,与其他先进的深度聚类方法相比,该方法在重建和聚类质量方面都有更好的性能,大量实验的深入分析证明了这一点。
I.介绍
受深度特征学习框架、深度信念网络(DBN)[18]和稀疏自编码器层次结构[19]、[20]的成功启发,它们试图从输入数据中提取特征,如反进化网络,贪婪地以无监督的方式从图像向上构建层。在这些研究中,每一层都由具有聚类模型的编码器和解码器组成。此外,用于深度聚类的卷积神经网络(CNN)架构,其中变分自编码器(VAE)是用于深度生成学习的非常强大的无监督框架。在深度聚类中广泛使用的cnn是堆叠自动编码器(SAEs)[21]和结构化自动编码器(StructAE),它们结合了基于图的聚类来实现精确的深度表示。它们都采用了多阶段管道,用无监督学习方法对统一的深度网络模型进行预训练,并对大规模图像实现了传统的聚类方法作为后处理。然而,它们在聚类分配中进行深度聚类,且高度依赖于预先训练好的相似度矩阵,因此在大数据集上的聚类性能不够好。
此外,Yang等人的[11]使用循环框架迭代地学习深度特征表示和聚类分配。该框架在聚类模型中的连续操作被表示为循环过程中的步骤,并堆叠在通过cnn输出的表示方式之上。他们的模型在小的复杂数据集上表现出了很好的性能,但可能对多凸网竞争所需的大量复杂图像具有挑战性。深度嵌入式聚类(DEC)[22]是一种著名的深度网络结构,它可以同时实现特征表示和聚类模型来训练复杂的数据集。该方法通过采用高度机密的样本作为监督,使每个聚类中样本的分布更密集、更清晰地分组。然而,在使用随机梯度下降(SGD)训练大而复杂的数据集时,并不能保证将样本拉到正确的聚类附近,这也不能保证快速收敛。
虽然卷积网方法的联合聚类和特征学习在无监督学习中表现出了显著的性能,但在特征聚类和网络参数更新之间交替的训练计划导致特征表示[23]的学习不稳定。此外,它们也没有联合优化深度表示学习和聚类。具有自进化聚类[24]和大规模多目标决策聚类[25]的深度对流模型由于能够处理大规模数据集和复杂的表示而受到越来越多的关注。由于计算复杂度高,深度卷网络结构的应用通常需要一个具有强大计算能力的平台。一些聚类方法已经用深度共流网络进行了研究,但深度聚类的关键成分仍不清楚。例如,如何有效地将实例为巨大的复杂数据分组到集群中,并提供定义面向集群的损失函数的有效信息?如何在精度和效率之间实现良好的权衡,并提高深度卷网的聚类性能?哪些类型的神经网络结构适合用于聚类的特征表示学习?
在本研究中,我们的目标是开发新的进化表示学习解决方案的深度无监督聚类问题。综上所述,本研究的主要贡献如下。
- 我们提出了DAFC来自动分组图像,得到的迭代优化问题可以通过小批量RMSprop和反向传播而不是SGD有效地解决,可以学习一个更聚类友好的瓶颈空间。
2. 我们仔细地制定了一个目标,以包含对高聚类性能至关重要的三个关键方面:有效的潜在表示空间、相似度度量和深度聚类的加权自适应熵,它们可以集成到深度学习架构中
3. 与单独优化这些目标的情况相比,这种深度进化无监督表示学习对网络损失和具有模糊聚类的重建损失提供了优越的性能。
4. 加权自适应熵的深度聚类,我们计算模糊会员和最优权重作为全局变量,可以共同优化深度表示学习,有效地组实例到集群为巨大的复杂数据和实现一个好的权衡精度和效率,以及进一步提高深度双convnet集群的性能。
本研究的其余部分组织如下。我们首先回顾了在第二节中包含一些有效的深度聚类框架的相关工作。我们在第三节提出的深度自适应模糊聚类(DAFC)。在第四节中,我们讨论了最先进的深度聚类方法的结果和分布,并将它们与我们的方法进行了比较。本研究的结论和今后的工作见第五节。
II.相关工作
VAE的网络由编码器和解码器组成,其中潜在特征层后面是潜在特征层,如图1所示。
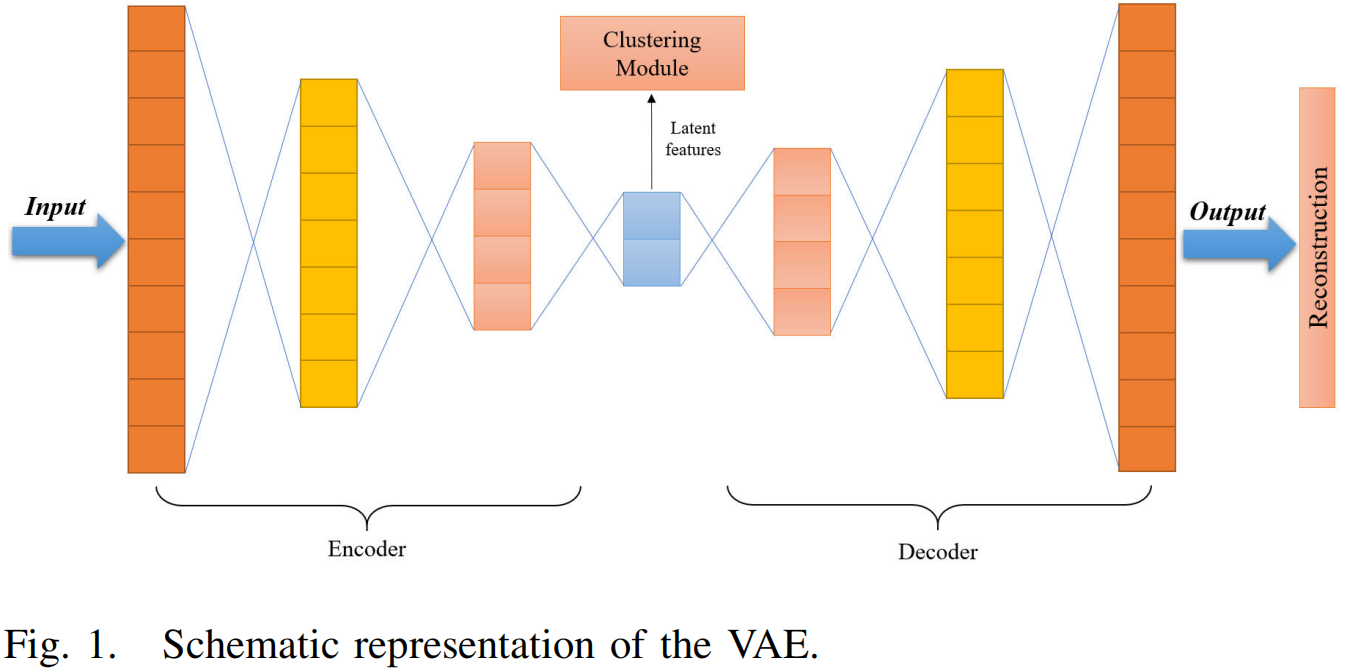
编码器将输入的样本映射到潜在的特征层。潜在特征层从编码器模型中学习输入数据的潜在特征,并将高维特征映射到低维子空间,然后利用聚类模型对所映射的数据进行划分。VAE的解码器恢复并重建特征,使特征数据能够重构为原始数据。期望VAE的输入和输出可以以一致的或无损的方式进行重构,且潜在特征向量的维数远小于输入样本的维数。使用学习到的潜在层来聚类分配和其他任务将更有效。该方法有利于学习更多重要的特征,而忽略了一些冗余的特征。但是,如果目标的大小与训练图像的背景有较大的差异,训练网络很容易忽略学习过程[34]中忽略目标特征。因此,当训练诸如ImageNet数据集等庞大而复杂的数据集时,VAE的精度并不高,甚至不能对其进行分区。
虽然该方案利用SAE和VAE将输入数据映射到一个具有代表性的特征空间,然后进行聚类分析,但特征表示空间和聚类方法是两个独立的过程,其目标函数没有联合优化。在第三节中,我们将基于ConvNets结构建立更深层次的EF和重建模型,并结合模糊聚类模型。
III.方法
在本节中,我们将描述我们的深度进化无监督表示学习,并表明通过深度聚类框架可以获得有用的通用的巨大和复杂的特征。
A.网络架构
基于统计学习和深度cnn的现代深度网络计算机视觉方法需要良好的图像特征化。在DAFC方法中,我们建立了一个更深入的FE模型和Rec模型,并通过潜在的表示瓶颈层将它们连接起来。瓶颈空间的有效潜在表示是深度进化无监督表示学习的一个关键方面,它可以更好地提取网络的每一层之间的特征。在联合聚类的瓶颈空间中构建了一个局部结构,以实现更好的聚类分配。与最先进的深度聚类相比,我们很容易假设这种优势是由于瓶颈空间可以通过最小化重构和聚类损失来保留输入数据的局部结构。我们设计了一种有效的基于凸面的模糊聚类模型分类器,以广泛地利用瓶颈空间,其中损失函数是重构损失和模糊聚类损失的和。
DAFC的网络体系结构的目标是将多层数据点划分为完全没有任何标签的集群,并联合优化深度表示学习,进一步提高了对异常值的鲁棒性。对于同一样本,不同类型的层(深和浅)之间的相互信息应该最大化。为了提高深度聚类的准确性,我们增加了模型中网络的特征训练层的数量。受ResNet
[35]和DenseNet学习[36]的启发,我们试图控制网络优化器,以便对SGD、Adam和RMSprop进行比较。在网络的梯度下降问题上,我们采用了一个较慢的学习速率来处理脊间的跳跃问题,这有助于获得更好的聚类性能。
所提出的网络模块的关键因素是,在我们的深度ConvNets模型中,我们使用了具有步幅的卷积层和池化层,而不是接在池化层后的卷积层。它不同于VAE的模块。在这项工作中设计的模块导致了更高的转换能力。我们对卷积层、ReLU层、批归一化、池化和退出层进行多个组合,如图2所示。
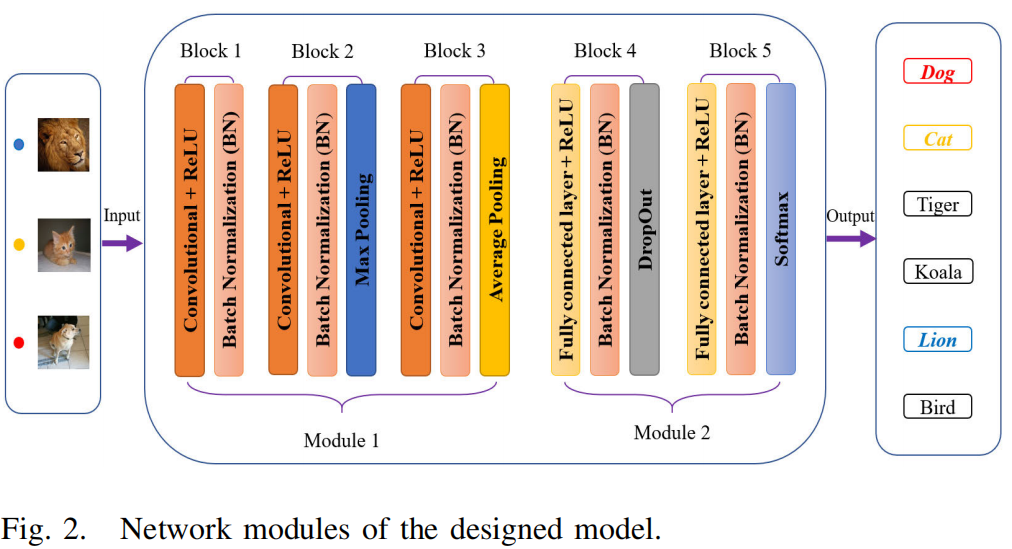
此外,深度ConvNets模型通常通过池层缩小特征映射的大小。所设计模型的每个模块通过前馈方式将每一层连接到每一层,模块1为22层前馈神经网络,具有前2层,模块2为8层。该模型采用多个全连通层作为瓶颈空间的潜在表示。我们还可以根据输入数据的要求,灵活地深化网络模块的建设。当在足够复杂的数据上进行训练时,该方法在标准的竞争分类基准上不断取得最佳性能。
在我们的网络模型中,我们使用多个全连接层,加深全连接层的数量,以提高模型的非线性表达式和特征学习能力。为了防止深化模型的学习能力过好,导致过拟合,我们添加了dropout层,然后是全连接层。dropout层只允许为每个反向传播调整部分网络参数。如图3所示,我们根据网络模块建立了DAFC的深度卷积神经网络模型。
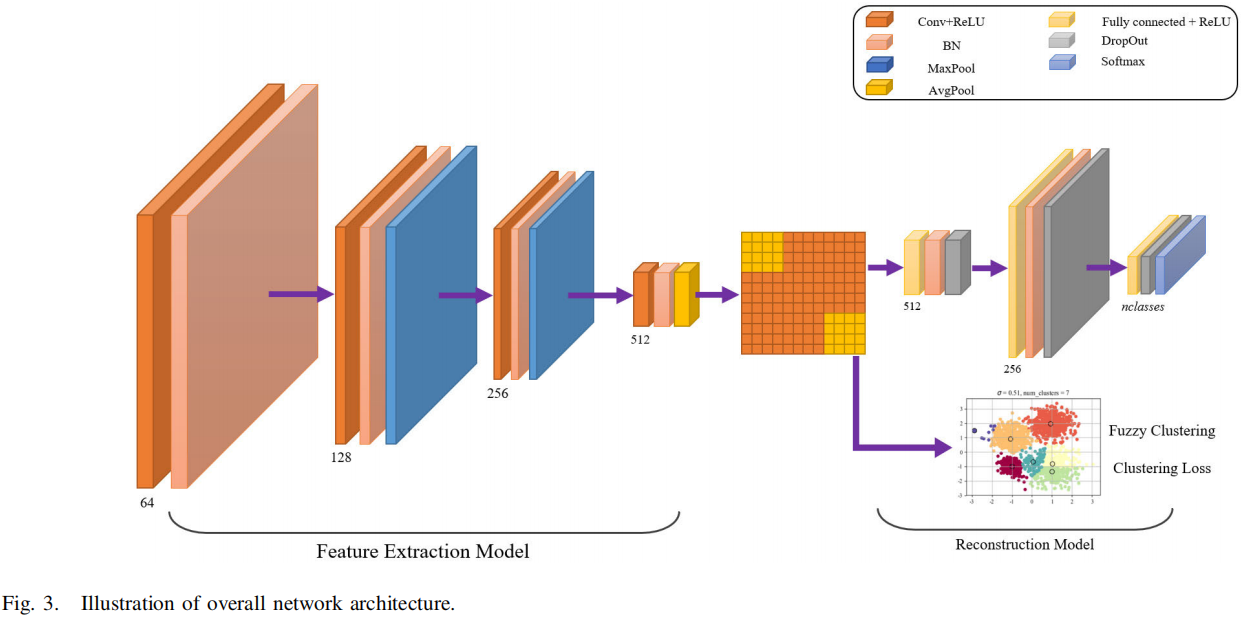
在这些模块中,每个块都有不同的功能层。此外,模块1和模块2分别对应于所设计的网络模型的每个部分。
在该网络体系结构中,模块1被设计为FE模型,模块2被设计为重构模型,如图2所示。FE模型提供了一个从输入到潜在表示瓶颈空间的自底向上的映射,而重构(Rec)模型将提取的特征映射回输入空间,希望能给出一个接近原始数据的重构。FE和重构模型,并通过卷积操作的潜在表示瓶颈层将它们连接起来。在联合模糊聚类的瓶颈空间中构建了一个局部结构,以实现更好的聚类分配。在Rec模型中,我们设计了一种有效的基于深度凸网的分类器,具有加权自适应熵模糊聚类模型,以广泛利用瓶颈空间。此外,我们还研究了一种联合策略,其中损失函数是最小化重建损失和模糊聚类损失的和,其中FE模型\(F = f_w (x)\)和Rec模型\(G\equiv
g_{\theta}(F)\)的参数。
为此,我们将FE模型的重构损失和模糊聚类损失同时结合为目标函数。深度卷积网络的FE模型保留了复杂数据生成分布的局部结构,避免了特征空间的破坏。然后,随着学习的进行,设计的深度卷积网络可以通过迭代训练来测量更准确的相似性,并且会逐渐选择更多的聚类任务来找到更精细的组。模糊聚类模型的目的是在大量和不同的数据点之间对相似或相同的模式进行分组。在这个深度聚类模型中,我们使用隶属度使聚类结果更具区分性,µ是数据点x属于第j个聚类的分配概率。
B.深度聚类策略
在我们的网络体系结构中,FE和Rec模型重叠了复杂多层次的所有特征,其中重叠的域,这是整个体系结构的层次组成。通过将l层的特征映射f (x)作为层l + 1的输入,可以很容易地堆叠形成层次,其中输入数据x到瓶颈空间Z (x)的初始非线性映射,如图4所示。
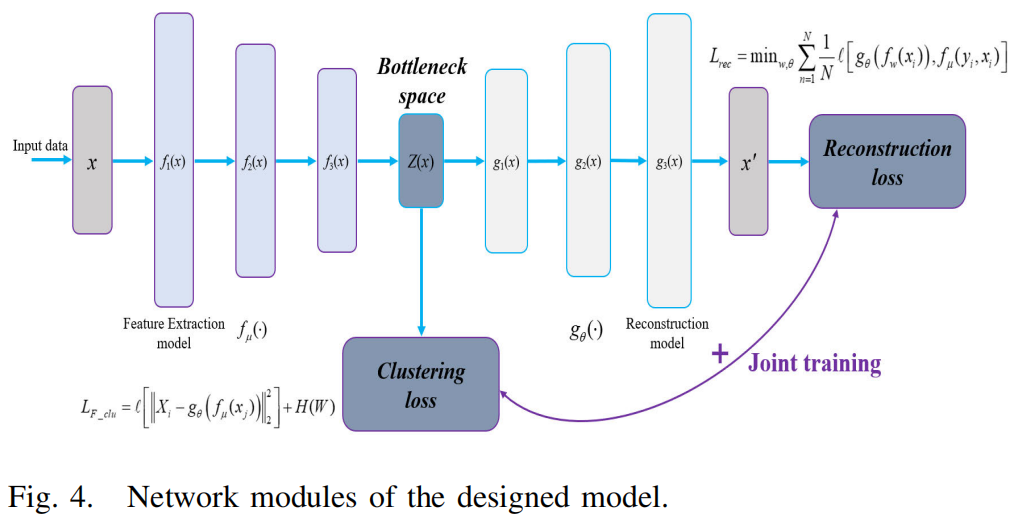
映射F和G通过FE模型和Rec模型实现,它们通过优化的瓶颈空间与卷积层和多个全连接层进行连接。改进了瓶颈空间表示,使具有属于同一集群的高概率的映射点对将被拉得更近在一起。因此,设计瓶颈空间将FE模型和Rec模型连接起来,这对联合模糊聚类更有意义。
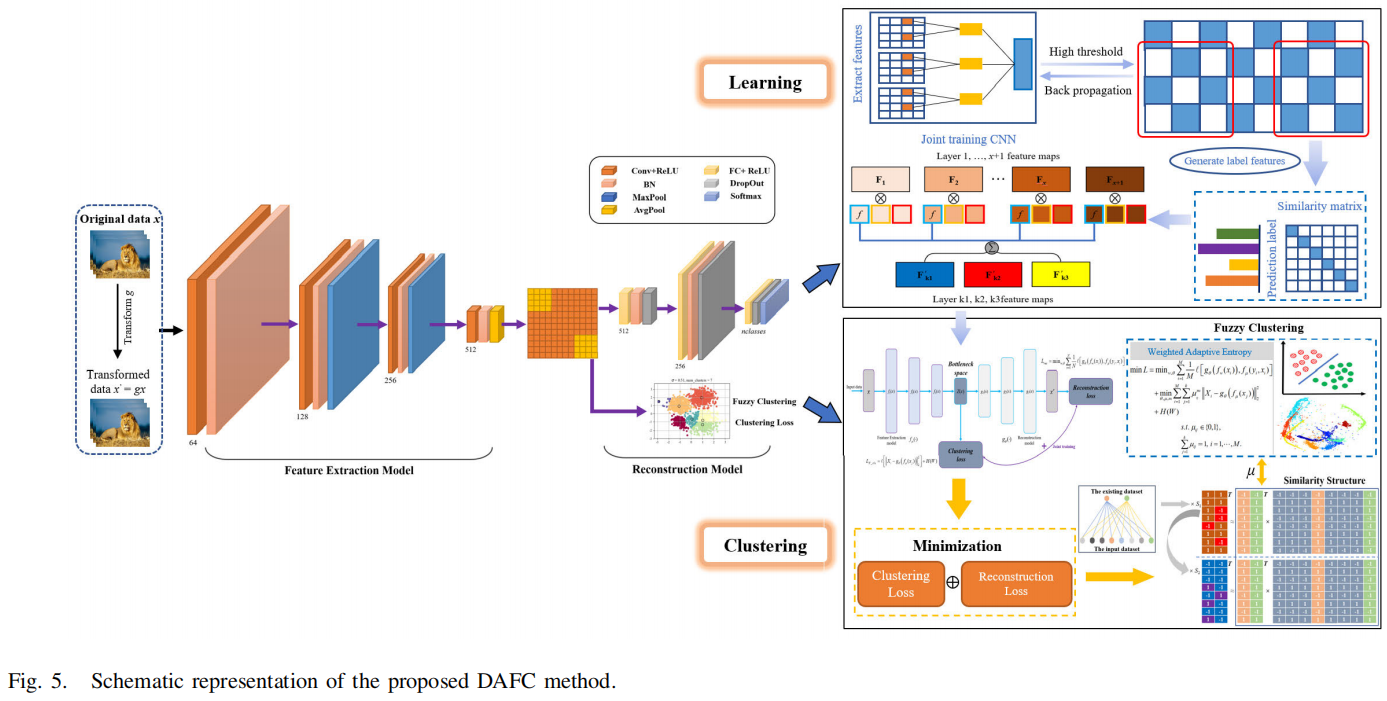
f是训练过程中模糊隶属度为\(\mu\)的瓶颈空间中输入数据的特征,如图5中的相似性结构所示,z为瓶颈空间表示。它们也代表了在网络超参数下由卷积网分类器进行的特征划分的结果。通过优化重构的损失函数,共同学习ConvNets分类器的参数θ和映射的参数w,公式如下:
\[{L}_{\mathrm{Rec}}=\operatorname*{min}_{w,\theta}\sum_{i=1}^{M}\frac{1}{M}\ell\left[g_{\theta}\left(f_{w}\left(x_{i}\right)\right),z_{i}\right]\]
首先,我们通过数据增强得到一批原始数据\(\{x\}\)加上转换后的数据\(\{x^{\prime}\}\),然后得到输入数据:\(x_i = x + x^{\prime}\)。\(x_i\)表示第i张图像,M为图像数。在输入数据中,每个图像\(x_i\)都与\(\{0,1\}^k\)中的一个标签\(y_i\)相关联。该网络将输入数据映射到紧凑的特征映射\(F=f_w(x_i)\)中,并对FE模型的输出进行聚类,然后使用后续的聚类分配作为伪标签来优化(1),并作为反馈信息反向传播到Rec模型中。下一步通过使用Rec模型的网络生成输入数据的特征标签,其中相似度矩阵从ConvNets的样本内存中读取该批数据的伪标签。图5是所提出的使用模糊聚类模型的深度进化无监督表示学习的示意图。我们在定义1中定义了相似矩阵,并对于潜在瓶颈空间表示\(z_{i}=f_{\mu}(y_{i},x_{i})\)。利用相似度矩阵,利用最优优化器对深度网络进行更新,结合模糊聚类模型如下:
\[{L}_{\mathrm{Rec}}=\operatorname*{min}_{w,\theta}\sum_{i=1}^{M}\frac{1}{M}\ell\left[g_{\theta}\left(f_{w}\left(x_{i}\right)\right),f_{\mu}\left(y_{i},x_{i}\right)\right]\] 其中\(f_{\mu}(\cdot)\)为相似度矩阵每一列设置的模糊隶属度,这种表示应该更准确。基于(2),我们进一步得到 \[f_{\mu}\left(y_{i},x_{i}\right)=C_{i,j}\left(x_{i}\right)\cdot y_{i}\]
定义1:相似矩阵。
我们假设C是生成特征标签的邻接矩阵,\(a_i\)是C的第i列。标签的节点i与节点j的相似性为
\[C_{i,j}(\cdot)=\frac{a_{i}^{T}a_{j}}{\|a_{i}\|}\
=\frac{a_{i}^{T}a_{j}}{\sqrt{d_{i}}\sqrt{d_{j}}}\]
我们将FE模型训练的特征转移到瓶颈空间,在目标中加入模糊聚类,并随着聚类损失进行优化。将模糊聚类模型的输出结果作为伪标签反向传播到ConvNets中,并对\(L_{Rec}\)进行优化,并对网络参数进行优化。在经过逐层贪婪训练后,通过反向传输将FE模型和Rec模型的所有层连接起来,构建深度联合训练模型。然后对联合模型进行微调,设置一个高阈值和两个权衡参数,以最小化重构信息的损失。Rec模型保留了伪标签生成分布的局部结构,避免了瓶颈空间的破坏。该深度聚类模型可以迭代地学习输入数据的特征,并对其进行划分。
此外,我们计算特征之间的相似性,并选择高置信度的生成的标签特征,通过联合框架反馈FE和Rec模型的训练。在Rec模型中,我们设置了一个高阈值来确定是否应该将一些图像伪标签合并到特征映射中。如果两个标签之间的相似性大于高阈值,并且我们将这种类型的标签分组属于同一个聚类。反馈的反向传播FE和Rec旨在学习基于卷积神经网络的深度映射函数g,该函数由θ参数化。通过模糊聚类模型最小化Rec的损失函数来更新联合框架的参数
\[L_{F_{-}\mathrm{clu}}=\ell\
[||X_{i}-g_{\theta}(f_{\mu}(x_{j}))||_{2}^{2}]+H(W)\\=
\operatorname*{min}_{\theta,\mu,m}\sum_{i=1}^{M}\sum_{j=1}^{k}\mu_{i
j}^{m}\left\|X_{i}-g_{\theta}\bigl(f_{\mu}\bigl(x_{j}\bigr)\bigr)\right\|_{2}^{2}+H(W)\]
式中,M为数据集中的数据样本数,j为第j个簇,k为簇分配的数量。
在模糊聚类的损失函数中,我们考虑了一个庞大而复杂的数据集的权值在瓶颈空间中被划分为聚类,它也代表了该数据特征映射在形成聚类中的贡献概率。我们进一步改进了加权自适应损失函数的模糊聚类,增加加权熵,刺激更多的特征有助于聚类识别。这样,DAFC模型即使使用加权自适应熵,也可以直接进行深度端到端训练,这种学习到的层次表示被证明对深度聚类任务是有效的。
定义2:深度聚类的加权自适应熵[44]。
假设聚类的权值信息为H (w),并同时设置最优模糊隶属度和\(w_{i j}\)的最优权值。H (w)的计算方法如下:
\[H(w)=\lambda_{1}\Biggl(1-\sum_{j=1}^{k}\mu_{i
j}\Biggr)+\lambda_{2}\sum_{i=1}^{M}\sum_{j=1}^{k}w_{i j}\log w_{i
j}\] 其中,\(\lambda_{1}\)是一个权衡参数,控制分配给各种类型异常值的模糊鲁棒性,\(\lambda_{2}\)也是一个权衡参数,控制模糊隶属度的簇分布。DAFC的目标函数是
\[\mathrm{min}\, L=L_{\mathrm{Rec}}+
L_{F_{-}\mathrm{clu}}\] 可改写如下: \[\begin{array}{ll}\operatorname*{min}L&=&\operatorname*{min}_{w,\theta}\sum_{i=1}^{M}\frac{1}{M}\cdot\ell\left[g_{\theta}\left(f_{w}\left(x_{i}\right)\right),f_{\mu}\left(y_{i},x_{i}\right)\right]\\&&+\operatorname*{min}_{\theta,\mu,m}\sum_{i=1}^{M}\sum_{j=1}^{k}\mu_{i
j}^{m}\cdot\ell\,\left\|X_{i}\,-\,g_{\theta}\big(f_{\mu}\big(x_{j}\big)\big)\right\|^{2}\\&&+H(W)\\&{\mathrm{s.t.}}&~\mu_{i
j}\in\{0,1\}\\&&\sum_{j=1}^{k}\mu_{i j}=1,\quad
i=1,\dots,M\end{array}\] 考虑一组M图像\(\{x_{1},\cdot\cdot\cdot,x_{M}\}^{k}\)聚类到瓶颈空间的k个聚类,每个图像\(x_i\)与\(\{0,1\}^k\)中的标签\(y_i\)相关联。我们还使用模糊隶属度µ表示图像到k个可能的预定义簇之一的概率。输入数据x的瓶颈空间Z
(x)离质心\(c_{j}=g_{\theta}(f_{\mu}(x_{j}))\)越近,属于聚类j的x的模糊隶属度就越高。µ是模糊隶属度,m是拉格朗日乘子。然后从这个目标函数中推导出µ如下:
\[{\frac{\partial
L}{\partial\mu}}=0\Rightarrow\mu=\left({\frac{\lambda_{1}}{m\cdot\eta}}\right)^{\frac{1}{m-1}}\]
其中\(\eta=\ell[\|X_{i}-g_{\theta}(f_{\mu}(x_{j}))\|_{2}^{2}]\)。
现在我们考虑函数L的导数与在新的步骤中的权重。给定度量µ和cj是固定的,L为(8)中的最优权重w最小化
\[w_{i
j}=\exp\left[2\sum_{j=1}^{k}g_{\theta}{\big(}f_{\mu}(x_{j}){\big)}-1\right]\]
自适应熵的加入允许聚类用一个更快的迭代算法来解决分割问题。
总之,我们引入了一个用于进化无监督表示学习的DAFC。在算法1中描述了DAFC的伪代码。在每次迭代过程中,深度模糊聚类通过固定的深度FE模型和Rec模型交替选择相似和不同的样本组,并根据所选的样本组对其进行训练。具体步骤见算法1。
算法1:深度自适应模糊聚类(DAFC)
输入:数据集\(X=\{x_{i}\}_{i=1}^{k}\),平衡系数\(\lambda_{1}\)、\(\lambda_{2}\),高阈值\(\epsilon_r\)
输出:深度聚类结果R和Test_Err
1 随机初始化θ;
2 用pre_train FE模型和Rec模型初始化C、G和F;
3
\(\{A c c,A R I,N M I\}=R\);
4
重复;
5 for epoch ∈ 0, 1, .
. . , MaxEpochs do
6
生成深度ConvNets表示G;
7 for iter ∈
0, 1, . . . , MaxIter
do
8 float Max \(\mu_{i j}\) = 1;
9 \(f_{\mu}(x)\neq n u l
l\);
10 计算相似度矩阵\(C_{i,j}(\cdot)=\frac{a_{i}^{T}a_{j}}{\|a_{i}\|}\
=\frac{a_{i}^{T}a_{j}}{\sqrt{d_{i}}\sqrt{d_{j}}}\);
模糊隶属度=\(f_{\mu}\left(y_{i},x_{i}\right)=C_{i,j}\left(x_{i}\right)\cdot
y_{i}\)
11 计算\(L_{Rec}=\operatorname*{min}_{w,\theta}\sum_{i=1}^{M}\frac{1}{M}\ell\left[g_{\theta}\left(f_{w}\left(x_{i}\right)\right),f_{\mu}\left(y_{i},x_{i}\right)\right]\)
计算聚类的权值信息\(H(w)=\lambda_{1}\Biggl(1-\sum_{j=1}^{k}\mu_{i
j}\Biggr)+\lambda_{2}\sum_{i=1}^{M}\sum_{j=1}^{k}w_{i j}\log w_{i
j}\)
计算\(L_{F_{-}\mathrm{clu}}=\operatorname*{min}_{\theta,\mu,m}\sum_{i=1}^{M}\sum_{j=1}^{k}\mu_{i
j}^{m}\left\|X_{i}-g_{\theta}\bigl(f_{\mu}\bigl(x_{j}\bigr)\bigr)\right\|_{2}^{2}+H(W)\)
12 通过最小化(7)加上L
Rec和L F_clu;
13 通过最小化来更新\(\mu_{i j}\)(9);
14
while not end of R
do
15 计算设计的convnet的精度(1 -
test_error);
16 根据(10)的要求更新\(w_{i
j}\);
17 在DAFC中向FE和Rec进行反向传播;
18 直到\(\{A c c,A R I,N M
I\}=MaxR\);
19 end;
20 end;
21
return *R**,* T est_Err;
IV.实验
A.实验设置
然后,我们与IV-d中最新的深度聚类模型和传统的聚类方法进行了全面的比较。这些实验都是在cudnn
v7和RTX 2080 Ti
GPU(NVIDIA)中实现的,以测量不同深度聚类方法的性能和效率。我们考虑相同的批处理大小和相同的时代数量,以及以毫秒为单位度量推理时间。当对街景房子号(SVHN)和STL-10数据集进行训练时,我们需要注意计算所需的内存量,如果训练要在所需的时间范围内完成,也需要仔细平衡内核大小和过滤器大小。对于所有的卷积层,我们设置了不同的通道数(64、128、256和512)和滤波器大小(2×2和3×3)、步幅=1和填充=1。对于池化层,我们在最大池中设置内核大小=2和步幅=2,在平均池中设置内核大小=4和步幅=4。每一层都经过了2000次迭代的预训练,退出率为50%。我们在几个基准测试上研究了这些算法。据我们所知,我们为每个轮次设置了最大的batch_size。
本文采用了三种优化器作为优化算法。我们已经验证了当使用Adam和RMSprop优化器时的性能。与Adam和SGD相比,我们发现Adam患有通常的平衬里问题,因此给出了一个糟糕的解决方案。SGD被发现需要数千次迭代来收敛,并且也给出了一个很差的解决方案。RMSprop为在选定的复杂数据集上训练深度聚类框架提供了更精确的解决方案。此外,我们还设置了学习率(lr)=
1×10−4。为了公平地比较和清楚地说明DAFC的有效性,每种比较方法的训练期数和学习率都保持在相同的数量。我们实现了我们的方法和比较方法,并给出平均结果,以防止随机情况。
在相同的实验环境和设置下,我们还使用最优参数训练了深度自适应聚类(DAC)和深度综合相关挖掘(DCCM)。自适应参数λ被初始化为0,并在DAC中使用具有学习率lr
= 0.009的RMSprop。DCCM采用带有lr = 1e-4的RMSprop优化器,设置α = 5和β =
0.1,采用3个1×1卷积层的网络进行互信息估计鉴别器。