DeepClustering

聚类算法

​ 聚类算法是一类无监督学习算法，用于将数据分组成具有相似性的簇或群体。

传统算法

K均值聚类（K-Means Clustering）

• 优点：
  - 简单易懂，容易实现。
  - 适用于大规模数据。
  - 速度较快，适用于许多应用。
• 缺点：
  - 需要预先指定簇的数量K。
  - 对初始簇中心的选择敏感。
  - 对异常值和噪声敏感。
  - 适用于凸形簇。

层次聚类（Hierarchical Clustering）

• 优点：
  - 不需要预先指定簇的数量。
  - 可以生成层次化的簇结构。
  - 适用于不规则形状的簇。
• 缺点：
  - 计算复杂性较高，不适用于大规模数据。
  - 结果的可解释性较差。

密度聚类（Density-Based Clustering）

• 优点：
  - 能够发现任意形状的簇。
  - 对噪声和异常值相对稳健。
  - 不需要预先指定簇的数量。
• 缺点：
  - 对参数的选择敏感。
  - 不适用于数据密度差异很大的情况。

谱聚类（Spectral Clustering）

• 优点：
  - 能够发现任意形状的簇。
  - 适用于不规则形状的簇。
  - 不受初始簇中心的选择影响。
• 缺点：
  - 计算复杂性较高，对于大规模数据不适用。
  - 需要谨慎选择相似度矩阵和簇数。

DBSCAN（Density-Based Spatial Clustering of Applications with Noise）

• 优点：
  - 能够自动发现任意形状的簇。
  - 对噪声和异常值相对稳健。
  - 不需要预先指定簇的数量。
• 缺点：
  - 对于高维数据，需要特别注意参数的选择。
  - 可能在数据密度差异较大时效果不佳。

EM聚类（Expectation-Maximization Clustering）

• 优点：
  - 适用于混合模型，可以发现概率分布簇。
  - 适用于数据有缺失值的情况。

• 缺点：
  - 对初始参数的选择敏感。
  - 对于高维数据，需要特别注意参数的选择。

• 模糊聚类（Fuzzy Clustering）

• 优点：
  - 能够为每个数据点分配到多个簇，考虑数据的不确定性。
  - 适用于模糊分类问题。

• 缺点：
  - 计算复杂性较高。
  - 结果的可解释性较差。

选择适当的聚类方法通常取决于数据的性质、问题的要求以及计算资源的可用性。聚类算法可以用于数据探索、模式发现、异常检测等多种应用，但需要根据具体情况进行选择和调整。

基于网络的算法

自编码聚类算法--DEC (Deep Embedded Clustering)

1.软分配

​  使用t-SNE算法的t-分布作为核来衡量嵌入点\(z_i\)和质心\(\mu _j\)之间的相似度： \[q_{ij}=\frac{(1+\|z_i-\mu_j\|^2/\alpha)^{-\frac{\alpha+1}2}}{\sum_{j'}(1+\|z_i-\mu_{j'}\|^2/\alpha)^{-\frac{\alpha+1}2}}\] ​  其中\(z_i =f_{\theta}(x_i)\in Z\)对应于嵌入后的\(x_i\in X\)，其中\(\alpha\)是t-SNE算法t-分布的自由度，而\(q_{ij}\)可解释为将样本\(i\)分配给聚类\(j\)的概率（即软分配）。 由于我们无法在无监督的设置中对验证集上的\(\alpha\)进行交叉验证，并且得知它是多余的，因此对于所有实验，我们让\(\alpha=1\)。

2.KL分流最小化

​  使用辅助分布用来衡量样本属于某个聚类的分布，在辅助目标分布的帮助下，通过从集群的高可信度分配中学习来迭代地优化集群。具体来说，通过将软分配与目标分布匹配来训练我们的模型。为此，我们将目标定义为软分配qi和辅助分布pi之间的KL散度损失，如下所示： \[L=\mathrm{KL}(P\|Q)=\sum_i\sum_jp_{ij}\log\frac{p_{ij}}{q_{ij}}.\]

​  目标分布P的选择对于DEC的性能至关重要。一种方法是将每个pi设置为高于置信度阈值的数据点的delta分布（至最接近的质心），并忽略其余部分。但是，由于qi是软分配，因此使用较软的概率目标更为自然和灵活。
​  具体来说，我们希望我们的目标分布具有以下属性：
​  （1）加强预测（即提高簇纯度），
​  （2）更加注重以高置信度分配的数据点
​  （3）归一化每个质心的损耗贡献，以防止大型聚类扭曲隐藏的特征空间。
​  在我们的实验中，我们通过先将qi升至第二次幂，然后通过每个群集的频率进行归一化来计算pi： \[p_{ij}=\frac{q_{ij}^2/f_j}{\sum_{j'}q_{ij'}^2/f_{j'}}\\f_{j} = \sum_{i}q_{ij}\] ​  \(f_j\)为软簇频率。培训策略可以看作是一种自我培训的形式。与自训练中一样，我们采用初始分类器和未标记的数据集，然后使用分类器标记数据集，以便对其自身的高置信度预测进行训练。实际上，在实验中，我们观察到DEC通过学习高置信度预测来提高每次迭代中的初始估计，从而有助于改善低置信度预测。

3.损失的优化过程

​  我们使用带有动量的随机梯度下降（SGD）联合优化聚类中心\(\mu_j\)和DNN参数\(\theta\)。关于每个数据点zi和每个聚类质心\(\mu_j\)的特征空间嵌入的L梯度计算如下： \[\begin{aligned}\frac{\partial L}{\partial z_{i}}&=\quad\frac{\alpha+1}{\alpha}\sum_{j}(1+\frac{\|z_{i}-\mu_{j}\|^{2}}{\alpha})^{-1}\times(p_{ij}-q_{ij})(z_{i}-\mu_{j}),\\\frac{\partial L}{\partial\mu_{j}}&=\quad-\frac{\alpha+1}{\alpha}\sum_{i}(1+\frac{\|z_{i}-\mu_{j}\|^{2}}{\alpha})^{-1}\times(p_{ij}-q_{ij})(z_{i}-\mu_{j}).\end{aligned}\] ​  然后将梯度∂L/∂zi向下传递到DNN，并在标准反向传播中用于计算DNN的参数梯度∂L/∂θ。在两次连续的迭代中，当有少于tol%的点会更改聚类簇的时候，停止执行该过程。
​  第一个公式是优化AE中的Encoder参数，第二个公式是优化聚类中心。也就是说作者同时优化了聚类和DNN的相关参数。

作者设计的网络概念图如下:

img

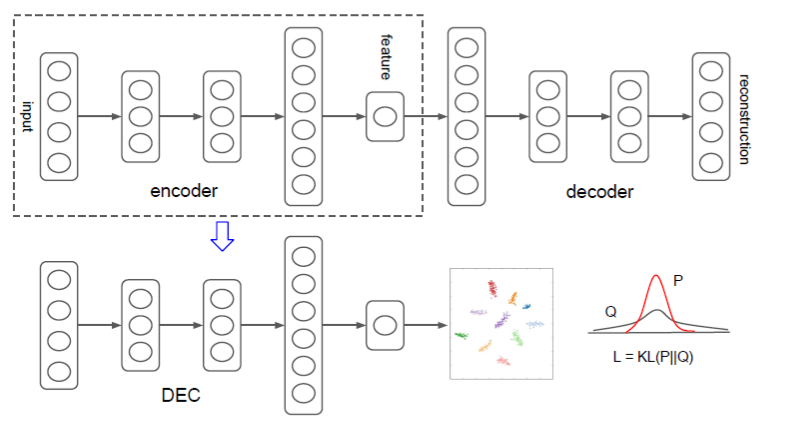
​   DEC算法由两部分组成，第一部分会预训练一个AE模型；第二部分选取AE模型中的Encoder部分，加入聚类层，使用KL散度进行训练聚类。

深度聚类

• Deep Clustering: A Comprehensive Survey
• A Survey on Deep Clustering: From the Prior Perspective
• Image Clustering with External Guidance
• Scaling Up Deep Clustering Methods Beyond ImageNet-1K
• Unsupervised Learning of Visual Features by Contrasting Cluster Assignments

Deep Clustering

(来自于Twin Contrastive Learning for Online Clustering)

​  有效的聚类策略和判别特征都是实现良好聚类的关键。由于深度神经网络强大的代表性性，深度聚类方法最近引起越来越多的关注（Asano等，2019；卡隆等，2018；郭等，2017；李等，2020,2021a；彭等人，2016；谢等人，2016；Yang等人，2016）。例如，JULE（Jangetal.，2016）迭代地学习数据表示并执行分层聚类。深度聚类（Caron et al.，2018）使用先验表示对数据进行聚类，并使用每个样本的聚类分配作为分类目标来学习新的表示。虽然表示学习和聚类可以在一定程度上相互引导，但这种两阶段的方法可能会出现在交替过程中积累的错误。这些方法的另一个缺点是，它们不能应用于在线场景，即数据以流的形式呈现，并且一次只能访问一批样本。具体来说，JULE需要全局相似性来决定应该合并哪些子集群，而Deep集群和SL（Asano et al.，2019）需要执行离线k-means或解决全局最优传输问题来获得集群分配。为了克服离线的局限性，提出了一些在线深度聚类方法（Dang等，2021；黄等，2020；吉等，2019；李等，2021b；钟等，2020）。例如，IIC（Ji等人，2019）通过最大化数据对的集群分配之间的互信息来发现集群。PICA（Huang et al.，2020）通过最大化聚类解决方案的分区置信度来学习语义上最可信的数据分离。最近，一些研究（Niu & Wang，202120；Park等人，2020；Van Gansbeke等人，2020）使用初步聚类生成的伪标签，即自标记，以多阶段方式进一步提高聚类性能。
​  与上述大多数在多个阶段执行表示学习和聚类的工作不同，我们的方法将这两个任务统一到双对比学习框架中。与之前只进行即时对比学习的研究相比，这种单阶段学习范式有助于模型学习更多有利于聚类的表征（Niu & Wang，2021；Van Gansbeke et al.，2020）。在推进阶段，尽管基于早期提取的特征修正了聚类分配（Niu & Wang，2021），但我们也可以通过单阶段学习范式，微调实例级对比学习，以减轻假阴性对的影响。

Deep Robust Clustering by Contrastive Learning

摘要

​  最近，许多无监督的深度学习方法被提出来学习与无标记数据的聚类。通过引入数据增强，大多数最新的方法从原始图像及其转换应该共享相似的语义聚类分配的角度来进行深度聚类。然而，由于softmax函数只对最大值敏感，因此，即使分配给同一集群的表示特征也可能完全不同。这可能导致表示特征空间的高类内多样性，从而导致局部最优不稳定，从而损害聚类性能。为了解决这个缺点，我们提出了深度鲁棒聚类（DRC，Deep Robust Clustering）。与现有的方法不同，DRC从语义聚类分配和表示特征两个角度进行深度聚类，可以同时增加类间多样性，减少类内多样性。与现有的方法不同，DRC从语义聚类分配和表示特征两个角度进行深度聚类，可以同时增加类间多样性，减少类内多样性。此外，我们总结了一个一般的框架，通过研究互信息和对比学习之间的内部关系，可以将任何最大化的互信息转化为最小化对比损失。我们成功地将其应用于DRC，学习不变特征和鲁棒聚类。在6个广泛采用的深度聚类基准上的广泛实验表明，DRC在稳定性和准确性方面具有优越性。例如，在CIFAR-10上达到了71.6%的平均准确率，比最先进的结果高出7.1%。

方法

问题定义

​  给定一组来自K个不同语义类的未标记图像I = {I1，...，IN }。深度聚类的目的是通过卷积神经网络（CNN）模型将图像分离为K个不同的聚类，从而将具有相同语义标签的图像简化为相同的聚类。在这里，我们旨在学习一个基于参数为θ的映射函数Φ的深度CNN网络，然后每个图像Ii都可以映射到一个k维分配特征\(z_{i}=\Phi_{\theta}(I_{i})\)。在此基础上，可以通过softmax函数得到分配概率向量pi，该函数可由 \[p_{i j}=\frac{e^{z_{i j}}}{\sum_{t=1}^{K}e^{z_{i t}}},j=1,...,K\] ​  然后可以用最大似然法预测聚类分配： \[\ell_{i}=\arg\operatorname*{max}_{j}(p_{i j}),j=1,\dots,K,i=1,\dots,N\]

网络架构

​  为了解决上述问题，我们引入了一种新的端到端深度聚类框架，同时利用分配概率和分配特征。

image-20241218212302013

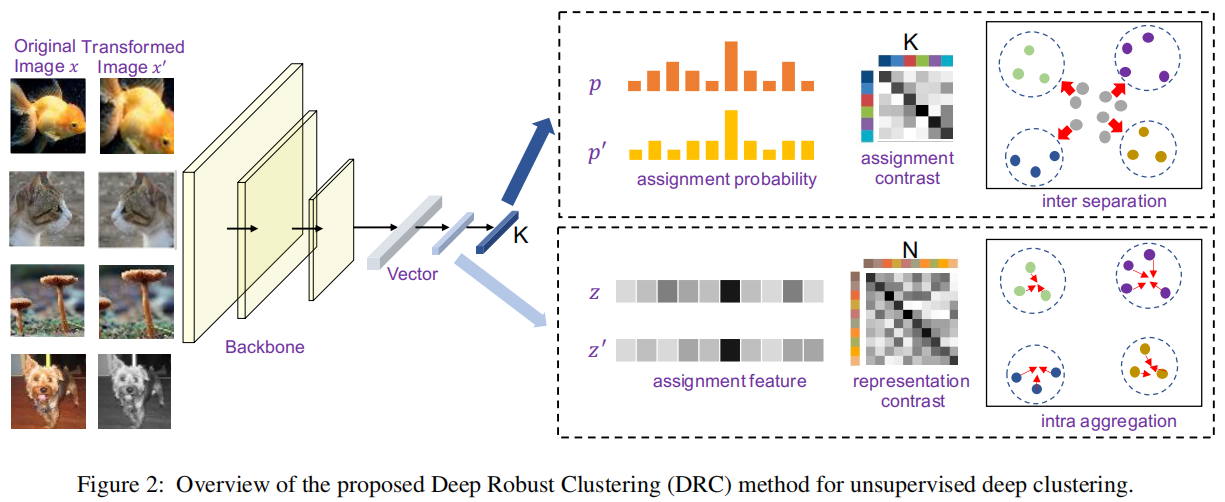
​  如图2所示，我们首先采用深度卷积神经网络（CNN）来生成K维的分配特征和分配概率。然后，利用基于分配概率的对比损失来保持原始图像及其增强图像的分配一致性，这有助于增加类间的方差，形成分离良好的聚类。利用基于分配特征的对比损失来捕获原始图像及其增强图像之间的表示一致性，有助于减少类内方差，实现更鲁棒的聚类。

互信息与对比学习

​  对比学习已被证明在无监督学习和自我监督学习中是强大的，这有助于在许多任务中实现最先进的结果。而对比损失也与互信息密切相关。设X = {x1，x2，...，xN }是一个给定空间中的N个样本。X的变换由X 0 = {x 01，x 02，...，x 0N }定义。因为我们不知道X的ground-truth，我们所知道的是，xi’都可以被视为xi的正样本，对于任何的i= 1,2，...，N。换句话说，\(p({x_{i}^{\prime}}|x_{i})\)应该比\(p({x_{j}^{\prime}}|x_{i}),j \neq i\)。一个非常自然的想法是最大限度地保留X和X'之间的互信息，定义为 \[M I({\bf X},{\bf X}^{\prime})=\sum_{i=1}^{N}\sum_{j=1}^{N}p(x_{i},x_{j}^{'})l o g{\frac{p(x_{j}^{'}|x_{i})}{p(x_{j}^{'})}}\] ​  如果我们假设 \[\frac{p(x_{j}^{'}|x_{i})}{p(x_{j}^{'})}\propto f(x_{i},x_{j}^{'})\] ​  其中f是一个在不同的情况下可能会有不同的函数，那么我们有以下定理。
定理1假设存在一个常数c0，使得\(p({x_{i}^{\prime}}|x_{i})>0\)对所有的i = 1,2，...，N都成立，那么 \[M I({\bf x},{\bf x}^{'})\geq\log N+\frac{c_{0}}{N}\sum_{i=1}^{N}\log\frac{f(x_{i},x_{i}^{'})}{\sum_{t=1}^{N}f(x_{i},x_{t}^{'})}\] ​  定义 \[\mathcal{L}_{c}=\sum_{i=1}^{N}\log\frac{f(x_{i},x_{i}^{\prime})}{\sum_{t=1}^{N}f(x_{i},x_{t}^{\prime})},\] ​  因此，最小化对比损失Lc等于最大化互信息MI（X，X 0）的下界。

损失函数

​  我们的损失函数由三个部分组成：1。一种基于分配特征的对比损失，在特征水平上保留互信息。 2. 一种基于分配概率的对比损失，使原始图像的预测标签与转换图像的预测标签之间的互信息最大化。 3. 聚类正则化损失是为了避免平凡的解。

Deep Clustering

(来自于Twin Contrastive Learning for Online Clustering)