DivClust: Controlling Diversity in Deep Clustering

Ioannis Maniadis Metaxas*, Georgios Tzimiropoulos, Ioannis Patras

Queen Mary University of London

Mile End road, E1 4NS London, UK

{i.maniadismetaxas, g.tzimiropoulos, i.patras}@qmul.ac.uk

摘要

聚类一直是机器学习领域的一个主要研究课题，深度学习最近在这个领域取得了显著的成功。然而，现有的深度聚类方法所没有解决的聚类的一个方面是，它可以有效地为给定的数据集生成多个、不同的分区。这一点尤其重要，因为一组不同的基聚类对于共识聚类是必要的，这已经被发现比依赖于单一聚类能产生更好、更鲁棒的结果。为了解决这一差距，我们提出了DivClust，一种多样性控制损失，可以纳入现有的深度聚类框架，以产生具有所需多样性程度的多个聚类。我们用多个数据集和深度聚类框架进行了实验，结果表明：a)我们的方法有效地控制多样性跨框架和数据集与非常小的额外计算成本，b)由DivClust学习到的聚类集包括解决方案明显优于单聚类基线，和c)使用现成的共识聚类算法，DivClust产生共识聚类解决方案始终优于单聚类基线，有效地提高基础深度聚类框架的性能。代码在https://github.com/ManiadisG/DivClust。

1.介绍

视觉数据量的指数级增长，随着计算能力的进步和强大的深度神经网络体系结构的发展，已经恢复了人们对使用视觉数据的无监督学习的兴趣。特别是深度聚集，这是一个近年来取得重大进展的领域。现有的工作集中于生成一个单一的聚类，这是根据该聚类与相关数据集的地面真实标签的匹配程度来评估的。然而，在深度聚类的背景下，共识或集成聚类仍有待充分研究，尽管事实上已经发现它比单一聚类结果[3,17,45,73]能持续提高性能。
共识聚类由两个阶段组成，具体生成一组基聚类，然后应用共识算法对它们进行聚合。为了在每个设置中产生更好的结果，确定集合应该拥有的属性一直是一个开放的问题[18]。然而，研究发现，集合内的聚类多样性是一个重要的、理想的因素[14,20,24,34,51]，以及个体聚类质量，多样性应该调节[15,22,51]。此外，一些研究表明，控制集合中的多样性对于研究其影响和确定其在每个设置[22,51]中的最佳水平具有重要意义。
产生不同聚类的典型方法是通过使用不同的初始化/超参数或数据[3,17]的子集对数据进行多次聚类来促进多样性。然而，这种方法并不能保证或控制多样性的程度，而且计算成本很高，特别是在深度聚类的情况下，它将需要训练多个模型。已经提出了一些方法，通过在聚类过程中包含与多样性相关的目标来发现不同的聚类，但这些方法只应用于预先计算的特征聚类，不能简单地纳入深度学习框架。其他方法通过创建和聚类不同的特征子空间来解决不同的聚类，包括一些应用于深度聚类[48,61]的方法。然而，这些方法并不能控制集群间的多样性。相反，它们通过它们所创建的子空间的属性来间接地影响它。此外，通常，现有的方法一直侧重于产生正交的聚类或基于相对简单的视觉数据的独立属性（如颜色/形状）来识别聚类。因此，它们面向最大化聚类间多样性，这不适用于共识聚类[15,22,51]。
为了解决这一差距，即利用深度聚类框架和所期望的多样性程度有效地生成多个聚类，我们提出了DivClust。我们的方法可以直接合并到现有的深度聚类框架中，以学习其多样性被明确控制的多个聚类。具体来说，该方法使用一个主干进行特征提取，然后是多个投影头，每个投影头产生聚类分配以进行相应的聚类。给定一个用户定义的多样性目标，在这项工作中，用聚类之间的平均NMI来表示，DivClust将聚类间的相似度限制在一个适当的、动态估计的阈值以下。这是通过一种新的损失组件来实现的，该组件基于模型产生的软聚类分配来估计聚类间的相似性，并惩罚超过阈值的值。重要的是，DivClust引入了最小的计算成本，并且不需要对基本的深度聚类框架进行超参数调优，这使得它的使用简单且计算效率高。
在三种深度聚类方法（IIC[37]，PICA[32]，CC[44]）（CIFAR10、CIFAR100、10）上的实验表明，DivClust可以在不降低聚类质量的情况下有效控制聚类间的多样性。此外，我们还证明，通过使用现成的共识聚类算法，DivClust学习到的不同基聚类产生了优于基框架的共识聚类解决方案，以最小的计算成本有效地改进了它们。值得注意的是，尽管共识聚类对集成的属性具有敏感性，但我们的方法在不同的多样性水平上都是稳健的，在大多数情况下表现优于基线，通常利润率很大。我们的工作为提高深度聚类框架的性能提供了一种简单的方法，同时也为研究深度聚类集成[51]中多样性的影响提供了一种新的工具。
总之，DivClust： a)可以以即插即用的方式纳入现有的深度聚类框架，计算成本非常小，b)可以显式和有效地控制聚类多样性以满足用户定义的目标，c)学习聚类，通过共识聚类提高深度聚类框架的性能。

2.相关工作

2.1.深度聚类

深度聚类是指在学习数据特征的同时对数据进行聚类的方法。它们通常分为两类，即在聚类和特征学习之间交替训练，以及同时学习。

交替学习：
采用这种方法的方法通常采用两步训练制度，定期重复进行（例如，每时代或每步）。首先，基于模型提取的表示法（例如，通过特征聚类）生成样本伪标签。其次，利用这些伪标签来改进学习到的表示，通常是通过训练特征提取模型作为一个分类器。这些方法包括DEC [64]、DAC [8]，DCCM [63]，DDC [7]，JULE [66]、SCAN [57]、ProPos [33]和SPICE [49]，以及DSC-N [36]，IDFD [65]和MIX‘EM [58]，它们提出了训练模型的方法，这些模型的表示在聚类时产生更好的结果。在这一领域的其他工作还有DeepCluster[5]、SeLa [1]、PCL [42]和HCSC [21]，尽管他们的主要重点是表示学习。

同时学习：
这些方法共同学习特征和集群分配。它们包括ADC[23]、IIC[37]和PICA[32]，它们使用损失函数端到端训练聚类模型，在集群分配上强制执行期望的属性；ConCURL[11,52]，它建立在BYOL[19]的基础上，其损失最大化了来自转换嵌入的聚类的一致性；DCCS[71]，它利用了集群过程中的一个对抗性的组件；以及GatCluster[50]，它提出了一种结合四个自学习任务的注意机制。最后，SCL[31]、CC[44]、GCC[72]、TCC[53]和MiCE[56]等方法利用了对比学习。

虽然一些深度聚类方法[1,37,52]使用了多重聚类，但大多数都没有探讨聚类间多样性的流行程度和影响，也没有人提出控制它的方法。据我们所知，我们的工作是第一个解决这两个问题的工作。

2.2.多样化聚类

生成多个不同聚类的最直接方法是多次对数据进行聚类。增加多样性的典型方法包括改变聚类算法或其超参数，使用不同的初始化，以及对样本或特征的子集进行聚类[3]。然而，这种方法a）计算成本很高，因为它需要多次对数据进行聚类，b）不可靠，因为一些增加多样性的方法可能会降低聚类的质量（例如使用数据的子集），c）无效，因为无法保证达到所需的多样性程度。
为了解决这个问题，已经提出了几种方法来创建多个、不同的聚类[25]。我们确定了两种促进聚类间多样性的主要方法： a)明确地，通过优化适当的目标，以及b)隐式地，通过优化去相关/正交特征子空间，当聚类时，会导致不同的聚类。第一类方法包括COALA [2]、Meta聚类[6]、Dec-kmeans [35]、MNMF [67]、MSC [26]、ADFT [10]和MultiCC [60]。子空间聚类方法包括MISC [59]、ISAAC [69]、NRkmeans [47]、RAOSC [70]和ENRC [48]。明显的是，OSC [9]、MVMC [68]、DMSMF [46]、DMClusts [62]、DiMSC [4]和DiMVMC [61]也在多视图数据的背景下探索了不同的聚类。
据我们所知，除了DiMVMC和ENRC之外，现有的方法都不能与深度学习兼容，它们需要一个学习的特征空间，而且大多数方法相对于样本的数量具有二次复杂度。这限制了它们在现实生活中的高维数据上的使用，其中深度聚类会产生更好的结果[56,57]。对于DiMVMC和ENRC，它们依赖于基于自动编码器的架构，并将其适应最近的深度聚类框架，其性能要好得多，这并不简单。更重要的是，它们利用子空间聚类，继承了其在控制多样性方面的局限性。具体来说： a)没有提出方法来推断不同的子空间必须为了导致特定程度的集群多样性，和b)子空间聚类方法继承聚类方法聚类算法的随机性应用于子空间（对于DiMVMC和ENRC的K-means），这进一步限制了他们对结果的控制。

2.3.共识聚类

聚类算法的性能随数据及其属性、算法本身及其超参数的不同而变化。这使得找到可靠的聚类解决方案特别困难。共识，或集成，聚类已经成为解决这个问题的一个解决方案，特别是通过组合多个，不同的聚类的结果，而不是依赖于一个单一的解决方案。这比单聚类方法[3,17,18,45]产生更好、更稳健的结果。共识聚类的过程分为两个阶段： a)生成多个、不同的基聚类，b)使用共识算法对这些聚类进行聚合。

生成不同的聚类：
共识算法所使用的聚类集的性质是获得良好性能的关键因素。[24,40,51]的多项研究发现，单个基集群的质量和多样性都是至关重要的，事实上，具有中等程度多样性的聚类集合会导致更好的结果[15,20,22]。集成生成的典型方法包括使用不同的聚类算法[13]，使用不同的初始化相同的聚类算法或不同的超参数（例如集群的数量）[16,22,41]，集群与不同的子集特征[54]，使用随机预测多样化特征空间[14]，和集群与不同数据集的子集[12,13]。然而，识别最优超参数的具体方法，如多样性的程度、集合中聚类的数量以及生成集合的方法，仍然难以捉摸。

共识算法：
共识算法的目标是聚合多个、不同的聚类，以产生一个单一的、健壮的解决方案。解决这一问题的各种方法已经被提出，如使用矩阵分解[43]，聚类[75]之间的距离最小化，利用多视图[55]，图学习[28,73,74]和矩阵协关联[29,38]。我们注意到，虽然改进共识算法总体上提高了共识聚类的鲁棒性，但集成生成的阶段及其与共识算法的聚合在很大程度上是独立的。

共识聚类和深度学习：
尽管共识聚类比单聚类方法有既定的优势，但共识聚类尚未在深度聚类的背景下被探索。一个可能的原因是生成多个、不同的基聚类的计算成本，这将需要训练多个模型。据我们所知，在深度聚类设置中应用共识聚类的唯一工作是DeepCluE [27]。值得注意的是，值得注意的是，DeepCluE使用的基聚类并不是都是由模型学习的。相反，训练单聚类模型，用U-SPEC [30]从模型的多层聚类特征生成集成。我们的工作解决了这一差距，通过提出一种方法来训练一个单一的深度聚类模型，以生成具有受控制的多样性和最小的计算开销的多个聚类。

3.方法

3.1概述：

我们的方法由两个组件组成： a)一种新的损失函数，可以纳入深度聚类框架中通过应用阈值来控制聚类间的多样性，和b)一种根据用户定义的度量动态估计该阈值以使模型学习到的聚类足够多样化的方法。

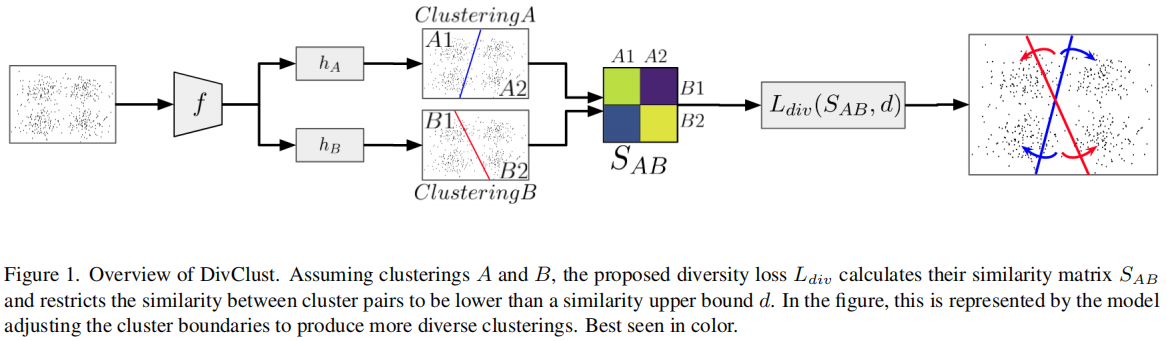
更具体地说，我们假设一个学习K聚类（通常是一个主干编码器，后面跟着K个投影头）、一个深度聚类框架及其损失函数\(L_{main}\)的深度聚类模型，和一个由用户设置的多样性目标\(D^T\)集，表示为聚类间相似性的上界1（即最大可接受的相似度）。为了控制学习聚类的聚类间相似性\(D^R\)，使\(D^{T}\leq D^{R}\)，我们提出了一个互补损失\(L_{d i v}\)。具体来说，给定一对簇\(A.B\in K\)的软集群分配，我们定义集群间相似矩阵\(S_{A B}\in\mathbb{R}^{C_{A}\times C_{B}}\)，\(C_A\)和\(C_B\)是每个集群中的集群数，和\(S_{A B}(i,j)\in[0,1]\)测量集群之间的相似性\(i\in C_{A}\)和\(j\in C_{B}\)。由此可见，降低\(S_{A B}\)的值可以减少了A簇和B簇之间的相似性，从而增加了它们的多样性。因此，\(L_{d i v}\)利用\(S_{A B}\)将聚类间的相似度限制在相似度上界d下。d值在训练过程中动态调整，\(D^{R}\gt D^{T}\)时降低，\(D^{R}\leq D^{T}\)时增加，从而收紧和放松损失函数，从而在整体和整个训练过程中，聚类间相似性\(D^{R}\)保持在或低于期望\(D^{T}\)的水平。

3.2定义聚类相似矩阵\(S_{A B}\)：

我们的方法假设一个标准的深度聚类结构，由一个编码器f，然后是K个投影头h1，...，hK，每个产生一个聚类K的赋值。具体来说，设X是N个未标记样本的集合。编码器将每个样本x∈X映射到一个表示f (x)，每个投影头hk将f (x)映射到Ck簇，这样\(p_{k}(x)=h_{k}(f(x))\in\mathbb{R}^{C_{k}\times1}\)表示一个概率分配向量，其将样本x∈X映射到聚类k中的Ck簇。在不丢失一般性的情况下，我们假设\(C=C_{k}~\forall k~\in~K\)。每个聚类都可以用聚类分配矩阵\(P_{k}(X)=[p_{k}(x_{1}),p_{k}(x_{2}),...,p_{k}(x_{N})]\in\mathbb{R}^{C\times N}\)表示。列\(p_k(n)\)，即第n个样本的概率分配向量，对样本xn被分配给不同簇的程度进行编码。行向量\(q_{k}(i)\in\mathbb{R}^{N}\)显示了哪些样本被温和地分配给聚类i∈c。我们将\(q_{k}(i)\)称为聚类隶属度向量。

为了量化聚类A和B之间的相似性，我们定义了聚类间相似性矩阵\(S_{A B}\in\mathbb{R}^{C\times C}\)。我们将每个元素\(S_{A B}(i,j)\)定义为簇\(i\in A\)的簇成员向量\(q_{A}(i)\)和簇\(j\in B\)的簇成员矢量\(q_{B}(j)\)之间的余弦相似度： \[S_{A B}(i,j)=\frac{q_{A}(i)\cdot q_{B}(j)}{||q_{A}(i)||_{2}||q_{B}(j)||_{2}}\] 这个度量表示了数据集中的样本被分配到类似于集群i和j的程度。具体来说，如果\(q_{A}(i)\perp q_{B}(j)\)，\(S_{A B}(i,j)=0\)，如果\(q_{A}(i)= q_{B}(j)\)，\(S_{A B}(i,j)=1\)。因此，它是簇i和簇j相似性的可微度量。

3.3定义损失函数：

基于聚类间相似度矩阵\(S_{A B}\)，我们定义了DivClust的损失，以温和地强制聚类A与聚类B的聚集聚类相似度不大于相似度上限d。聚合相似度\({S}_{A B}^{a g g r}\)定义为聚类A的聚类与其最相似的聚类B的聚类的平均相似性(Eq (2))。利用这个度量，我们提出了\(L_{d i v}\) (Eq(3))，该损失通过强迫\(S_{A B}^{a g g r}\lt d,\mathrm{for}\;d\in[0,1]\)来调节集群A和集群B之间的多样性。从等式3可以明显看出\(S_{A B}^{a g g r}\lt d\Rightarrow L_{d i v}(A,B)=0\)，在这种情况下，多样性要求得到满足，损失没有影响。相反，\(S_{A B}^{a g g r}\geq d\Rightarrow L_{d i v}(A,B)\gt 0\)，在这种情况下，损失要求聚类间相似性降低。 \[S_{A B}^{a g g r}=\frac{1}{C}\sum_{i=1}^{C}\operatorname*{max}_{j}(S_{A B}(i,j))\]

\[L_{d i v}(A,B)=[S_{A B}^{a g g r}-d]_{+}\]

在定义了两个聚类之间的多样性损失\(L_{d i v}\)后，我们将其扩展到多个聚类K，并将其与基础深度聚类框架的目标相结合。对于聚类k∈K，我们用\(L_{m a i n}(k)\)表示该聚类的基本深度聚类框架的损失，用\(L_{d i v}(k,k^{\prime})\)表示聚类k和聚类k’之间的多样性控制损失。我们给出了等式(4)中每个聚类k的联合损失\(L_{joint}(k)\)，其中\(L_{m a i n}(k)\)依赖于簇分配矩阵Pk，而\(L_{d i v}(k,k^{\prime})\)依赖于Pk和Pk’。因此，该模型的训练损失\(L_{total}\)，见等式(5)，是所有集群中\(L_{joint}\)的平均值。 \[L_{j o i n t}(k)=L_{m a i n}(k)+\frac{1}{K-1}\sum_{k^{\prime}=1,k^{\prime}\neq k}^{K}L_{d i v}(k,k^{\prime})\]

\[L_{t o t a l}={\frac{1}{K}}\sum_{k=1}^{K}L_{j o i n t}(k)\]

因此，损失总量是每个聚类\(k\in K\)的基深度聚类框架的损失\(L_{m a i n}\)和用于控制聚类间多样性的损失\(L_{d i v}\)的组合。所提出的损失公式适用于任何通过模型产生聚类分配的深度聚类框架（而不是使用MIX‘EM[58]的框架），它涵盖了第二节中概述的大多数深度聚类框架。

3.4动态上界d：

提出的损失\(L_{d i v}\)通过根据相似度上界d限制\(S_{AB}\)值来控制聚类间多样性。然而，\(S_{AB}\)的值是基于软簇分配的余弦相似度来计算的。这意味着成对的聚类分配向量\(i,j\)将有不同的相似度值\(S_{AB}(i,j)\)，这取决于它们的锐度，即使它们以相应的硬分配指向相同的聚类。由此可见，\(S_{AB}\)和d的影响依赖于集群分配的置信度，并在整个训练过程中和实验之间有所不同（因为集群的数量和模型容量等因素会影响集群分配的置信度）。因此，d是用户定义多样性目标的一个模糊和不直观的度量标准。
为了解决这个问题，并为定义多样性目标提供一种直观的可靠的方法，我们建议在训练过程中动态确定阈值d的值。具体地说，设D是用户选择的聚类相似度度量。在这项工作中，我们使用平均的归一化互信息（NMI），一个很好的估计聚类间相似度的度量。 \[D={\frac{1}{(K-1)(K/2)}}\sum_{k=1}^{K-1}\sum_{k^{\prime}=k+1}^{K}N\!M I(P_{k}^{h},P_{k^{\prime}}^{h})\] 其中，\(P_{k}^{h}\in\mathbb{Z}^{N}\)是聚类\(k\in K\)中N个样本的硬聚类分配向量，\(N M I(P_{k}^{h},P_{k^{\prime}}^{h})\)表示\(k\)和\(k^{\prime}\)之间的NMI。\(D\in[0,1]\)，其值越高，表示聚类程度越多。
假设用户定义的相似性目标\(D^T\)，表示为度量D的值，我们用\(D^R\)表示模型学习到的聚类的测量聚类间相似性，用相同的度量表示。DivClust的目标是控制聚类间的多样性，这转化为学习聚类，使\(D^{R}\leq D^{T}\)。因此，在训练过程中必须使用适当的阈值d。在假设\(D^R\)相对于d单调递减的情况下，我们提出了以下d的更新规则： \[d_{s+1} = \begin{cases}m a x(d_{s}(1-m),0),~~~\mathrm{if}~D^{R}\gt D^{T}\\m i n(d_{s}(1+m),1),~~~\mathrm{if}~D^{R}\le D^{T} ,\\\end{cases}\] 其中，\(d_s\)和\(d_{s+1}\)是当前和下一步步骤的阈值d的值，而\(m\in(0,1)\)调节了更新步骤的大小。根据这个更新规则，当测量的聚类间相似度\(D^R\)需要减少时，我们会减少d，否则就会增加d。为了计算效率，我们不是在每个训练步骤中计算整个数据集的\(D^R\)，而是在M=10000集群分配的内存库中每20次迭代一次——后者以FIFO方式更新。我们在所有实验中将超参数m设置为m = 0.01。

4.实验

5.讨论

5.1.多样性控制和共识聚类性能

5.2.复杂性和计算成本

6.结论

我们引入了DivClust，这是一种可以整合到现有的深度聚类框架中的方法，可以在控制聚类间多样性的同时学习多个聚类。据我们所知，这是第一种可以基于用户定义的目标明确控制间聚类多样性的方法，并且与学习特性和端到端聚类聚类的深度聚类框架兼容。我们的实验，使用多个数据集和深度聚类框架进行，证实了DivClust在控制聚类间多样性及其适应性方面的有效性，因为它可以兼容各种框架，而不需要修改和/或超参数调优。此外，结果表明，DivClust学习了高质量的聚类，在共识聚类的背景下，与单一聚类基线和替代集成聚类方法相比，这导致了提高的性能。