Efficient Deep Embedded Subspace Clustering

$\begin{gathered} \mathrm{Jinyu~Cai}^{1,3},\mathrm{~Jicong~Fan}^{2,3*},\mathrm{Wenzhong~Guo}^{1},\mathrm{~Shiping~Wang}^{1},\mathrm{~Yunhe~Zhang}^{1},\mathrm{~Zhao~Zhang}^{4} \\ \text{College of Computer and Data Science, Fuzhou University, China} \\ \text{2School of Data Science, The Chinese University of Hong Kong (Shenzhen), China} \\ \text{'Shenzhen Research Institute of Big Data, China }^4\text{Hefei University of Technology, China} \\ \{jinyucai1995,cszzhang\}@gmail.com,fanjicong@cuhk.edu.cn \\ \mathrm{guowenzhong@fzu.edu.cn,\{shipingwangphd,zhangyhannie\}@163.com} \end{gathered}$

摘要

最近，深度学习方法在数据聚类任务方面取得了重大进展。深度聚类方法（包括基于距离的方法和基于子空间的方法）将聚类和特征学习集成到一个统一的框架中，在那里聚类和表示之间存在相互促进。然而，深度子空间聚类方法通常在自表达模型的框架内，具有二次时间和空间复杂性，阻碍了其在大规模聚类和实时聚类中的应用。在本文中，我们提出了一种新的深度聚类机制。我们的目标是以迭代细化的方式从深度表示中学习子空间基，而细化的子空间基则帮助学习深度神经网络的表示。该方法脱离了自表达框架，可以线性地扩展到样本大小，适用于任意大的数据集和在线聚类场景。更重要的是，该方法的聚类精度远远高于其竞争对手。在基准数据集上与最先进的聚类方法进行的广泛比较研究，证明了该方法的优越性。

1. 引言

聚类是机器学习中的一个基本问题，它的目的是在没有标签信息的情况下，在高类内相似度和低类间相似度的要求下，将样本分离成类。许多经典的聚类算法如k-means [29]和谱聚类（SC）[30]在实际应用中取得了巨大的成功。然而，它们在处理具有复杂结构或/和高维性的数据时并不有效，这可以通过使用数据的细化特征来改进。事实上，[14,37,38,47]之前的一些工作利用了特征学习技术，如非负矩阵分解[2]、自动编码器（AE）[1]及其变体[24,31,36]来学习低维嵌入进行聚类，从而提高了聚类的精度。然而，由于这些方法是两阶段聚类，并且特征学习不是针对聚类的，因此不能保证学习到的表示适合于聚类。
近年来，一些研究人员提出了端到端聚类方法，如深度嵌入式聚类（DEC）[40]、联合无监督学习（JULE）[41]、深度自适应聚类（DAC）[6]和深度综合相关挖掘（DCCM）[39]。在这些方法中，聚类目标与网络优化过程相结合，这提供了一种学习面向聚类的嵌入式表示的方法。然而，大多数深度聚类方法使用基于欧几里德距离的度量来识别聚类，而欧几里德距离对于不同类型的数据结构并不总是有效或合理的。
子空间聚类假设数据位于不同的子空间[11]中。稀疏子空间聚类（SSC聚类）[11]和低秩表示（LRR）[27]主要基于光谱聚类[30]，优于k均值聚类和经典光谱聚类。最近，一些研究人员[8,21,25,44]表明，联合子空间聚类和深度学习在基准数据集上有很好的性能。然而，这些方法很难扩展到大规模的数据集，因为它们需要学习一个自我表达的矩阵，从而导致二次时间和空间的复杂度。因此，[12,48,49]的一些最新工作致力于提高子空间聚类的效率。
在本文中，我们旨在提供一种高效和精确的深子空间聚类的方法。我们提出从深度自动编码器提取的潜在特征中学习一组子空间基，其中的基和网络参数被迭代细化。我们提出从深度自动编码器提取的潜在特征中学习一组子空间基，其中的基和网络参数被迭代细化。该方法的网络结构如图1所示。

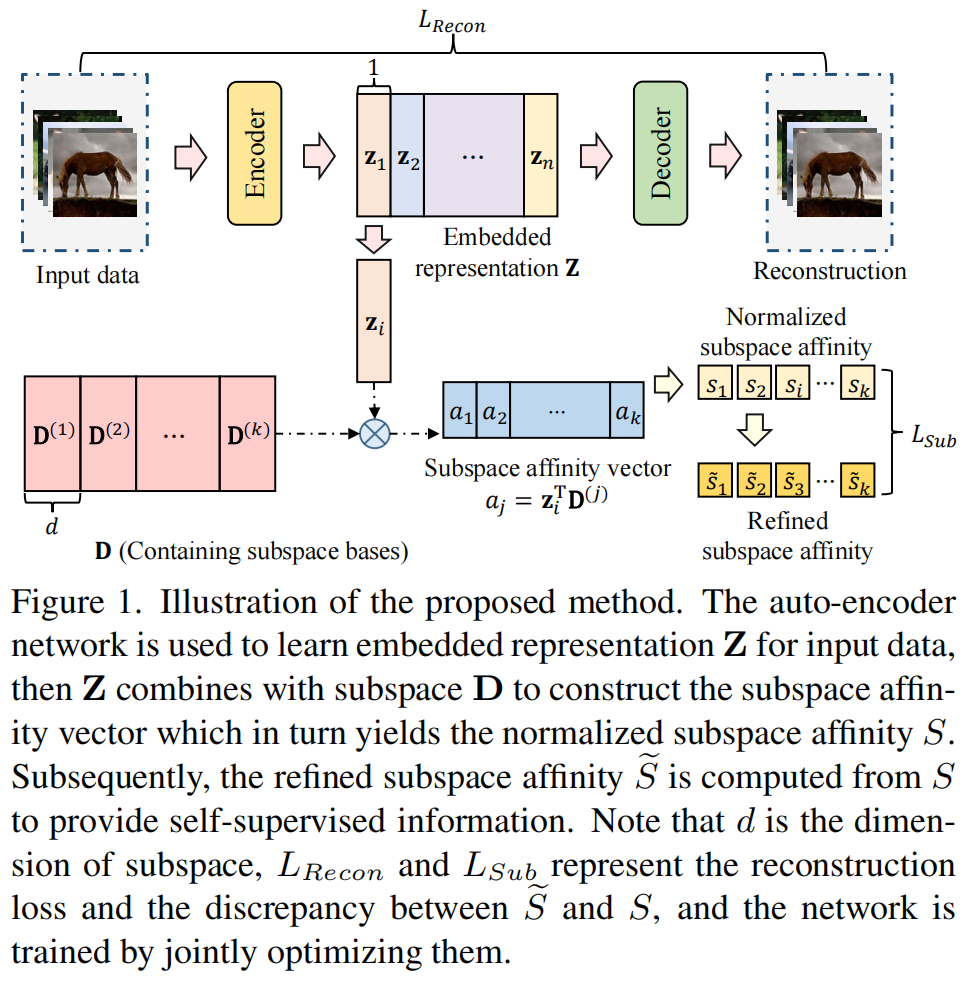
图1.提出方法的说明。利用自动编码器网络学习输入数据的嵌入式表示Z，然后Z与子空间D结合构造子空间相似度向量，得到归一化的子空间相似度$S$。然后，从$S$计算细化的子空间相似度$\widetilde{S}$，提供自监督信息。注意，$d$是子空间的维数，$L_{Recon}$和$L_{Sub}$表示重构损失和$\widetilde{S}$与$S$之间的差异，并通过联合优化它们来训练网络。

我们的贡献如下：

我们提出了一种新的脱离传统的自我表达框架的深度子空间聚类方法
该方法具有线性的时间和空间复杂度，因此适用于大规模的子空间聚类。
我们将该方法推广到在线聚类，从而可以有效地处理任意大的数据集和流数据集。
分析了利用深度神经网络转换基于距离的聚类和子空间聚类的可行性。

在许多基准数据集（如Fashion-MNIST、STL-10和REUTERS-10k）上的数值结果表明，我们的方法比其竞争对手更有效。

2. 相关工作及简要讨论

2.1 深度聚类

早期的深度聚类方法旨在应用深度特征学习方法（如自动编码器[36]和变分自动编码器（VAE）[24]）从复杂的高维数据中提取特征进行聚类。然而，这些解决方案很难学习适合于聚类任务的表示。目前的深度聚类方法侧重于构建端到端模型。Xie等人提出了DEC [40]，设计了一个基于t-SNE [35]设计的聚类目标。它提供了一个实现聚类中心和嵌入式特征同步优化的聚类模型。Chang等人[5]提出了深度自我进化聚类（DSEC），这是一种基于自我进化的算法，用所选择的模式对交替训练网络。在[39]中，Wu等人提出了一种名为DCCM的方法，该方法使用伪标签进行自我监督，并使用互信息来捕获更多有区别的表示用于聚类。由Huang等人[20]提出的分区置信度最大化（PICA）使分区不确定性指数最小化，并学习了最有信心的聚类分配。请注意，这些深度聚类方法使用欧氏距离来分配聚类，当聚类不集中于平均值时，这可能没有用处。

2.2 子空间聚类

经典的子空间聚类，如SSC [11]，LRR [27]，Kernel-SSC [32]，旨在学习光谱聚类的自表达相似度矩阵。Ji等人[21]提出了深度子空间聚类网络（DSC-Net），该网络包含了一个具有自编码器网络的自表达模块。与SSC和LRR相比，DSC-Net在多个图像数据集上都有了显著的改进。Zhou等人[52]提供了一种称为深度对抗性子空间聚类（DASC）的方法，该方法利用生成的对抗性网络[16]提供对抗性学习，提高了深度子空间聚类的性能。Zhou等人[51]提出了分布保留的子空间聚类（DPSC）来保留子空间中的潜在分布，以提高子空间聚类模型的特征学习能力。另一方面，一些研究者试图降低子空间聚类[7,12,13,33,49]的复杂性。例如，Zhang等[49]提出了k-子空间聚类网络（k-SCN），将子空间的更新整合到嵌入式空间的学习中，以解决学习相似度矩阵的缺点。Fan [12]提出了一种k-分解子空间聚类（k-FSC）方法，该方法具有线性的时间和空间复杂度，能够处理缺失数据和流数据。

2.3 简短的讨论

我们分析了表1中经典子空间聚类、大规模子空间聚类和深度子空间聚类等几种（由于空间限制）方法的时空复杂性。

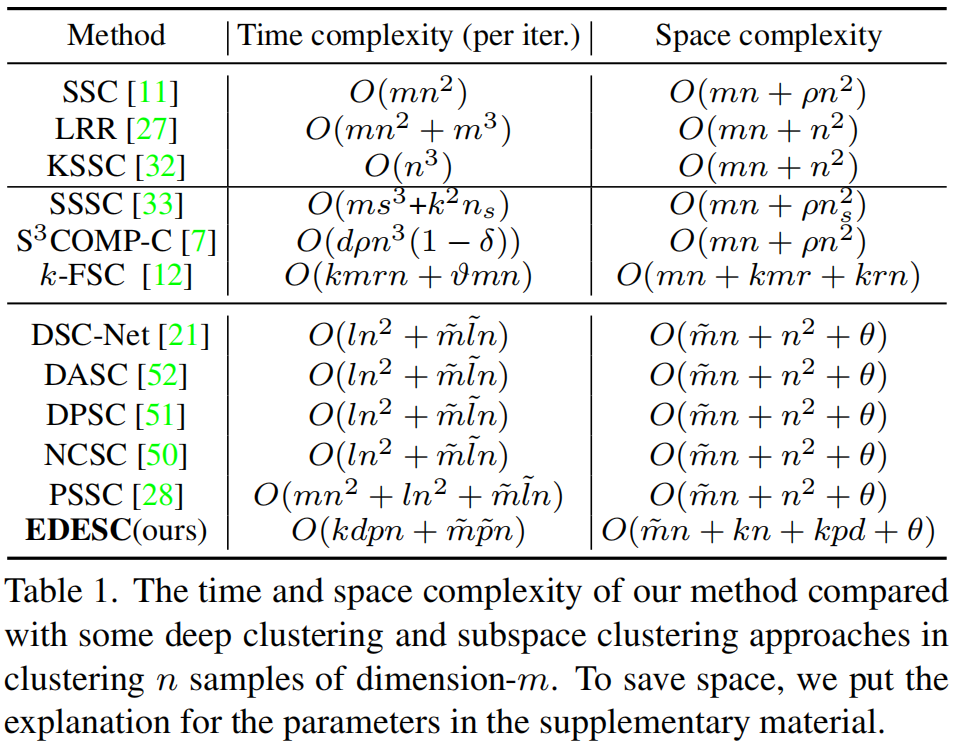
表1.该方法与一些深度聚类和子空间聚类方法在聚类n个样本的维度为m中的时间复杂度和空间复杂度比较。为了节省空间，我们在补充材料中加入了对参数的解释。

我们可以看到，这些经典的子空间聚类方法和深度子空间聚类方法在样本数量上具有二次时间和空间的复杂性。相比之下，我们的方法具有线性的时间和空间复杂度，可与[12]的大规模子空间聚类方法相媲美。

3. 方法

3.1 提出的模型

在本文中，我们主要针对基于深度学习的子空间聚类，并试图解决以下问题。

问题1

给定一个数据矩阵$\mathbf{X}\in\mathbb{R}^{m\times n}$，其中$m$表示特征数，$n$表示样本数。假设$\mathrm{X=\bar{X}P}$，其中$\bar{X}=[\bar{\mathbf{X}}^{(1)},\bar{\mathbf{X}}^{(2)},\ldots,\bar{\mathbf{X}}^{(k)}]$和$\mathbf{P}\in\mathbb{R}^{n\times n}$是一个未知排列的矩阵。对于$j=1,\ldots,k$，假设$\bar{\mathbf{X}}^{(j)}\in\mathbb{R}^{m\times n_j}$的列是由以下得来： \[\mathbf{x}=\mathbf{f}_j(\mathbf{v})+\varepsilon,\] 其中$\mathbf{f}_j:\mathbb{R}^{r_k}\longrightarrow\mathbb{R}^m$是一个未知的非线性函数，$r_{j}<m$，$\mathbf{v}\in\mathbb{R}^{r_{j}}$是一个随机变量，$\varepsilon\in\mathbb{R}^{m}$表示随机高斯噪声。从$\mathrm{X}$中找到排列矩阵$\mathrm{P}$（或等价的$\bar{X}$）。这个问题正是一个聚类问题，为此我们需要将$\mathrm{X}$的列分组成k个聚类，对应于k个不同的函数$\mathbf{f}_{1},\ldots,\mathbf{f}_{k}$。

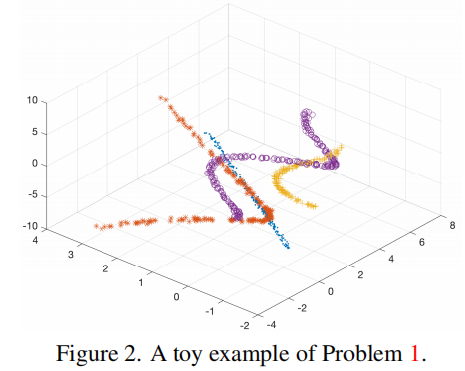
图2显示了$m=1$和$r_{1}=\cdots=r_{5}=1$的一个简单例子。注意，当$\mathbf{f}_{1},\ldots,\mathbf{f}_{k}$都是线性的，这个问题简化为经典的子空间聚类。
问题2

在问题1中，对于$j=1,\ldots,k$，假设$\mathbf{f}_{j}(\mathbf{v})=\mathbf{g}(\mathbf{B}^{(j)}\mathbf{v})$，其中$\mathbf{B}^{(j)}\in\mathbb{R}^{p\times r_j}$和$\mathbf{g}:\mathbb{R}^p\longrightarrow \mathbb{R}^m$。此外，$\frac{\|\mathbf{B}^{(i)^{\top}}\mathbf{B}^{(j)}\|_{F}}{\|\mathbf{B}^{( i)}\|_{F}\|\mathbf{B}^{( j )}\|_{F}}(i\neq j)$足够小。从$\mathrm{X}$中找到排列矩阵$\mathrm{P}$（或等价的$\bar{X}$）。

问题2比问题1更容易，因为当我们获得$\{\mathbf{B}^{(1)},\ldots,\mathbf{B}^{(k)}\}$的良好估计时，就识别出正确的集群足够了。因此，在本文中，首先，我们提出通过用多层神经网络近似$x$来估计$B^{(j)}$，即： \[\mathbf{x}_i\approx h_\mathcal{W}(\hat{\mathbf{B}}^{(j)}\hat{\mathbf{v}}_i), \mathbf{x}_i\in\mathbb{C}_j,\] 其中，$h_\mathcal{W}$为参数集为$\mathcal{W}$的多层神经网络，$\mathbb{C}_j$为第$j$个聚类。很难直接获得$\{\hat{\mathbf{B}}^{(1),}\ldots,\hat{\mathbf{B}}^{(k)}\}$。相反，我们估计了$\mathbf{B}^{(j)}\mathbf{V}_i$，即$\mathbf{z}_{i}:=\hat{\mathbf{B}}^{(j)}\hat{\mathbf{v}}_{i}$。因此，我们提出优化去解决： \[\begin{aligned}\operatorname*{minimize}_{\mathcal{W},\{\mathbf{z}_{1},\ldots,\mathbf{z}_{n}\}}&\frac{1}{2n}\sum_{i=1}^{n}\|\mathbf{x}_{i}-h_{\mathcal{W}}(\mathbf{z}_{i})\|^{2},\\\mathrm{subject~to~}&\mathbf{z}_{i}\in\mathbb{S}_{i}, i=1,\ldots,n,\end{aligned}\] 其中，$\mathbb{S}_{i}$表示真正的簇$\mathbf{x}_{i}$应该属于的簇。然而，不可能直接解决(3)，因为$\mathbb{S}_{i}$是未知的。现在我们引入了一个新的变量$\mathbf{D}=[\mathbf{D}^{(1)},\mathbf{D}^{(2)},\ldots,\mathbf{D}^{(k)}]$。它包含$k$个块和$\mathbf{D}^{(j)}\in \mathbb{R}^{p\times d}$，$ |_{u}^{{(j)}|=1$，$u=1,,d$，$j=1,,k$。注意，对于所有的$j=1,,k$，$dr_{j}$。我们希望$}{(j)}$与$^{{(j)}$，$j=1,,k$有相同的列空间。然后根据我们在问题2中所做的假设，对于所有的$jl$，$|}{(j)^}{(l)}|_F$都足够小，即：$$\|\mathbf{D}^{(j)^\top}\mathbf{D}^{(l)}\|_F\leq\tau, j\neq l,$$ 其中，$\tau$是一个很小的常数。
表示$\alpha_{i}=\mathrm{arg~max}_{j}\|\mathbf{z}_{i}^{\top}\mathbf{D}^{(j)}\|$。我们期待： \[\|\mathbf{z}_i^\top\mathbf{D}^{(\alpha_i)}\|\gg\max_{j\neq\alpha_i}\|\mathbf{z}_i^\top\mathbf{D}^{(j)}\|, i=1,\ldots,n.\] 换句话说，$\mathbf{z}_{i}$只与$\mathbf{D}$的一个块高度相关。现在我们使用一个参数集为$\mathcal{W}^{\prime}$的编码器$h_{\mathcal{W}^{\prime}}^{\prime}$来表示$\mathbf{z}_{i}$，即： \[\mathbf{z}_i=h'_{\mathcal{W}'}(\mathbf{x}_i), i=1,\ldots,n.\] 为了方便起见，我们让： \[\hat{\mathbf{x}}_i:=h_{\mathcal{W}}(\mathbf{z}_i), i=1,\ldots,n.\] 和表示$\hat{\mathbf{X}} = [\hat{\mathbf{x}}_{1},\ldots,\hat{\mathbf{x}}_{n}]$。现在，我们把(3)、(4)、(5)、(6)和(7)一起解决 \[\begin{alignat}{2}&\operatorname*{minimize}_{\mathcal{W},\mathcal{W}^{\prime},\mathbf{D}} & \quad & \frac{1}{2n}\left\|\mathbf{X}-\hat{\mathbf{X}}\right\|_{F}^{2}, \\&\text{subject to} & & \|\mathbf{D}_{u}^{(j)}\|=1, \; u=1,\ldots,d, \; j=1,\ldots,k, \nonumber \\& & & \|\mathbf{D}^{(j)} \mathbf{D}^{(l)}\|_{F}\leq\tau, \; j\neq l, \nonumber \\& & & \|\mathbf{z}_{i}^{\top}\mathbf{D}^{(\alpha_{i})}\|\gg\max_{j\neq\alpha_{i}}\|\mathbf{z}_{i}^{\top}\mathbf{D}^{(j)}\|, \; i=1,\ldots,n. \nonumber\end{alignat}\] 注意，在(8)中，$\mathbf{z}_{i}$只是根据(6)中的中间变量，我们不需要显式地优化它们。在(8)中，第一个约束是控制$\mathbf{D}$的列的大小，否则$\left\|\mathbf{z}_i^\top\mathbf{D}^{(\alpha_i)}\right\|$可能变为零。第二个约束是为了符合问题1中不同子空间之间不相似的假设。最后一个约束起着子空间分配的作用。请注意，我们的方法(8)仍然适用于问题1，前提是神经网络能够学习一个$\mathbf{g}(\mathbf{B}^{(j)}\mathbf{v})$来有效地近似问题1中的$\mathbf{f}_j(\mathbf{v})$。

3.2 实用的解决方案

现在我们将展示如何近似地求解(8)。为了方便起见，我们让 \[L_{Recon}=\frac{1}{2n}\sum_{i=1}^{n}\left\|\mathbf{x}_{i}-\mathbf{\hat{x}}_{i}\right\|_{F}^{2}.\] 我们通过最小化以下目标，在(8)中施加第一个约束 \[D_{Cons1}:=\frac12\left\|\mathbf{D}^\top\mathbf{D}\odot\mathbf{I}-\mathbf{I}\right\|_F^2,\] 其中$\odot$表示阿达玛积，$\mathbf{I}$是大小为$kd$的$kd$的单位矩阵。
对于(8)中的第二个约束，我们进行了定义 \[\begin{gathered}D_{Cons2}:= \begin{aligned}\frac{1}{2}\left\|\mathbf{D}^{(j)\top}\mathbf{D}^{(l)}\right\|_{F}^{2}, j\neq l,\end{aligned} \\\text{=} \frac12\left\|\mathbf{D}^\top\mathbf{D}\odot\mathbf{O}\right\|_F^2. \end{gathered}\] 这里的$\mathbf{O}$是一个矩阵，其中所有$d$大小的对角线块元素都是0，其他所有元素都是1。现在我们可以把（10）和（11）放在一起，得到$\mathbf{D}$上的正则化项 \[D_{Cons}=\xi(D_{Cons1}+D_{Cons2}),\] 其中，$\xi$是一个在本工作中固定在$10^{−3}$的调优参数。
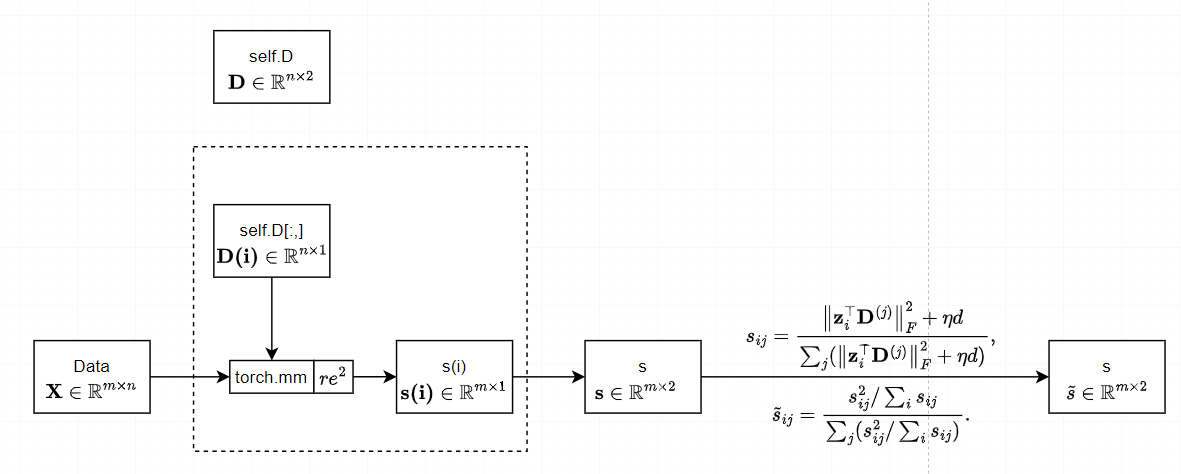
对于(8)中的最后一个约束，我们提出了一种新的子空间相似度矩阵$S$来度量嵌入表示$\mathbf{Z}$和子空间基代理$\mathbf{D}$之间的关系 \[s_{ij}=\frac{\left\|\mathbf{z}_i^\top\mathbf{D}^{(j)}\right\|_F^2+\eta d}{\sum_j(\left\|\mathbf{z}_i^\top\mathbf{D}^{(j)}\right\|_F^2+\eta d)},\] 其中，$\eta$是一个控制平滑度的参数。因此，$s_{ij}$表示嵌入式表示$\mathbf{z}_{i}$属于由$\mathbf{D}^{(j)}$表示的第$j$个子空间的概率。我们进一步引入了一个由定义的细化子空间相似度矩阵$\widetilde{S}$： \[\widetilde{s}_{ij}=\frac{s_{ij}^2/\sum_is_{ij}}{\sum_j(s_{ij}^2/\sum_is_{ij})}.\] 换句话说，$\widetilde{S}$可以作为一种自监督信息，从而产生以下子空间聚类目标： \[L_{Sub}=KL(\widetilde{S} || S)=\sum_{i}\sum_{j}\widetilde{s}_{ij}\log\frac{\widetilde{s}_{ij}}{s_{ij}}.\] 现在我们将(8)的无约束松弛定义为 \[L=L_{Recon}+D_{Cons}+\beta L_{Sub}.\] 在算法1中给出了该方法的训练流程。

该方法实现了子空间聚类和嵌入式表示学习的联合优化。$\mathbf{D}$的初始化由预训练模型的$\mathbf{Z}$上的k-means生成的簇的列空间给出。当对网络的训练完成后，最终的聚类结果可以通过一下得到： \[\mathcal{C}_i=\arg\max_js_{ij}.\]

3.3 通用的近似和转换问题

有人可能会认为，神经网络具有普遍的逼近能力，因此可以将子空间聚类问题转换为基于距离的聚类问题，从而应用k-means和DEC [40]，或者可以将基于距离的聚类问题转换为子空间聚类问题。在这里，我们生成了两个合成数据集来显示转换的执行方式。第一个数据集是用于基于距离的聚类，并且 \[\mathbf{x}_{i}^{(j)}\sim\mathcal{N}(\mu_{j},\mathbf{I}), i=1,\ldots,1000,\\\mu_{j}\in\mathbb{R}^{m}, \mu_{j}\sim\mathcal{U}(-1,1),\] 然后是$\mathbf{x}_i^{(j)}\longleftarrow\sin(\mathbf{x}_i^{(j)})$，其中$m = 100$和$j=1,\ldots,10$。第二个数据集是用于子空间聚类的，并且 \[\mathbf{x}_{i}^{(j)}=\sin(\mathbf{B}^{(j)}\mathbf{v}_{i}), \mathbf{v}_{i}\sim\mathcal{N}(\mathbf{0},\mathbf{I}), i=1,\ldots,1000,\\\mathbf{B}^{(j)}\in\mathbb{R}^{m\times p}, \mathbf{B}^{(j)}\sim\mathcal{N}(\mathbf{0},\mathbf{I}),\] 其中，$m = 100$，$p = 2$，和$j=1,\ldots,10$。我们还向数据集上添加了高斯噪声，即$\mathrm{X}\leftarrow\mathrm{X}+\mathrm{N}$，其中噪声的标准误差是干净$\mathrm{X}$的标准误差的0.2倍。
DEC [40]、IDEC [18]和我们的方法的性能如图3所示。

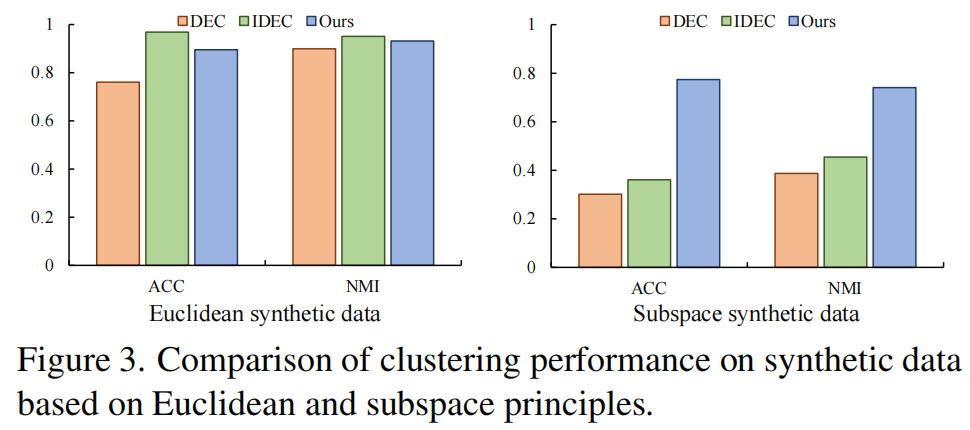
第一个图表明，将基于距离的聚类问题转换为子空间聚类问题相对容易，因为我们的方法的精度相当高。第二个图表明，DEC和IDEC失败，将子空间聚类问题转换为基于距离的聚类问题非常困难。一个可能的原因是，将欧几里德距离（例如$\|\mathbf{u}_1-\mathbf{u}_2\|$）转换为子空间相似度（例如$\mathbf{v}_{1}^\top\mathbf{v}_{2}$）更容易。例如，设$\mathbf{v}_1=\phi(\mathbf{u}_1)$和$\mathbf v_{2}=\phi(\mathbf u_{2})$，其中$\phi$是径向基函数的特征图，例如高斯核。然后我们有 \[\mathbf{v}_1^\top\mathbf{v}_2=\exp(-\gamma\|\mathbf{u}_1-\mathbf{u}_2\|^2),\] 其中，$\gamma>0$是一个超参数。因此，神经网络只需要学习一个$\phi$的近似值，这并不困难。如果我们交换u和v的角色，网络需要学习一个函数$h$，这样$\|h(\mathbf{v}_1)-h(\mathbf{v}_2)\|$是$\|\mathbf{v}_1^\top\mathbf{v}_2\|$的单调（大致）变换，这是相当困难的。
以上结果和分析验证表明，有必要提供一种有效、准确的深度子空间聚类方法来更普遍地处理问题2或问题1。