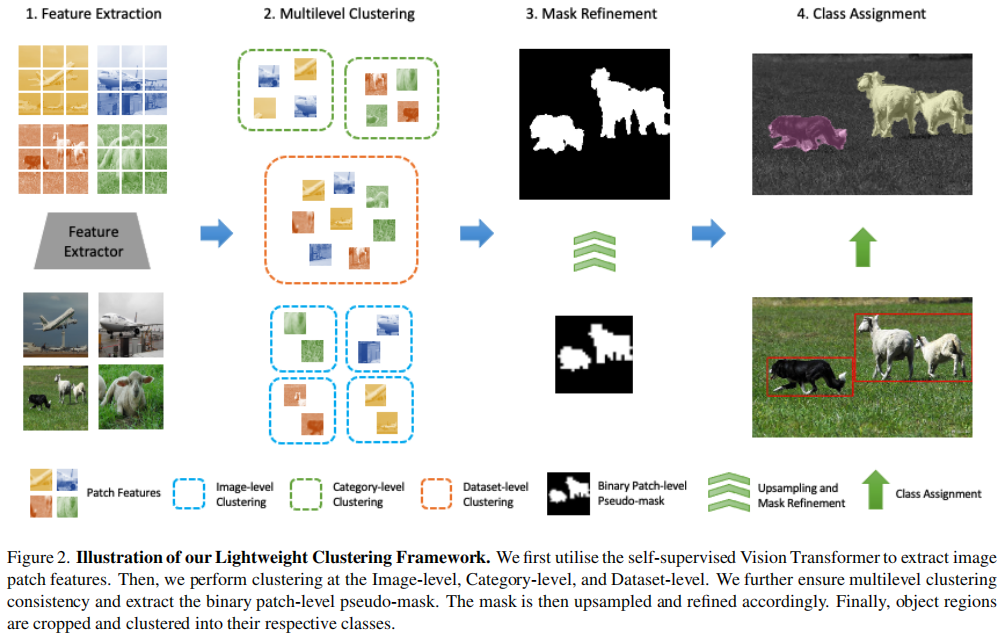
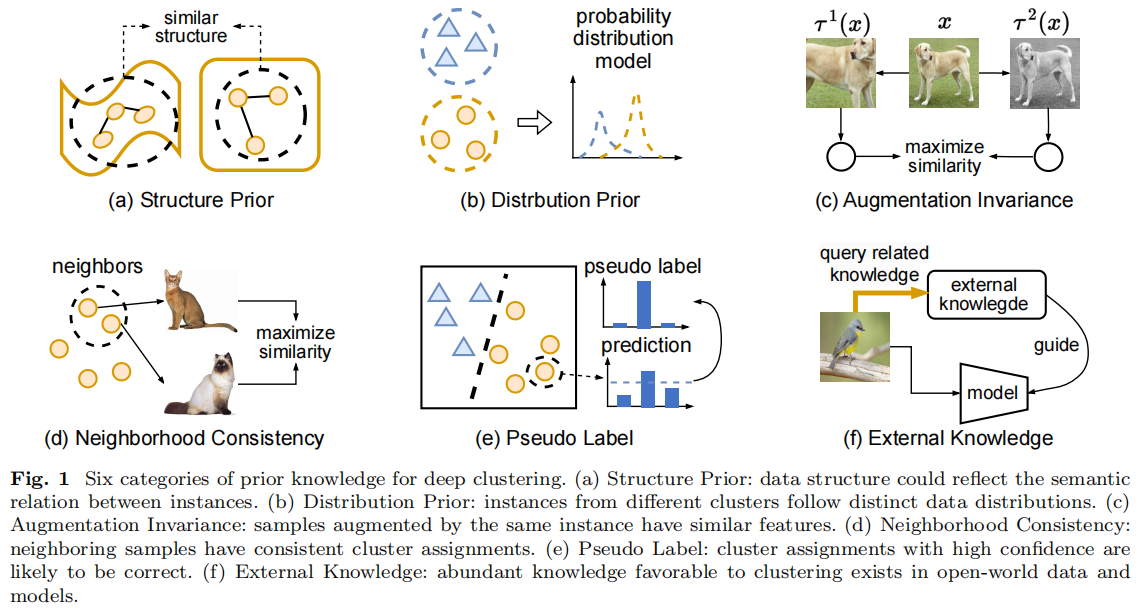
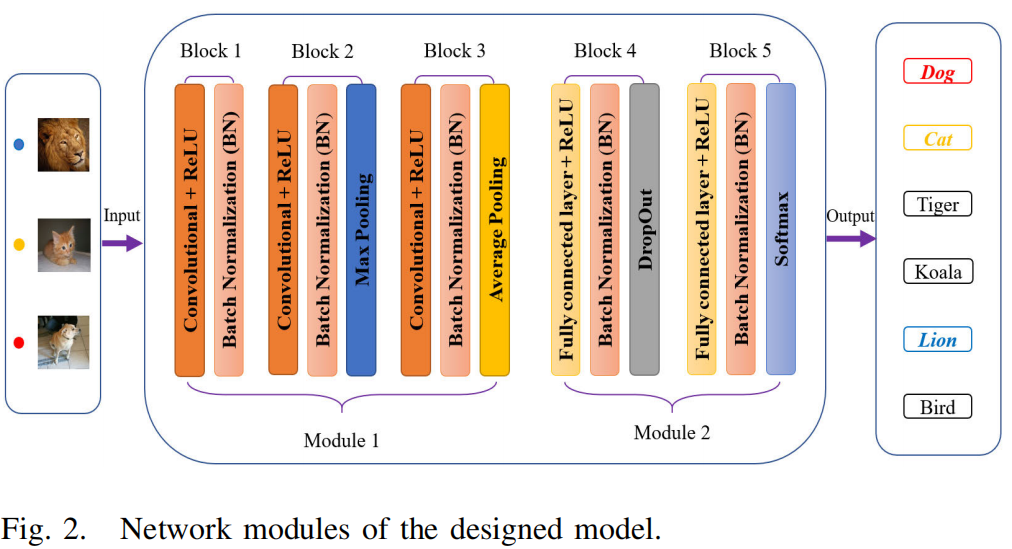
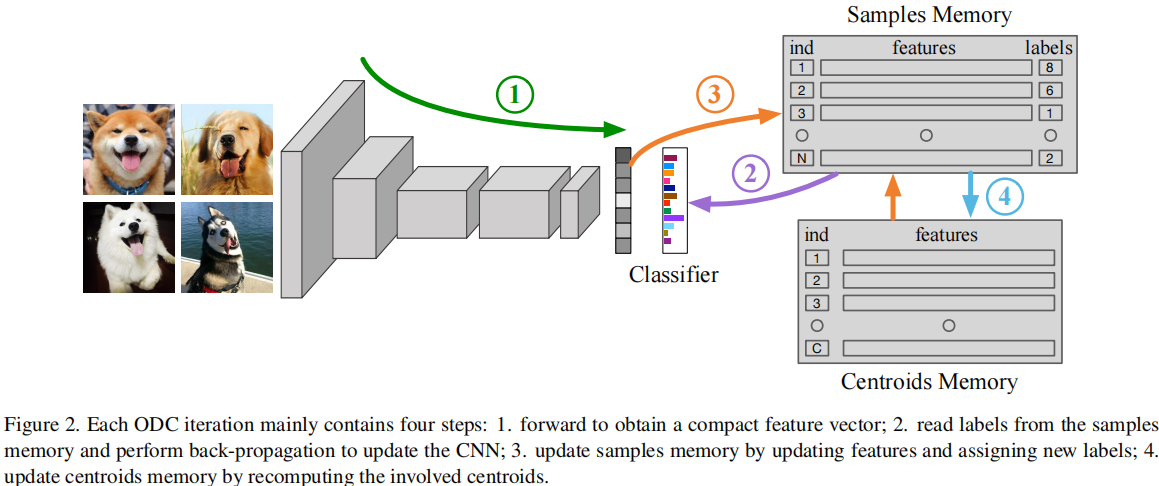
End-to-end Differentiable Clustering with Associative Memories

End-to-end Differentiable Clustering with Associative Memories

Bishwajit Saha 1 Dmitry Krotov 2 Mohammed J. Zaki 1 Parikshit Ram 2 3

摘要

​  聚类是一种广泛使用的无监督学习技术，涉及到一个密集的离散优化问题。联想记忆模型或AMs是一种可微的神经网络，定义了一个递归动力系统，它已与各种深度学习架构集成。我们揭示了AM(Associative Memory)动力学和聚类中所需的固有离散分配之间的新联系，提出了一种新的无约束的连续松弛问题，使端到端可微聚类，称为ClAM(clustering with AM)。利用AMs的模式完成能力，我们进一步开发了一种新的自监督聚类损失。我们对不同数据集的评估表明，ClAM受益于自监督，并显著改进了传统的Lloyd‘s k-means算法和最近的连续聚类松弛（剪影系数高达60%）。

1. 引言

​  最近，传统的联想记忆或AM模型(Hopfield, 1982; 1984)被重新制定，以显著提高其记忆存储容量，并与现代深度学习技术集成(Krotov & Hopfield, 2016; Ramsauer et al., 2020; Krotov & Hopfield, 2021; Krotov, 2021)。这些新模型被称为密集联想记忆（Dense Associative Memories），是完全可微的系统，能够在突触权重中存储大量的多维向量，称为模式或“记忆”。它们可以使用反向传播算法在端到端完全可微的设置中进行训练，通常带有自监督损失。
​  我们认为，这种以端到端可微的方式学习AM的突触权值的能力，以及每个数据点恰好指向一个记忆的离散分配（关联），使AM唯一适合于可微聚类的任务。我们在图1中给出了一个简单的结果，其中标准的基于原型的聚类方案（离散的和可微的）无法找到正确的聚类，但我们提出的基于AM的方案是成功的。具体来说，我们做出了以下贡献：

• 我们开发一个灵活的数学框架集群AM或ClAM，这是一个新颖的连续无约束放松的离散优化问题，允许集群端到端可微的方式，同时保持整个训练的离散集群分配，与线性时间集群分配。
• 我们利用AMs的模式完成能力来开发一个可区分的自监督损失，以提高聚类质量。
• 我们的经验证明，ClAM能够持续提高k-means高达60%，可以同时与基于光谱的聚类方法和与基于凝聚的聚类方法竞争，并产生深刻的解释。

2.相关工作

​  离散聚类算法
​  聚类是一个固有的硬组合优化问题。基于原型的聚类公式，如k-means聚类是np困难的，即使是对于k = 2（Dasgupta，2008）。然而，广泛使用的Lloyd’s算法或Voronoi迭代方法（Lloyd，1982）可以相当有效地找到局部最优解，这可以通过多次重启和仔细的迭代来改进(Vassilvitskii & Arthur, 2006)。它是一种直观的离散算法，在A（根据当前原型诱导的Voronoi分区（Aurenhammer，1991）为集群的分配点）和B（基于当前集群分配更新原型点）之间交替使用。然而，该方案的离散性质使其难以逃脱任何局部最小值。我们认为，基于SGD的原型聚类能够通过逃避局部最小值来提高集群的质量，同时也继承了SGD的计算效率。光谱聚类公式（Donath &霍夫曼，1973；Von Luxburg，2007）利用点的成对相似性或亲和性的特征谱（用图拉普拉斯式表示）将数据划分为“连接组件”，但没有明确地提取每个聚类的原型。这允许光谱聚类以Voronoi分区不允许的方式对数据进行分区。然而，它天真地需要二次时间（点数）来生成拉普拉斯矩阵，也需要三次时间来进行谱分解。层次聚类（Johnson，1967）基于先前建立的聚类找到连续的聚类，以自上而下的方式将它们划分，或以自下而上的方式进行组合。这些离散分层算法天真地在点的数量，尽管一些形式的自下而上的凝聚方案可以显示在二次（Sibson，1973）甚至次二次时间（3月等，2010）利用双树算法（Ram等人，2009；Curtin等人，2013；2015）。

​  密度聚类方案
​  如流行的DBSCAN（酯等，1996）和SNN（阿吉拉尔等，2001），不认为集群作为离散优化问题，但发现的问题模式数据分布，允许任意形状的集群鲁棒性噪声和异常值（桑德et al.，1998）。然而，多维密度估计是一项具有挑战性的任务，特别是使用非参数方法（西尔弗曼，1986；Ram & Gray，2011），导致使用参数模型，如高斯混合模型（雷诺兹，2009）（可以从期望最大化的数据中估计（Dempster et al.，1977））。

​  可微深度聚类
​  可微性在深度聚类中至关重要，我们希望同时学习点的潜在表示，并在该潜在空间中执行聚类(Ren et al., 2022;Zhou et al., 2022)。现有的可微聚类公式，如范数和（Panahi et al.，2017）或非负矩阵分解（Kim & Park，2008），本质上是解决约束优化，不直接适合端到端可微深度学习管道。因此，各种方案利用了某种形式的软聚类公式，如模糊k-均值（Bezdek et al.，1984）。Xie等人（2016）提出了一种新的概率k-means公式，启发于t-SNE（Minton，2008），对预先训练的自编码器（AE）的表示进行可微聚类（DEC），Guo et al. (2017a) （IDEC）显示了从联合学习表征和聚类中获得的收益。对于图像深度聚类中的表示学习，Song等人（2013）、Xie等人（2016）和Yang等人（2017）使用了堆叠自动编码器，Guo等人（2017b）（DCEC）使用卷积自动编码器（CAE）进行了进一步的改进。Chazan等人（2019年）使用了多个AEs，每个聚类一个，但（软）聚类分配是使用模糊k-means进行的。Cai等人（2022）在DEC放松中增加了一个“焦点损失”，以惩罚非离散任务，同时也增强了表征学习。深度子空间聚类（Peng等人，2016；Ji等人，2017；Zhang等人，2019）放宽了组合光谱聚类问题（同样采用部分聚类分配），并利用“self-expressive”层以可微的方式同时学习必要的拉普拉斯矩阵（相似度矩阵）和聚类。因此，深度聚类通常使用一些概率部分分配的点给多个簇，偏离了原始k-means的离散性质。此外，这些方案通常利用通过Lloyd（1982）进行的预先训练过的AEs和/或k-means来初始化网络参数。我们提出的ClAM保持了聚类的离散分配性质，并且在没有任何特殊播种的情况下工作良好。

​  联想记忆（AM）
​  这是一个神经网络，它可以存储一组多维向量-记忆-作为一个循环动态系统的定点吸引子状态。它被设计为将初始状态（呈现给系统）与固定点（内存）上的最终状态关联起来，从而定义吸引力的不相交盆地或数据域的分区，因此可以表示聚类。该网络在数学上被形式化为经典的Hopfield网络（霍普菲尔德，1982），但已知其内存容量有限，只能在d维数据域中存储≈0.14d随机内存（Amit等人，1985；McEliece等人，1987）。对于相关数据，容量甚至更小，并且通常会导致一个不动点将整个数据集吸引到单个盆地中。对于相关数据，容量甚至更小，并且通常会导致一个不动点将整个数据集吸引到单个盆地中。这种行为对于集群来说是有问题的，因为集群的数量——稳定的固定点的数量——应该与数据维数解耦。Krotov & Hopfield（2016）提出了现代霍普菲尔德网络或密集AM，通过在动态系统中引入快速增长的非线性激活函数，允许更密集的内存排列，以及超线性(d)内存容量。对于某些激活函数，致密AMs具有幂律甚至指数容量（克罗托夫&霍普菲尔德，2016；德米西吉尔等人，2017；拉姆索尔等人，2020年；卢西贝罗和梅扎德，2023年）。Ramsauer等人（2020）证明了变压器的注意机制（Vaswani等人，2017）是具有软max激活的密集AMs的一种特殊极限情况。密集的AMs也被用于描述整个变压器块（Hoover等人，2023年），以及集成在复杂的基于能量的神经结构中（Hoover等人，2022年）。对这些结果的回顾见Krotov（2023）。密集的AMs最近也被研究与缝线连接（Burns & Fukai，2023），并应用于异质结合环境（Liang et al.，2022）。在我们的工作中，我们将证明密集算法的循环动态和大内存容量使它们唯一适合聚类。

3.集群中的联想记忆

​  在本节中，我们提出了(i)基于AMs的ClAM的数学框架，（ii）激发了其对聚类的适用性，以及（iii）提出了一种学习记忆的方法，以进行良好的聚类。我们将所有这些放在我们的新的基于原型的聚类算法ClAM中。

3.1.联想记忆：数学框架

​  在d维欧几里得空间中，考虑M内存${\mathit{\rho }}_{\mu }\in {\mathbb{R}}^d,\mu \in [M]\triangleq \{1,\dots ,M\}$（我们稍后将讨论记忆是如何学习的）。这个数学框架的关键方面是能量函数和attractor dynamics(Krotov & Hopfield, 2021; Millidge et al., 2022)。一个适合聚类的能量应该是一个点（或一个粒子）$v\in {\mathbb{R}}^d$的连续函数。此外，能量应该有M个局部最小值，对应于每个内存。最后，当一个粒子逐渐接近一个记忆时，它的能量应该主要由单个记忆决定，而剩余的M−1记忆的贡献应该很小。一个满足这些要求的能量函数为： $$\begin{array}{}\text{(1)}& E(\mathit{v})=-\frac{1}{\beta }\log (\sum _{\mu \in [M]}\exp (-\beta \Vert {\mathit{\rho }}_{\mu }-\mathit{v}{\Vert }^2))\end{array}$$ ​  用一个标量的$\beta >0$被解释为一个逆的“温度”。随着$\beta$的增长，方程1中的exp（·）确保只有前导项仍然显著，而其余的M−1项被抑制。因此，整个能量函数将用最近记忆周围的抛物线来描述。该空间将被划分为每个记忆周围的M个吸引盆地，每个记忆周围的能量函数的形状将主要由最近的记忆来定义，并对其他记忆进行了小的修正。
​  attractor dynamics通过dv/dt控制v在时间内空间中的移动，同时确保能量减少。这就是dE (v)/dt < 0，它确保了一个粒子收敛到一个局部最小值——动力学的一个不动点。attractor dynamics可以通过能量景观上的梯度下降来描述： $$\begin{array}{}\text{(2)}& \tau \frac{d\mathit{v}}{dt}=-\frac{1}{2}{\mathrm{\nabla }}_{\mathit{v}}E=\sum _{\mu \in [M]}({\rho }_{\mu }-\mathit{v})\mathit{\sigma }(-\beta \Vert {\rho }_{\mu }-\mathit{v}{\Vert }^2)\end{array}$$ ​  其中$\tau >0$是一个特征时间常数，描述了粒子在能量景观上移动的速度，$\sigma (\cdot )$是对记忆缩放距离的softmax函数，定义为$\sigma (z_{\mu })=\exp (z_{\mu })/\sum _{m=1}^M\exp (z_m)$的任何$\mu \in [M]$。这一点如图2a所示。这就保证会减少能量 $$\begin{array}{}\text{(3)}& \frac{dE(\mathit{v})}{dt}\stackrel{(\mathbf{a})}{=}{\mathrm{\nabla }}_{\mathit{v}}E(\mathit{v})\cdot \frac{d\mathit{v}}{dt}\stackrel{(\mathbf{b})}{=}-2\tau \Vert \frac{d\mathit{v}}{dt}{\Vert }^2\stackrel{(\mathbf{c})}{\le }0\end{array}$$ ​  其中(a)为链式规则，(b)遵循方程2，(c)中的等式表示局部平稳性。在一个离散的时间步长t+1下，对于点v从状态$v_t$到$v^{t+1}=v^t+{\delta }^{t+1}$的有效更新${\delta }^{t+1}$是通过有限差分： $$\begin{array}{}\text{(4)}& {\delta }^{t+1}=\frac{dt}{\tau }\sum _{\mu \in [M]}({\rho }_{\mu }-v^t)\sigma (-\beta \Vert {\rho }_{\mu }-v^t{\Vert }^2)\end{array}$$ ​  给定一个点S的数据集，对于每个点v∈S，我们可以用一些噪声破坏它，从而产生一个扭曲的点v˜。这可以作为AM网络v0←v˜的初始状态。AM动态是由可学习的权重ρµ，µ=1，…，M，它也对应于动态（记忆）的固定点。根据方程4，T递归的网络随时间演化，其中选择T以确保充分收敛到一个固定点（见图2b中的例子）。将最终状态vT与未损坏的v进行比较来定义损失函数 $$\begin{gathered} \begin{array}{}\text{(5)}& \mathcal{L}=\sum _{\mathit{v}\in S}\Vert \mathit{v}-{\mathit{v}}^T{\Vert }^2 \\ \mathrm{where}{\mathit{v}}^0\leftarrow \tilde{\mathit{v}}\end{array} \end{gathered}$$ ​  相对于AM参数ρµ，它的反向传播最小。在集群的背景下，AM模型自然诱导一个分区的数据空间不重叠盆地的吸引力，隐式定义了一个硬集群分配定点在每个盆地，并通过完全连续的和可微的动态，允许学习与标准深度学习框架，我们接下来讨论。

3.2.AM作为一个可微离散arg min求解器

​  考虑具有数据集$S\subset {\mathbb{R}}^d$的原始k-means目标，其中我们学习k个原型$R\triangleq \{{\rho }_{\mu },\mu \in [k]\}$与$[k]\triangleq \{1,\cdot \cdot ,k\}$通过解决以下问题： $$\begin{gathered} \begin{array}{}\text{(6)}& \underset{R}{min}\sum _{\mathit{x}\in S}\Vert \mathit{x}-{\mathit{\rho }}_{{\mu }_{\mathit{x}}^{\star }}{\Vert }^2 \\ \text{s.t.}{\mu }_{\mathit{x}}^{\star }=\arg \underset{\mu \in [k]}{min}\Vert \mathit{x}-{\mathit{\rho }}_{\mu }{\Vert }^2\end{array} \end{gathered}$$ ​  ${\mu }_x^{\star }$（对于每个x）的离散选择使方程6成为一个不能通过（随机）直接解决梯度下降的组合优化问题。这个问题的一个常见的连续松弛方法如下： $$\begin{array}{}\text{(7)}& \underset{R}{\min }\sum _{x\in S}\sum _{\mu \in [k]}{w}_{\mu }(x){\Vert x-{\rho }_{\mu }\Vert }^2\end{array}$$ ​  其中（通常）$w_{\mu }(x)\in [0,1]$和$\sum {}_{\mu \in [k]}{w}_{\mu }(x)=1,\mathrm{\forall }x\in S$。因此，这些权重$\{w_{\mu }(x),\mu \in [k]\}$定义k原型的概率，并设计在最接近的原型${\rho }_{{\mu }_x^{\ast }}$，并在剩余的原型上尽可能小。例如，具有到原型的距离的softmax函数$\sigma (\cdot )$已被用作$w_{\mu }(x)=\sigma (-\gamma \Vert \alpha -{\rho }_{\mu }{\Vert }^2)$，其中，$\gamma >0$是一个超参数，并作为$\gamma \to \mathrm{\infty },$，$\sum _{\mu \in [k]}{w_{\mu }(x)\Vert x-{\rho }_{\mu }||}^2\to {\Vert x-{\rho }_{{\mu }_x^{\ast }}\Vert }^2$。其他加权函数也开发出具有类似的特性（Xie et al.，2016），本质上利用了到学习原型的距离的加权和，从而在本质上与在原始问题中的离散分配${\mu }_x^{\star }$不同（方程6）。另一个微妙的点是，在所有原型上训练时对任何x∈S的软加权分配与推理时对最近原型的硬聚类分配不匹配，这导致了训练和推理之间的不一致。
​  我们提出了一个新的替代连续松弛方法来解决离散k均值问题，利用AM动力学（3.1），在k均值目标中保持离散分配。给定原型（内存）$R=\{{\rho }_{\mu },\mu \in [k]\}$，动力学（方程2）和更新（方程4）确保任何例子（粒子）x∈Rd将收敛到一个原型${\rho }_{{\hat{\mathit{\mu }}}_x}$对应的一个盆地，如果我们设置$x^0\leftarrow x$和对T时间步长的x0应用公式4中的更新，那么$x^T\approx {\rho }_{{\hat{\mu }}_x}$。此外，对于适当的β，${\hat{\mu }}_x$匹配k-means目标中的离散分配${\mu }_x^{\ast }$（公式6）。
​  这意味着，对于适当设置β和T，$x^T\approx {\rho }_{{\mu }_x^{\ast }}$，允许我们取代所需的每个例子损失$\Vert x-{\rho }_{{\mu }_z^{\ast }}{\Vert }^2$目标$\Vert x-x^T{\Vert }^2$，允许我们重写k意味着（方程6）以下连续优化问题： $$\begin{gathered} \begin{array}{}\text{(8)}& \underset{R}{min}\sum _{x\in S}{\Vert x-x_R^T\Vert }^2 \\ \mathrm{where}{x}^0\leftarrow x\end{array} \end{gathered}$$ ​  其中，$x_R^T$是通过T递归步骤对任何x∈S进行更新得到的，下标“R”突出了对原型R的依赖性。
​  通过上面的讨论，方程8中的目标对原始k-means目标（方程6）具有期望的离散分配，因为$x_R^T$恰好收敛到其中一个原型。与现有的“加权和”方法相比，这是k-均值目标的一个显著不同的放松。这种松弛的紧密性依赖于β（逆温度）和T（递归深度）的选择——我们将它们视为超参数，并以一种依赖于数据的方式来选择它们。对于任何给定的β和T，我们可以通过通过时间的反向传播，用SGD（和变量）最小化方程8。

3.3.理解由AMs引起的分区

3.4.ClAM：聚类 与AMs和自我监督

​  接下来，我们希望利用上述AMs（3.1）的强大模式完成能力。我们使用标准掩膜自我监督学习——我们应用（随机）掩膜$m\in \{0,1{\}}^d$到点$x\in S\subset {\mathbb{R}}^{\overline{d}}$和利用上e递归完成部分模式$x^0=m\odot x$和ground-truth之间的失真掩盖值和完成模式我们的损失如下: $$\begin{array}{}\text{(9)}& \mathcal{L}=\sum _{x\in S}{\mathbb{E}}_{m\sim \mathcal{M}}\Vert \overline{m}\odot (x-x_R^T){\Vert }^2,x^0\leftarrow m\odot x\end{array}$$ ​  其中$x_R^T$由$x^0$演变而来，方程4的T递归。原型R是通过SGD最小化自监督模式完成损失（方程9）来学习的。精确的学习算法在算法1的TrainClAM子程序中给出，并如图5所示。

image-20241007095524047

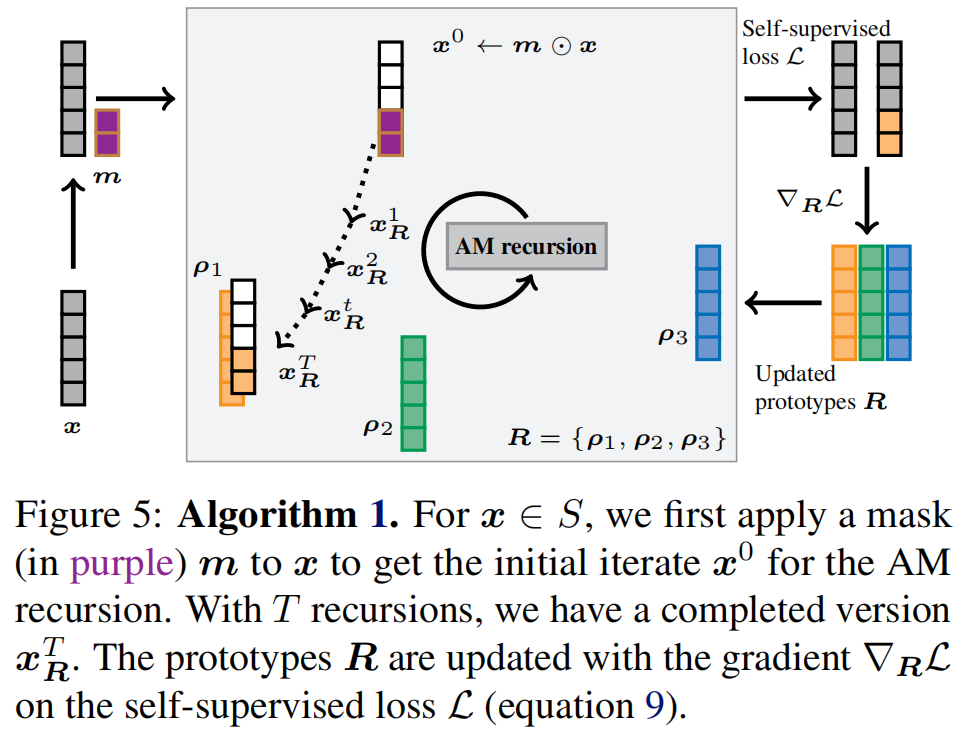
图5：算法1。对于x∈S，我们首先应用一个掩码（紫色的）m到x来得到AM递归的初始迭代x0。对于T递归，我们有一个完整的版本x T R。原型R用自监督损失L上的梯度∇RL进行更新（公式9）。

​  在随机播种原型（第2行）之后，我们对数据（第3行）（数据批B中的每个x），我们应用随机掩码（第8行），使用当前原型（第9-12行）完成AM递归的模式，累积公式9（第13行），并使用批梯度（第14行）更新原型。

image-20241006230200990

​  命题3.1：算法1中的TrainClAM子例程占用$O(dkTN|S|)$时间，其中$|S|$是S的基数，收敛到一个$O(N^{-1/2})$-平稳点。
​  $N^{-1/2}$项来自于光滑非凸问题的标准SGD的收敛速度（内斯特罗夫，2003），可以通过动量改进到$N^{-3/2}$（Fang等人，2018），考虑到我们的提出的端到端可微性，这是很简单的。算法1的InferClAM子程序使用学习到的原型R分配集群，并一次通过S。这在聚类结束时调用一次。
​  命题3.2：算法1中的InferClAM子例程需要占用$O(dkTN|S|)$时间，其中$|S|$是S的基数。
​  从命题3.1和3.2中，我们可以看到，ClAM训练和推理在数据集S中的点$|S|$数、维数d和簇数k上是线性的。对于数据集S上的N个时期，ClAM训练取$O(dkTN|S|)$，其中T为AM递归深度，而k-means训练（采用Lloyd算法）取$O(dkN|S|)$。因此，k-means和ClAM都与点数成线性关系，尽管ClAM运行时有一个乘法系数T，其中T通常小于10。所以k-means直觉上比ClAM快。需要注意的是，k-means和ClAM明显高于谱聚类和凝聚聚类，凝聚聚类的样本数量通常在二次和三次之间。注意，对于相同数量的时代，我们可以为基于SGD的ClAM建立收敛保证（这可以通过使用基于动量的SGD来改进），而k-means没有类似的收敛保证。

（wei'wan）