1.Twin Contrastive Learning for Online Clustering

摘要

本文提出通过在实例和聚类水平上进行双对比学习（TCL）来进行在线聚类。具体来说，我们发现当数据投影到目标簇数维数的特征空间时，其特征矩阵的行和列分别对应于实例和聚类表示。基于观察，对于给定的数据集，提出的TCL首先通过数据增强构造正对和负对。然后，在特征矩阵的行空间和列空间中，分别通过将正对推开，进行实例级和聚类级对比学习。为了减轻内在假阴性对的影响和校正聚类分配，我们采用了一个基于置信度的标准来选择伪标记，以提高实例级和聚类级的对比学习。从而进一步提高了聚类性能。除了双对比学习的优雅理念外，TCL的另一个优点是，它可以独立地预测每个实例的聚类分配，从而毫不费力地拟合在线场景。在6个广泛使用的图像和文本基准上进行的广泛实验证明了TCL的有效性。该代码将在GitHub上发布。

1介绍

在本研究中，我们基于图1所示的观察结果，提出了一种基于双对比学习（TCL）的端到端在线深度聚类方法。

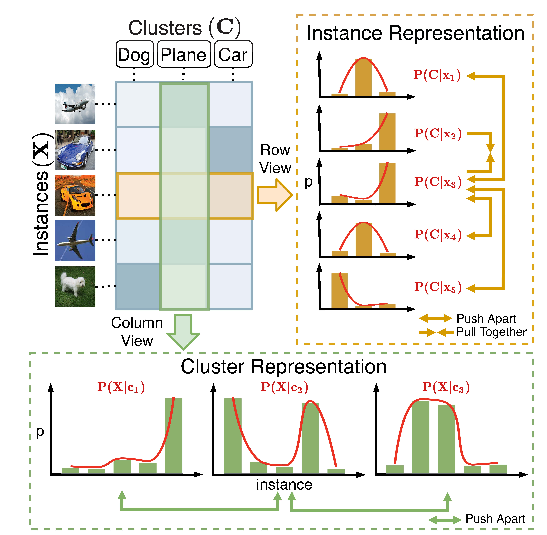
图1：我们的主要观察结果和基本思想。通过将数据投影到维数为簇数的特征空间中，特征矩阵的第i行和第k列中的元素表示实例i属于聚类k的概率。即，行对应于集群分配概率，这是实例的特殊表示。更有趣的是，如果我们从列视图中看特征矩阵，每一列实际上对应于数据上的集群分布，这可以看作是集群的一种特殊表示。因此，可以分别在行级、列空间和列空间中进行实例级和集群级的表示学习（例如，对比学习）。

简而言之，特征矩阵的行和列分别对应于实例表示和簇表示。在此基础上，TCL对特征矩阵的行空间和列空间进行对比学习，共同学习实例和聚类表示。具体来说，TCL首先通过数据扩充来构造对比对。与大多数现有的使用SimCLR中提出的弱增强的对比学习方法不同（Chen et al.，2020a）不同，我们提供了一种新的混合有效增强策略。对于构建的对，TCL在实例和聚类水平上进行对比学习。实例级对比学习的目的是将不包含的实例拉在一起，同时将类之间的实例分开。聚类级对比学习的目的是区分不同聚类的分布，同时吸引不同增强下的分布。为了减轻内在假阴性对的影响并纠正聚类分配，我们逐步选择可信的预测（即那些聚类分配概率接近一热的预测）来对双对比学习进行微调。这种微调策略是基于以下观察，即具有高可信度的预测更有可能是正确的，因此可以用作伪标签。一旦模型收敛，它就可以以端到端方式独立地对每个实例进行集群分配，以实现集群。本工作的主要贡献总结如下：

我们揭示了特征矩阵的行和列在本质上对应于实例和集群表示。在此基础上，我们提出了通过在实例和聚类水平上同时进行对比学习来实现聚类的TCL；
我们提供了一种新的数据增强策略，通过混合弱转换和强转换，它自然适合我们的TCL框架，并在我们的实验中被证明对图像和文本数据都是有效的；
为了减轻内在假阴性的影响和校正聚类分配，我们采用了一个基于置信度的准则来生成伪标签，以便对实例级和聚类级的对比学习进行微调。实验结果表明，这种微调策略可以进一步提高聚类性能；
提出的TCL以端到端和在线的方式对数据进行集群，只需要批优化，因此可以处理大规模数据集。此外，TCL可以处理流数据，因为它可以及时地为新的数据进行集群分配，而不访问整个数据集。

2相关工作

虽然对比学习和深度聚类的结合带来了很好的结果，但大多数现有的工作仍然是分开处理这两个任务的。与现有的研究不同，本研究优雅地将对比学习和深度聚类统一到双对比学习框架中，这可能会给两个社区带来一些见解。值得注意的是，本研究是（Li et al.，2021b）的一个重要扩展，有以下改进：

在本文中，我们提出了一种基于置信度的增强策略来微调实例级和聚类级的对比学习。具体来说，大多数混杂预测被选择作为伪标签是基于观察到它们更有可能是正确的。在此基础上，我们利用生成的伪标签来缓解实例级对比学习中假阴性对（由类内样本组成）的影响，并在聚类级对比学习中采用交叉熵损失来校正聚类分配。值得注意的是，这种双自我训练范式受益于我们的TCL框架，因为实例特征（来自ICH）的集群分配（来自CCH）可以通过在线方式获得。
在本文中，我们提出了一种通过混合弱转换和强转换的数据增强策略。虽然这种增强策略看起来很简单，但其有效性与所提出的TCL框架密切相关。先前的研究表明，直接在对比学习框架中引入强增强可能会导致次优表现（Wang and Qi，2021）。与此结论不同的是，我们表明混合增强策略自然适合所提出的TCL框架（更多细节见表6）。
为了研究该方法的泛化能力，我们验证了我们的方法在文本聚类中的有效性，尽管在数据增强方面存在差异。实验结果表明，所提出的TCL框架、混合增强策略和基于置信度的增强策略具有优越性。与之前的会议论文相比（Li等人，2021b），该期刊扩展获得了类似的性能提高。

3方法

提出的TCL的管道如图2所示。

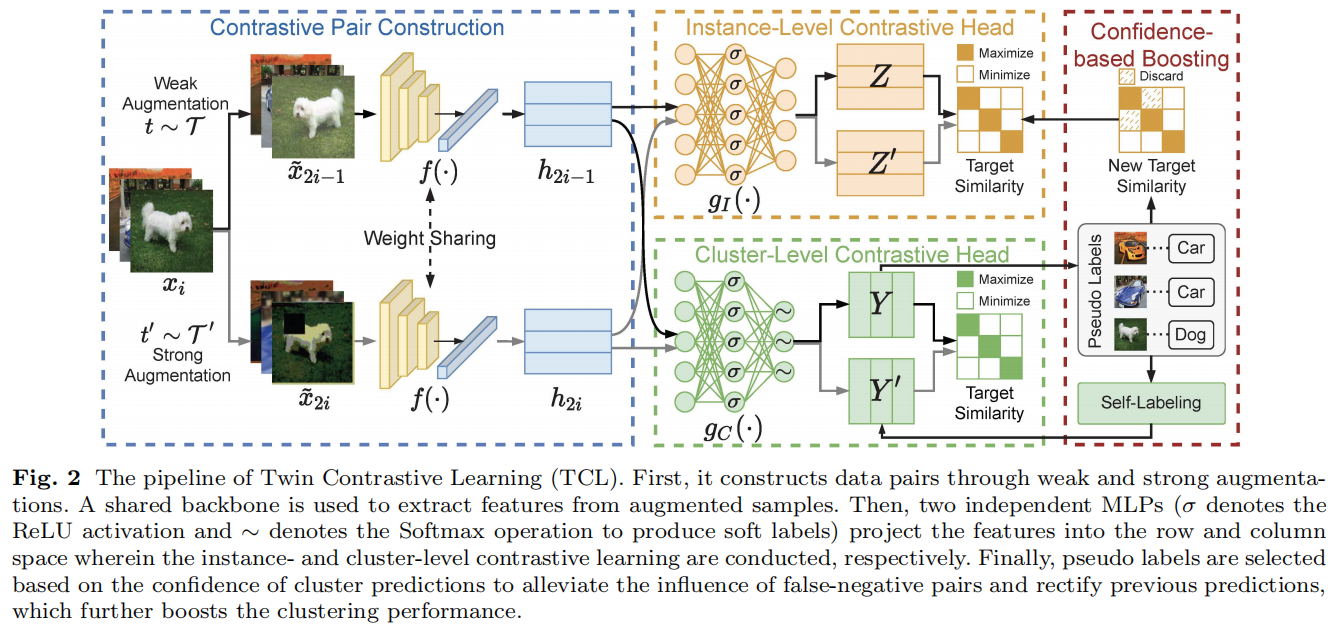
首先，它通过弱增强和强增强来构造数据对。一个共享的主干用于从增强的样本中提取特征。然后，两个独立的MLPs（σ表示ReLU激活，∼表示Softmax操作产生软标签）将特征投射到行和列空间，其中分别进行实例级和聚类级对比学习。最后，基于聚类预测的置信度选择伪标签，以减轻假阴性对的影响，并纠正之前的预测，进一步提高了聚类性能。

该模型由对比对构造（CPC）、实例级对比头（ICH）和集群级对比头（CCH）三个部分组成，通过双对比学习和基于信心的增强进行联合优化。具体来说，在双对比学习阶段，CPC首先通过数据增强来构造对比对，然后将对比对投射到一个潜在的特征空间中。然后，ICH和CCH通过最小化所提出的双对比损失，分别在特征矩阵的行空间和列空间进行实例级和聚类级对比学习。为了缓解对比学习中内在假阴性对的影响，并纠正聚类分配，我们提出了一种基于置信度的增强策略（CB）。详细地，选择了一些自信的预测作为伪标签，利用自监督对比损失和自标记损失对实例级和聚类级对比学习进行微调，进一步提高了聚类性能。
一旦模型收敛，CCH就可以对每个实例进行集群分配，以实现在线集群。值得注意的是，尽管双对比学习可以在我们的基本思想中直接在相同的对比头上进行，但我们通过实验发现，将其解耦成两个独立的子空间可以提高聚类性能（详细讨论见第4.6.4节）。
在本节中，我们首先介绍了CPC中对比对的构造，然后给出了训练中的双对比损失，最后详细阐述了我们基于信心的增强策略。

3.1对比对构造

受对比学习的最新发展的启发（Caron等人，2020；Chen等人，2020a），提出的TCL通过数据增强构建对比对。具体来说，对于每个实例xi，CPC随机抽样，并分别应用来自两个增强族t和t0的两组变换t和t0，得到两个相关样本（即数据对），表示为˜x2i−1=t（xi）和x˜2i=t0（xi）。

给定构建的对，使用共享主干f（·）通过h2i−1=f（˜x2i−1）和h2i=f（˜x2i）从增广样本中提取特征h。特定的骨干网用于处理不同类型的数据。在这项工作中，我们分别采用ResNet（He et al.，2016）和句子变压器（Reimers和Gurevych，2019）作为图像和文本数据的主干。

3.2双对比学习

在训练阶段，骨干、实例级对比头（ICH）和集群级对比头（CCH）根据以下双对比损失进行联合优化，即： \[\mathcal{L}_{t r a i n}=\mathcal{L}_{i n s}+\mathcal{L}_{c l u},\] 其中，\(\mathcal{L}_{i n s}\)为ICH上计算的实例级对比损失，\(\mathcal{L}_{c l u}\)为CCH上计算的簇级对比损失。
一般来说，可以添加一个动态权重参数来平衡整个训练过程中的两个损失，但显式地调整权重可能会违反无监督约束。在实践中，我们发现这两个对比损失的简单加法已经很有效了。

3.2.1实例级对比损失

实例级对比学习的目的是最大化正对的相似性，同时最小化负对的相似性。为了实现聚类，理想情况下，可以将类内实例定义为正，将类间实例定义为负。然而，由于没有给出先前的标签信息，我们基于数据扩充构建实例对作为一种折衷。具体地说，正对由来自同一实例的样本组成，负对组成则相反。
形式上，对于大小为N的小批，TCL对每个实例xi执行两种类型的数据增强，从而得到2N增强样本\(\left\{\tilde{x}_{1},\tilde{x}_{2},\cdot\cdot\cdot,\tilde{x}_{2i-1},\tilde{x}_{2i},\cdot\cdot\cdot,\tilde{x}_{2N}\right\}\)。每个样本˜x2i−1与其他样本形成2N−1对，其中我们选择相应的增广样本\(\{\tilde{x}_{2i-1},{\tilde{x}}_{2i}\}\)为正，并将其他2N−2对定义为负。
由于直接对特征矩阵进行对比学习可能会导致信息丢失（Chen et al.，2020a），我们叠加了一个两层非线性MLP gI（·），通过齐= gI（hi）将特征映射到子空间，其中应用实例级对比学习。成对相似性采用余弦距离进行测量，即， \[s(z_{i},z_{j})=\frac{\mathcal{z}_{i}\mathcal{z}_{j}}{\|z_{i}\|\|z_{j}\|},i,j\in[1,2N].\] 采用InfoNCE损失（Oord等人，2018）来优化等式定义2的成对相似性，在不丧失一般性的情况下，将给定的增广样本˜xi（假设它与˜xj形成一个正对）的损失定义为 \[\ell_{i}=-\log\frac{\exp(s(z_{i},z_{j})/\tau_{I})}{\sum_{k=1}^{2N}\mathrm{~l}_{[k\neq i]}\exp{(s(z_{i},z_{k})/\tau_{I})}},\] 其中，τI是控制柔软度的实例级温度参数，而1[k=i]是一个计算当为1k/=i时的指标函数。为了识别每个增广样本的正对应物，需要计算所有增广样本的实例提升对比损失，即： \[\ell_{i n s}={\frac{1}{2N}}\sum_{k=1}^{2N}\ell_{k}.\] 3.2.2集群级对比损失

当一个样本被投影到一个维数等于聚类数的子空间时，其特征的第i个元素表示其属于第i个聚类的概率。换句话说，特征向量对应于其聚类分配概率。
假设目标簇数为M，类似于实例级对比头，我们使用另一个双层MLP gC（·）通过yi = gC（hi）将特征投影到一维空间中。这里的yi对应于增强样本˜xi的聚类分配概率。形式上，让\(Y=[y_{1},\cdot\cdot\cdot,y_{2i-1},\cdot\cdot\cdot,y_{2N-1}]\in {\mathcal{R}}^{N\times M}\)是弱增强T下的簇分配概率（和\(Y^{\prime}=\left[y_{2},\cdot\cdot\cdot,y_{2i},\cdot\cdot\cdot,y_{2N}\right]\)强增强T0下的y2N）。根据图1所示的观察结果，Y和Y0的列对应于小批处理上的聚类分布，可以解释为特殊的聚类表示。我们想指出的是，即使维度大于地面真实的星团数，这一观测结果仍然成立。在这种情况下，考虑了一个更细粒度的集群结构，并在Barlow Twins中验证了其有效性（Zbontar et al.，2021）。
为了清晰起见，我们将Y的i-列表示为ˆy2i−1（对Y0的i-列表示为ˆy2i），即在弱（和强）数据增强下的簇i的表示。同一簇在两个增强下的表示形成正簇对{yˆ2i−1，yˆ2i}，i∈[1，M]，而其他对被定义为负。同样，我们使用余弦距离来度量簇ˆyi和簇ˆyj之间的相似性，即 \[s(\hat{y}_{i},\hat{y}_{j})=\frac{\hat{y}_{i}^{\top}\hat{y}_{j}}{\|\hat{y}_{i}\|\|\hat{y}_{j}\|},i,j\in[1,2M]\] 在不丧失一般性的情况下，采用以下损失函数从除其对应的ˆyj外的所有其他2M−2集群中识别集群ˆyi，即： \[\hat{\ell}_{i}=-\log\frac{\exp(s(\hat{y}_{i},\hat{y}_{j})/\tau_{C})}{\sum_{k=1}^{2M}\mathrm{l}_{[k\mp i]}\exp\left(s(\hat{y}_{i},\hat{y}_{k})/\tau_{C}\right)},\] 其中，τC是控制柔软度的簇级温度参数，而1[k=i]是一个评价为1 iff k = i的指标函数。通过遍历所有的簇，可以计算出簇级的对比损失 \[\mathcal{L}_{c l u}^{\prime}=\frac{1}{2M}\sum_{k=1}^{M}\hat{\ell}_{k}.\] 由于简单地优化上述聚类级对比损失可能会导致简单的解决方案，即大多数样本被分配到几个聚类中，我们添加了一个聚类熵，以防止模型崩溃，并实现更平衡的聚类（Ghasedi Dizaji等人，2017；Huang等人，2020）。公式上，让\(P(\hat{y}_{2i-1})\ ={\frac{1}{N}}\sum_{k=1}^{N}Y_{k i}\)成为弱增强条件下簇i在一个小批内的分配概率，\(P(\hat{y}_{2i})\ ={\frac{1}{N}}\sum_{k=1}^{N}Y^{\prime}_{k i}\)成为强增强条件下簇i在一个小批内的分配概率，然后计算出团簇熵 \[{ H}_{c l u}=-\sum_{i=1}^{2M}[{\cal P}(\hat{y_{i}})\log{\cal P}(\hat{y_{i}})].\] 综上所述，簇级对比损失最终定义为 \[\mathcal{L}_{c l u}=\frac{1}{2M}\sum_{k=1}^{2M}\hat{\ell}_{k}-H_{c l u}.\] 3.3基于置信度的提升

随着训练的进行，我们注意到该模型倾向于做出更自信的预测（即，聚类分配概率接近于一个热点）。这些相反的预测更有可能是正确的（见图4）。基于这一观察结果，在推进阶段，我们逐步选择最自信的预测作为伪标签，以微调实例级和集群级的对比学习。