Learnable Subspace Clustering

Learnable Subspace Clustering

摘要

​  本文研究了具有数百万个数据点的大规模子空间聚类（\(LS^2C\)）问题。许多流行的子空间聚类方法都不能直接处理\(LS^2C\)问题，尽管它们被认为是针对小规模数据点的最新方法。一个简单的原因是，这些方法经常选择所有的数据点作为一个大型的字典来构建巨大的编码模型，这导致了较高的时间和空间复杂度。在本文中，我们开发了一个可学习的子空间聚类范式来有效地解决LS2C问题。关键的概念是学习一个参数函数来将高维子空间划分为它们的底层低维子空间，而不是需要计算要求的经典编码模型。此外，我们提出了一个统一的、鲁棒的、预测编码机（RPCM，robust predictive coding machine）来学习参数函数，它可以通过交替最小化算法来求解。此外，我们还给出了参数函数的有界收缩分析。

1.介绍

​  高维大数据集越来越多无处不在，在计算机视觉和机器学习任务中越来越可用和流行。例如，[1]和YouTube上分别有数百万帧的图像和数十亿帧的视频。不幸的是，大数据的高维性通常会导致算法的高时间和空间复杂性，而大数据中的复杂错误（如噪声、异常值和损坏）严重损害了它们的性能[3]。然而，高维大数据通常是由低维子结构[4]组成的。因此，在大数据中寻找低维结构是降低时间和空间复杂度、减少复杂误差的影响、提高学习和分割任务性能的一种可能的解决方案。
​  子空间聚类[5]是最常见的鲁棒地恢复高维数据低维表示的方法之一，因为它已经提供了理论保证[6]，[7]成功应用于众多研究领域，如图像分割[8]，[9]，人体运动分割[10]，图像处理[11]，[12]，顺序数据聚类[13]，医学成像[14]和生物信息学[15]。特别是光谱式方法（如稀疏子空间聚类（SSC）[16]、低秩表示（LRR）[17]、[18]和最小二乘回归（LSR）[19]）近年来由于在小规模数据集（如霍普金斯155[20]和扩展YaleB [21]）上的良好性能好而受到越来越多的关注。
​  然而，经典的范式限制了子空间聚类方法来处理高维大数据（例如，数以百万计的图像[23]和视频[2]）。一个简单的原因是，SE属性导致了一个大的自我表达字典和巨大的简约编码模型。它们导致了计算瓶颈，因为它们通常通过迭代许多优化算子来解决，如收缩阈值算子[24]和奇异值分解（SVD）[25]。因此，它很自然地产生了一个具有数百万个数据点的具有挑战性的子空间聚类问题。
​  为了解决这个问题，我们开发了一个可学习的子空间聚类（LeaSC）范式（见图1），以快速和稳健地从高维大数据中恢复低维结构。

image-20250216110434525

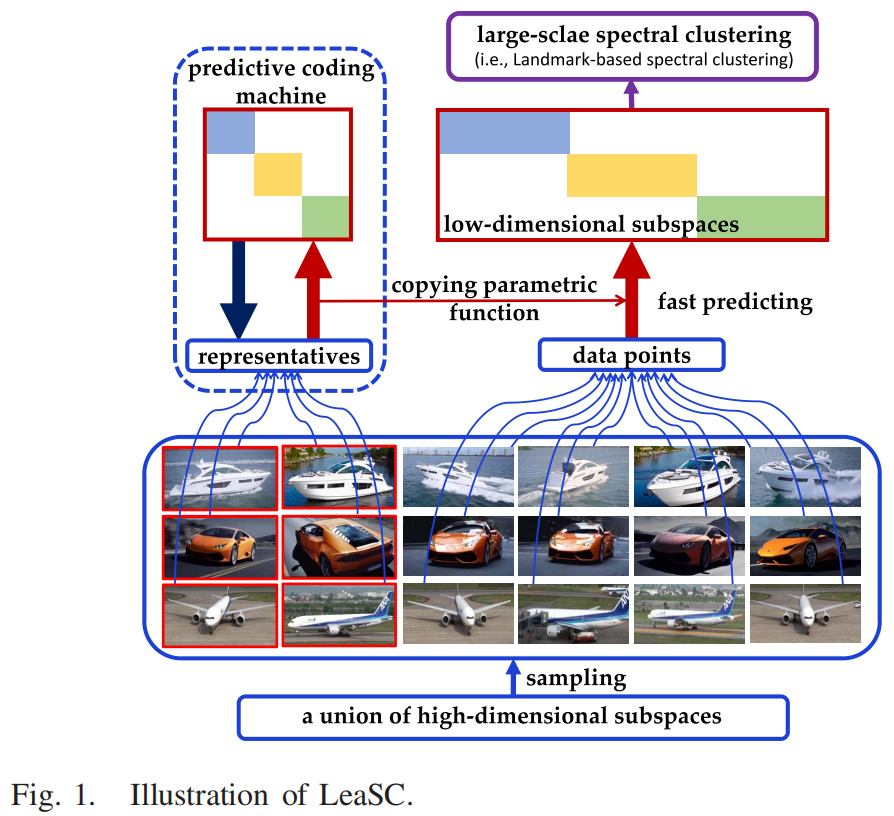
​  首先，给定一组大的高维数据点，通常来自高维子空间[16]，[17]，我们发现一些代表或样本，可以有效地描述绘制数据点[26]有效地减少大自我表达的字典的大小。其次，利用代表来学习从高维子空间到低维子空间的参数函数（例如，神经网络）。第三，其余的数据点通过学习到的参数函数而不是简约的编码模型快速映射到低维编码中。最后，我们采用基于地标的光谱聚类（LbSC）[27]对代码进行聚类。
​  在已开发的LeaSC范式中，我们提出了一种新的模型，称为预测编码机（PCM）来学习参数函数。通过找到代表作为一个小的自我表达的字典，PCM的基本过程是优化理想回归，稀疏，低秩，或弹性网络代码通过使用一个平方的弗罗比尼乌斯范数，1规范，核范数或弹性网正则化，并共同训练参数函数近似理想的代码。此外，由于在现实应用[16]，[17]中由于测量/处理噪声经常被噪声（如高斯噪声、稀疏异常项和缺失项）破坏，我们通过考虑各种噪声污染的数据，将PCM扩展到鲁棒PCM（RPCM）。由于参数函数的非线性，RPCM是非凸的。我们提出了一种拟凸优化方法来解决它们，该方法替代了交替方向的乘子法（ADMM）[28]，[29]和梯度下降法（GD）算法[30]，[31]。通过选择适当数量的代表，给出了保证参数函数能够正确地将高维数据点压缩到代表的理想码的理论条件。这进一步验证了在代表上训练的PCM和RPCM可以有效地执行具有数百万个数据点的子空间聚类。总的来说，我们的主要贡献如下。

• 我们开发了一个有效的范式，称为LeaSC，以一种高效的方式处理具有数百万个数据点的子空间聚类问题。我们的目标是学习参数函数，将高维子空间划分为它们的底层低维子空间，而不是经典编码（CCod）模型的昂贵代价。这个参数函数导致了LeaSC的线性复杂性。
• 我们提出了一个PCM模型及其鲁棒扩展RPCM来学习LeaSC范式中的参数函数。由于RPCM是非凸的，我们提出了一种拟凸的优化方法，通过交替的ADMM和GD来求解它。
• 我们提供了由PCM模型学习到的参数函数的有界收缩分析。结果表明，与原始子空间聚类模型相比，参数函数能很好地计算高维数据的收缩低维表示。

​  本文是对我们之前几个会议作品[32]-[35]的重要扩展。与会议版本相比，有四个主要的区别。首先，我们开发了一个统一的LeaSC范式来集群数百万个数据点。其次，我们提出了一个具有弗罗比尼乌斯范数[32]、核范数[33]、1-范数或弹性网正则化的平方的一般RPCM。第三，我们给出了一个保证学习到的参数函数收缩的理论条件。第四，我们在百万尺度的数据集（即MNIST8M [23]和YouTube8M [2]）上添加了更多的实验，以证明LeaSC的有效性。
​  本文的其余部分组织如下。我们在第二节中回顾了相关的子空间聚类工作。我们统一的LeaSC范式和RPCM在第三节中开发。我们在第四节中提出了一种针对RPCM的拟凸优化方法。我们在第五节中提供了一个收缩子空间恢复理论，第六节显示了实验结果。最后，在第七节中得出了结论。

2.相关工作

​  在本节中，我们主要回顾了CCod模型、大尺度光谱聚类（LsSPC）方法和可伸缩的编码方法，因为它们在小规模数据集上显示出了良好的性能。此外，我们还讨论了直接编码模型来应用我们的LeaSC范式。

A. CCod模型

​  一般来说，CCod模型基于SE属性[16]，采用不同的编码模型来计算相似矩阵，并将（大规模）光谱聚类[22]，[36]-[38]应用于该相似矩阵。例如，SSC [16]、LRR [17]和LSR [19]分别使用1、核范数和2正则化的编码模型构建相似度矩阵。根据SE属性，这些编码模型及其变体[18]，[39]-[41]通常选择所有的数据点作为字典。当面对大数据集（例如，数百万张图像）时，字典中的自动（或基础）的数量非常大。在实践中，这个大型字典将导致用于谱聚类的高维（百万）相似矩阵，并进一步导致如果资源有限，编码模型无法在一台机器上运行。此外，由于采用迭代优化方式[42]、[43]进行求解，因此它们仍然存在较高的时间复杂度。因此，简约的编码模型需要高的计算时间和大量的内存来构建相似矩阵。此外，分布式LRR（DLRR）[44]和分散SSC（DSSC）[45]将一个大数据集划分为许多小数据集，并使用LRR或稀疏编码来计算LRR或稀疏表示。然而，它们仍然需要大量的计算机资源。幸运的是，我们探索了LeaSC范式来学习一个参数函数，以快速计算相似度矩阵的表示。

B. LsSPC

​  一般的谱聚类方法[22]需要计算由相似矩阵组成的归一化拉普拉斯矩阵的特征向量，并应用K-均值对特征向量进行聚类。不幸的是，计算特征向量是非常昂贵的[27]。因此，它导致了处理大规模数据集的难题。因此，将光谱聚类方法扩展到LsSpC中，通过以下两种方式对大数据进行聚类。首先，利用¨值方法逼近特征向量[46]，以降低计算代价，在许多子系统[47]中特征值计算是并行的。其次，选取少量样本作为地标点，构建K-means [48]、样本外[49]和随机选择[27]的稀疏相似矩阵。它们将导致较差的聚类结果，因为一个不可分割的相似度矩阵通常是由具有复杂结构的原始数据构建的。通过比较，我们可以通过在已开发的LeaSC范式中使用我们的RPCM模型来学习鲁棒表示。

C. 可扩展编码方法

​  在以下两种策略中，还提出了可扩展的编码方法来进行大数据的聚类。首先，可伸缩的SSC [50]，[51]是用一个小的子字典来解决一系列的子问题，以减少计算时间。其次，采样-聚类分类（S-C-C）[42]，[43]从大数据集中选择一个小的子数据集，使用SSC、LRR和LSR进行子空间聚类，并学习一个简单的线性分类器或基于协作表示的分类器（CRC）[52]，获得最终的聚类结果。不幸的是，可扩展SSC仍然需要更多的计算时间，例如，它花费1000秒处理10万个数据样本[50]，S-C-C将导致较差的聚类结果，因为简单的分类器在复杂样本[53]中不容易识别。通过比较，我们可以快速计算鲁棒表示来构造相似度矩阵，并执行LsSpC（如LbSC [27]）。

D. 直接编码模型

​  在我们的LeaSC范式中，我们提出了RPCM模型来学习参数函数，以直接编码数据点的表示，以降低计算复杂度。实际上，有一些直接编码模型，如自动编码器（AEs）[54]、稀疏自动编码器（SAEs）[55]、[56]、去噪自动编码器（DAEs）[57]、预测稀疏分解（PSD）[34]、[58]、鲁棒主成分分析编码器（RPCAec）[59]和潜在LRR（latLRR）[60]。AE和SAE都不是健壮的模型，需要干净的输入数据。虽然DAE和PSD可以学习健壮的代码，但它仍然需要干净的输入数据。不幸的是，真实的数据通常会有大量的噪声[16]，[17]。为了处理噪声，RPCAec [59]和latLRR [60]可以通过分离噪声快速计算出鲁棒的低秩码。然而，RPCAec [59]只处理一个单个低秩子空间，而latLRR [60]只学习一个线性预测器，这很难捕获复杂的数据结构[31]，[53]。相比之下，我们的RPCM不需要明确的数据，也不需要一个非线性预测器来计算鲁棒表示。更重要的是，我们还将把这些编码模型应用到LeaSC范式中来处理LS2C。

3. LEASC

​  在本节中，我们开发了一个有效的LeaSC范式来聚集大量的多子空间数据点。具体地说，我们首先介绍了一个用于子空间聚类的机器学习问题。为了解决这一问题，我们提出了一个统一的PCM方法，即从高维空间到低维空间学习一个参数函数。然后利用参数函数快速恢复数据点的子空间表示。最后，我们对子空间表示进行LbSC [27]，以获得最终的聚类结果。

​  标记法：\(\mathcal{X}\)记为高维空间。随机变量、普通向量、矩阵和矩阵块分别用大写、小写、大写和黑板粗体写，例如，X、x、\(\mathbf{X}\)和\(\mathbb{X}=\binom{\mathbf X}{\mathbf Y}\)。期望（离散情况，p为概率质量）用\(\operatorname{E}_{p(X)}({\mathcal{L}}(X))\ \ =\ \sum_{\mathbf{x}}p(X\ \ =\ \mathbf{x}){\mathcal{L}}({\mathbf{x}})\)表示。给定数组\(\mathbf{A}=\,[a_{i\,j}\,]\,\in\,\mathbb{R}^{d\times n}\)，我们的核范数用\(\|\mathbf{A}\|_{*}=\textstyle\sum_{i}\sigma_{i}(\mathbf{A})\)（A的奇异值之和）表示，\(\ell_{2,1}\)用\(||\mathbf{A}||_{2,1}=\sum_{j}||\mathbf{a}_{:j}||_{2}\)表示，F范数用\(||\mathbf{A}||_{\mathrm}=(\sum_{i j}(a_{i j})^{2})^{1/2}\)表示和f范数的平方用\(||\mathbf{A}||_{\mathrm{F}}^{2}=\sum_{i j}(a_{i j})^{2}\)表示。一个包含m个元素的集合的n-组合数用\(\binom{m}{n}\)表示。

A.问题陈述

​  在本节中，我们描述了一个用于子空间聚类的显式机器学习问题。具体地说，我们考虑一个d维高维空间\(\mathcal{X}\)，它是s≥1个未知低维\(d_{i}=\dim(\mathcal{X}_{i})(0\lt d_{i}\lt d,i=1,\ldots,s)\)的线性或仿射子空间\(\{\mathcal{X}_{i}\}_{i=1}^{s}\)的未知并集。形式上，我们假设\(X\in\mathcal{X}\)是一个根据未知分布p (X)的随机变量，它可以分解为 \[X=\mathbf{B}Z=[\mathbf{B}_{1}\quad\cdots\quad\mathbf{B}_{k}]{\left[\begin{array}{l}{Z_{1}}\\ {\cdots}\\ {Z_{k}}\end{array}\right]}\] ​  其中，\(\mathbf{B}_{i}\in\mathbb{R}^{d\times d_{i}}\)是一个线性跨越第i个数据子空间的未知子空间基，\(Z_i\)是一个\(d_i\)维低维子空间表示变量。我们的子空间聚类问题的机器学习目标是寻找一个参数函数\(f(\bullet;\theta)\)，它从X预测Z，以将空间X划分为子空间\(\{\mathcal{X}_{i}\}_{i=1}^{s}\)。
​  为了实现这一目标，根据基础分布p (X)，将f的预期风险定义为 \[\operatorname*{min}_{\theta}\ E_{p(X)}[\mathcal{L}(Z,f(X;\theta))]\quad\mathrm{s.t.}\ X=\mathrm{B}Z\] ​  其中，\(\mathcal{L}(Z,f(X;\theta))\)是Z和\(f(X;\theta)\)之间的损失函数，例如，平方误差损失函数\((Z-f(X;\theta))^2\)。由于p (X)未知，预期风险不能在(2)中直接测量。但是我们可以考虑一个由N个数据点\(\mathbf{X}=[\mathbf{x}_{i}]_{i=1}^{n}\in\mathbb{R}^{d\times n}\)构成，且假设为p(x)分布的经验分布\(p^0(X)\)。相应的在p0(X)上的经验风险1平均值可以描述为 \[\operatorname*{min}_{\theta}\ E_{p^0(X)}[\mathcal{L}(Z,f(X;\theta))]\quad\mathrm{s.t.}\ X=\mathrm{B}Z\] ​  在学习参数函数\(f(\bullet;\theta)\)后，将空间X快速映射到低维表示空间，很容易划分为子空间\(\{\mathcal{X}_{i}\}_{i=1}^{s}\)。我们将在第三节-b节中提出一个稳健和有效的模型，以更好地计算经验风险。
​  备注1：我们的机器学习问题不同于传统的子空间聚类问题[5]。后者通常考虑通过使用昂贵的稀疏/低秩优化从空间X中得到的给定（训练）数据点X的分割。前者学习一个参数函数，将空间X划分为子空间\(\{\mathcal{X}_{i}\}_{i=1}^{s}\)。它的过程是从空间X中提取一个数据集，或从给定的X中选择一个小的数据集，并训练参数函数。这个过程有一个明显的好处，即参数函数可以快速地将新的（大的）数据点投影到低维表示中，并分组到它们的子空间中。