Mesoscopic Insights:Orchestrating Multi-Scale & Hybrid Architecture for Image Manipulation Localization
Mesoscopic Insights: Orchestrating Multi-Scale & Hybrid Architecture for Image Manipulation Localization
Xuekang Zhu1,2,Xiaochen Ma1,2, Lei Su1,2,Zhuohang Jiang3,Bo Du1,2,Xiwen Wang1,2,Zeyu Lei1,2,Wentao Feng1,2,Chi-Man Pun4,Ji-Zhe Zhou1,2†
1计算机学院,四川大学
2机器学习与产业智能工程研究中心,中国教育部
3香港理工大学
4澳门大学科技学院计算机与资讯科学系
摘要
介观层面作为宏观与微观世界的桥梁,填补了两者长期忽视的空白。图像操控定位(IML)作为从虚假图像中探寻真相的关键技术,长期以来依赖于微观层面的痕迹信息。然而在实际应用中,大多数篡改行为旨在通过改变图像语义来欺骗观众。因此,图像操控通常发生在物体层面(宏观层面),这与微观痕迹同样重要。将这两个层面整合到介观层面,为IML研究提供了全新视角。受此启发,本文探索如何同时构建IML所需的微观与宏观信息介观表征,并提出Mesorch架构来协调二者。具体而言,该架构具有两大核心特点:首先,它将Transformer与CNN进行并行融合——Transformer负责提取宏观信息,CNN则捕捉微观细节;其次,它能在不同尺度间灵活切换,实现微观与宏观信息的无缝衔接。基于介观表示架构,本文还提出了两种基线模型,专门用于解决中观表示任务。通过在四个数据集上的大量实验验证,我们的模型在性能表现、计算复杂度和鲁棒性方面均超越了现有最优方案。
代码—https://github.com/scu-zjz/Mesorch
扩展版本—https://arxiv.org/abs/2412.13753
1.引言
介观系统存在于宏观与微观尺度之间。介观尺度的物体足够大,能够表现出宏观特性,同时又展现出与量子力学相位相关的干涉现象,这与微观系统相似。这种双重性正是它被称为“介观”的原因——Yoseph lmry.

图1:三种篡改类型中的伪影示例。第三列中的红色虚线框表示第四列中放大区域的范围。第四列中的红色箭头指向被认为是篡改痕迹的伪影。
多媒体篡改技术的快速发展使得检测和定位图像篡改更加具有挑战性。伪造逼真的图像变得容易,助长了篡改事件和错误信息,突显出需要有效的取证方法。如图1所示,在图像篡改领域,现有技术主要分为三大类(Pun, Yuan, and Bi 2015; Bi, Pun, and Yuan 2016;Wu et al. 2019; Verdoliva 2020; Wei et al. 2023):拼接(将不同图像片段组合生成新图)、复制移动(在同幅图像内复制粘贴区域)以及修复(移除瑕疵后用合理内容填补)。尽管复杂的手工篡改可能逃过人眼察觉,但每种操作在微观层面仍会留下可辨识痕迹。因此,当前图像篡改定位(IML)技术普遍将微观特征提取视为关键任务——通过捕捉图像RGB噪声(Zhou et al. 2018; Bayar and Stamm 2018)、边缘信号(Zhou et al. 2020; Chen et al. 2021)或高频特征(Li and Huang 2019; Wang et al. 2022a)等微观特征来识别篡改痕迹。这些微观特征在揭示瑕疵和定位篡改区域方面通常效果显著。

图2:CASIAv2数据集的随机样本。红色线条标出了篡改区域的清晰边界。第一列显示与物体完全无关的篡改行为,其余四列则展示了与物体相关的篡改行为。
然而,如图2所示,大多数篡改行为通常通过改变或模糊图像语义来欺骗观众。例如,在CASIAv2数据集中,约80%的样本涉及物体操控。此外,物体是否被篡改的可能性会根据其对整体图像语义的贡献度而变化——比如前景中的人类和动物比背景中的树木山峦更容易被篡改。因此我们认为,理解物体层面(宏观层面)的语义特征对于识别篡改区域和划定可疑范围至关重要。不过仅凭宏观层面的语义特征还不足以生成篡改掩膜,因为缺乏必要的细节来检测复杂的伪影。
因此,探索将微观与宏观信息整合至介观层面的路径,可能成为提升中介模型(IML)研究的新突破口。DiffForensics(Yu
et
al.2024)指出,伪影存在于介观层面——即介于微观与宏观之间的中间层级,兼具两者的特征。但该研究未深入探讨如何从技术层面刻画这一层级。基于我们前期的深度分析,我们提出通过同步捕捉微观特征与提取宏观语义来定义介观层面的伪影捕获,这为中介模型任务提供了新范式。基于此范式,我们创新性地提出了Mesorch(介观编排,Mesoscopic-Orchestration)架构,该架构采用专门设计的并行编码器和解码器结构来表征介观层面,从而实现两个层级间的高效协调,更精准地捕捉介观层面的伪影特征。
在编码器阶段,当前研究(Huang
et al. 2016;Zhang et al. 2018; Yuan et al.
2021)表明,卷积神经网络(CNN)和Transformer模型分别擅长处理微观特征与宏观语义。然而,现有大多数图像微解构方法(Wu
et al. 2019; Hu et al. 2020;Guillaro et al.
2023)仍完全依赖单一架构进行决策。尽管部分模型如ObjectFormer(Wang et al.
2022a),已认识到CNN与Transformer结合的优势,但其设计仍采用线性连接的顺序架构。这种顺序架构常导致单一模型占据主导地位——由于大部分计算资源或参数集中在该模型上,反而弱化了另一模型的优势。因此,其性能无法超越单架构模型,也未能充分融合微观与宏观层面的优势。为解决这一局限,我们采用并行架构同时运用CNN和Transformer。这种设计有效整合了两种方法的优势,特别针对介观层面的伪影捕捉问题。
在此基础上,浅层特征图提供微观特征,而深层特征图则呈现宏观语义。因此,在解码阶段采用多尺度方法同步解码不同尺度的特征图,有助于模型更精准捕捉介观层面的伪影特征。类似地,诸如MVSS-Net(Chen
et al. 2021)和Trufor(Guillaro et al.
2023)等现有模型,在此阶段也采用了多尺度解码方法。然而,这些模型假设所有尺度的权重相等且未进行显式调整,可能导致忽略尺度间的差异。这既可能造成关键特征利用率不足,也可能过度强调次要特征,从而影响整体性能。为有效解决这一问题,我们引入自适应权重模块,动态调整各尺度的重要性。此外,通过剪枝非关键尺度,模型在保持性能的同时显著降低计算成本和参数量。
综上所述,我们提出了一种名为Mesorch的混合模型架构,该架构融合了卷积神经网络(CNN)和Transformer模型,通过动态调整尺度权重来高效表征介观层级。通过剪枝低重要性尺度,我们有效降低了参数量和计算成本,最终构建出两个基准模型。在四个数据集上的测试表明,该模型在F1分数、鲁棒性和运算量(FLOPs)方面均达到业界领先水平。
我们的贡献有三个方面;
- 我们提出Mesorch架构,这是一种融合卷积神经网络与Transformer模型优势的混合架构。该架构采用多尺度协同机制,有效整合微观与宏观层面的信息,从而精准捕捉图像医学学习任务中的介观特征。
- 我们提出了一种自适应加权模块,能够动态调整每个尺度的重要性。此外,通过选择性地剪枝影响较小的尺度,我们的方法在保持鲁棒性和性能的同时,显著降低了计算成本和参数量。
- 我们基于Mesorch架构开发了两个基准模型。在基准数据集上的全面实验表明,我们的方法在F1分数、鲁棒性和浮点运算量方面达到了业界领先水平。
2.相关工作
2.1.篡改定位的体系结构
基于CNN的模型
在图像篡改检测领域,基于卷积神经网络(CNN)的模型凭借其强大的特征提取能力长期占据主流地位,尤其擅长捕捉表明图像被篡改的局部纹理异常。诸如ManTra-Net
(Wu et al.2019)和SPAN (Hu et al. 2020)等代表性方案,通过采用VGG
(Simonyan and Zisserman 2015)和ResNet-50 (He et al.
2016)等架构,有效捕捉局部纹理异常特征。近年来,研究者们开始整合对比学习技术,例如NCL
(Zhou et al.2023),进一步提升了检测系统的定位能力。
基于Transformer的模型
基于对更广泛上下文理解的需求,Transformer架构的IML-ViT
(Ma et al. 2023)率先将该架构引入IML领域,而TruFor (Guillaro et al.
2023)则采用了SegFormer (Xie et al.
2021)。这些模型擅长综合多维度上下文信息,通过动态聚焦潜在操作区域来提升定位精度,标志着该领域的重大突破。类似地,MGQFormer
(Zeng et al.
2024)采用基于查询的Transformer架构来精确定位操作区域。通过聚焦上下文相关特征,该模型显著提升了操作定位精度,充分展现了Transformer技术在提供稳健、上下文感知解决方案方面的强大优势,超越了以往方法。
基于混合CNN-Transformer模型
除了上述模型之外,像ObjectFormer
(Wang et al.
2022a)这类将卷积神经网络与transformer进行序列式结合的混合方法也备受关注。ObjectFormer采用EfficientNet架构作为编码器的初始部分,将输入数据下采样为特定特征块,随后这些特征块依次输入到双流视觉transformer中。
2.2.多尺度应用
在图像处理与定位领域,多尺度技术已成为提升不同分辨率下特征分析效果的重要手段。以MVSSNet (Chen et al. 2021)为例,该模型采用多视角、多尺度的监督策略来检测图像篡改行为。通过整合局部边缘信息与全局上下文特征,MVSSNet运用多尺度特征学习技术精准识别篡改区域,展现出在各类数据集和场景中高度泛化的解决方案。类似地,TruFor (Guillaro et al. 2023)基于SegFormer (Xie et al. 2021)主干网络,有效整合了整幅图像的空间关联性。其多尺度方法通过结合细粒度局部特征与广义上下文信息,显著提升了篡改异常的定位精度,确保了操作痕迹的精准识别与鲁棒性。
3.方法
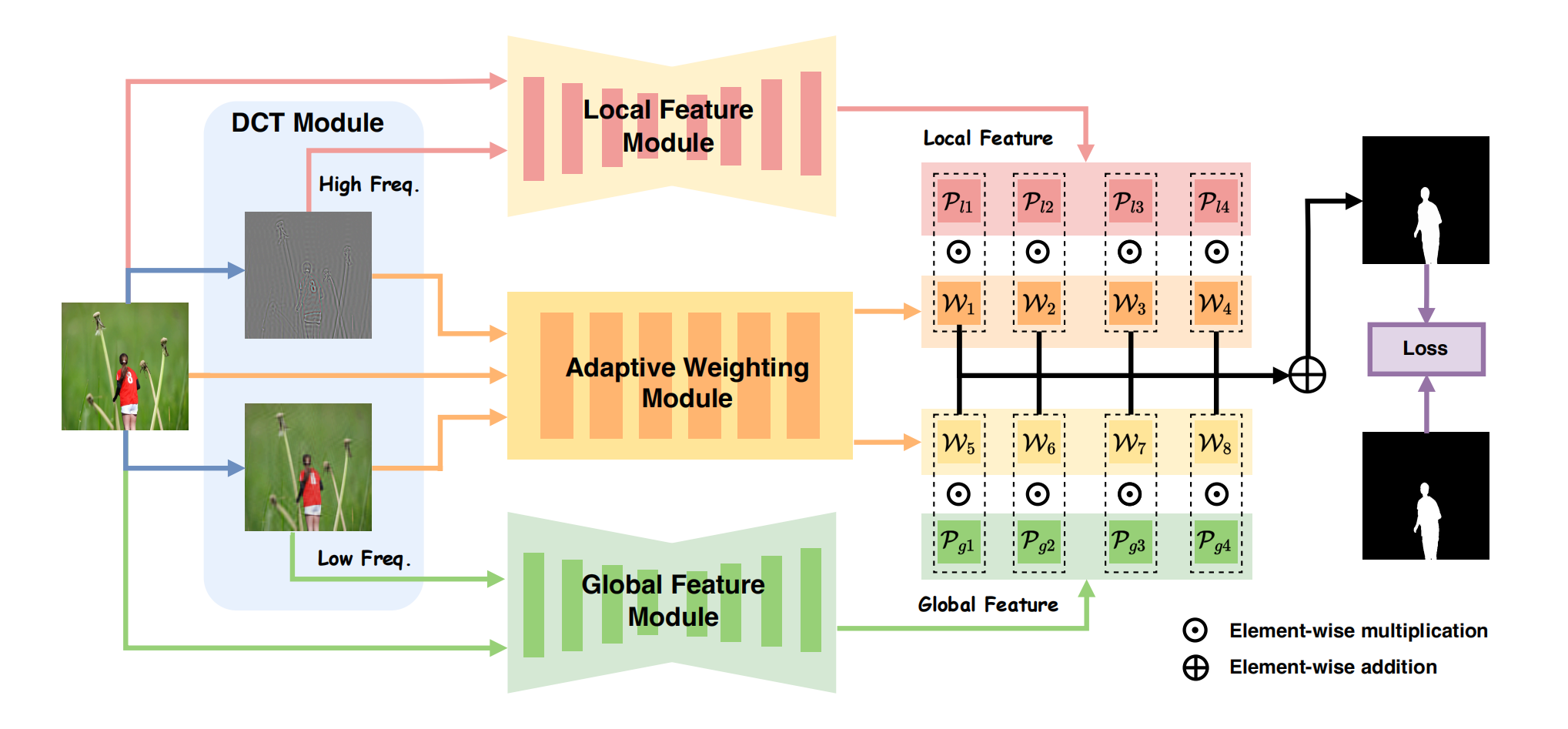
图3:Mesorch框架示意图:输入的RGB图像首先在DCT模块中进行高频与低频处理,分别生成对应的高频和低频表征。局部特征模块通过结合原始图像与高频图像,专注于检测细粒度操作;全局特征模块则利用原始图像与低频图像捕捉物体级别的篡改线索。自适应加权模块通过为局部特征和全局特征分配像素级权重,动态整合这些图像信息。最终生成的组合特征用于预测任务,并与真实标签对比计算损失值。
在本节中,我们介绍了如图3所示的Mesorch框架。该流程始于RGB图像,通过离散余弦变换(DCT)提取高频与低频特征(Gonzalez and Woods 2018)。随后将这些特征与原始图像融合,生成高频增强图像和低频增强图像。高频增强图像被传递至局部特征模块,而低频增强图像则进入全局特征模块。两个模块分别输出四个不同尺度的特征图,对应的解码器处理这些特征图以生成操作区域的初始预测结果。通过加权融合这些多尺度预测结果,最终生成综合预测。为提高效率,在模型初步收敛后采用剪枝方法,通过剔除次要特征尺度来优化参数数量和运算量。
3.1 整合局部和全局信息以增强预测
隐藏在介观层面的特征可能在RGB域中并不显著,但可以通过频域信息进行放大(Wang et al. 2022a)。因此,我们从频域中提取高频和低频特征,以增强局部和全局特征编码器模块的能力。
3.1.1 采用离散余弦变换增强功能
最初,如图3所示,对尺寸为H×W×3的RGB图像x进行离散余弦变换(DCT)处理,将其分解为高频分量\({\bf x}_{h}\)和低频分量\({\bf x}_{l}\)。这些分量保留了H×W×3的维度后,与原始图像x结合,形成增强表示以供后续处理: \[{\bf I}_{h}=\{\bf x,{\bf x}_{h}\},~~~{\bf I}_{h}\in\mathbb{R}^{H\times W\times6}\]
\[{\bf I}_{l}=\{\bf x,{\bf x}_{l}\},~~~{\bf I}_{l}\in\mathbb{R}^{H\times W\times6}\]
3.1.2 特征编码和尺度解码
在进一步增强高频和低频特征后,高频增强图像\({\bf I}_{h}\)由局部特征编码器处理,而低频增强图像\({\bf I}_{l}\)由全局特征编码器处理。每个编码器随后输出四个不同尺度的特征: \[\begin{matrix}\{L_{s_{1}},L_{s_{2}},L_{s_{3}},L_{s_{4}}\}=\mathrm{LocalFeatureEncoder}({\bf I}_{h}),\\L_{s_{i}}\in\mathbb{R}^{\frac{H}{2^{(i+1)}}\times\frac{W}{2^{(i+1)}}\times{C}_{i_{local}}}\end{matrix}\]
\[\begin{matrix}\{G_{s_{1}},G_{s_{2}},G_{s_{3}},G_{s_{4}}\}=\mathrm{GlobalFeatureEncoder}({\bf I}_{l}),\\G_{s_{i}}\in\mathbb{R}^{\frac{H}{2^{(i+1)}}\times\frac{W}{2^{(i+1)}}\times{C}_{i_{global}}}\end{matrix}\]
这里,\({C}_{i_{local}}\)和\({C}_{i_{global}}\)分别表示局部编码器和全局编码器在每个尺度i上的输出通道总数。
由局部和全局特征编码器在尺度i
=
1、2、3、4生成的特征图随后通过解码器处理,解码器为每个尺度i输出形状为\(\frac{H}{4}\times\frac{W}{4}\times1\)的预测掩膜:
\[P_{l_{i}}=\mathrm{LocalFeatureDecoder}(L_{s_{i}})\]
\[P_{g_{i}}={\mathrm{GlobalFeatureDecoder}}(G_{s_{i}})\]
将局部预测和全局预测相结合,生成形状为\(\frac{H}{4}\times\frac{W}{4}\times1\)的总和最终预测掩膜。然后将该掩膜调整为图像的原始尺寸(H×W),生成最终预测掩膜\(P_{\mathrm{final}}\): \[P_{\mathrm{final}}=\mathrm{Resize}\left(\sum_{i=1}^{4}(P_{l_{i}}+P_{g_{i}}),H,W\right)\] 模型性能的评估通过计算\(P_{\mathrm{final}}\)与真实掩模之间的交叉熵损失来实现,其中真实掩模用于标识图像中实际被篡改的区域。该真实掩模作为二值化图层突出显示被篡改区域,引导模型聚焦于预测操作与实际操作之间的差异: \[\mathrm{Loss}=\mathrm{CrossEntropyLoss}(P_{\mathrm{final}},\mathrm{Mask})\]
3.2 自适应尺度加权和模型剪枝
为解决跨尺度权重均衡可能导致特征利用效率低下的问题,同时降低混合模型的参数数量,我们引入自适应加权模块和模型剪枝方法,从而提升预测准确性和计算效率。
3.2.1 规模重要性
权重网络接收原始RGB图像x、其高频分量和低频分量的拼接输入,最终得到尺寸为\(\mathbb{R}^{H\times W\times9}\)的输入。随后网络生成归一化权重向量W,其中每个元素反映了各尺度预测在每个像素上的重要性: \[\begin{matrix}W=\mathrm{WeightingModule}(\{\bf x,{\bf x}_{h},{\bf x}_{l}\}),\\W=\mathbb{R}^{\frac{H}{4}\times\frac{W}{4}\times8}\end{matrix}\]
3.2.2 像素级预测融合
最终的操控区域预测结果通过加权汇总各尺度预测掩膜得出。首先,将各尺度的局部和全局预测掩膜合并形成综合掩膜Pall,其表达式为\(P_{\mathrm{all}}\in\mathbb{R}^{\frac{H}{4}\times\frac{W}{4}\times8}\)。随后进行加权求和计算: \[P_{\mathrm{imal}}=\mathrm{Resize}(\sum_{j=1}^{8}W_{j}\cdot P_{a l l_{j}},H,W)\] 这里,\(P_{\mathrm{imal}}\)是最终预测掩码,调整为原始图像尺寸(H×W)。与之前的预测一样,该掩码与真实掩码进行比较以计算交叉熵损失。
3.2.3 二次修剪的依据
虽然初始训练阶段能让模型收敛并识别不同尺度下潜在的有用特征,但后续分析常会发现某些尺度可能包含冗余甚至噪声信息,这可能会削弱模型的整体效能。因此,有必要通过以下标准来评估每个尺度的贡献度:
首先,通过计算该尺度i中所有像素或特征单元n的权重\(W_{i,n}\)的平均值,得到每个尺度i的平均权重\(\bar{W}_{i}\): \[\bar{W}_{i}=\frac{1}{N}\sum_{n=1}^{N}W_{i,n}\]
接下来,将修剪条件定义如下: \[\mathrm{Pnure\,Condition}\colon\bar{W}_{i}\lt
\epsilon\] 在此,\(\bar{W}_{i}\)表示第i个尺度的平均权重,该权重是基于该尺度内所有N个像素单元计算得出的。如果这个平均权重低于预设阈值\(\epsilon\),则认为对应的尺度对模型贡献微乎其微,随后会被剪枝。这种方法确保模型专注于提供有意义信息的尺度,同时剔除那些对整体性能贡献甚微的尺度。
4. 实验
4.1 实验设置
训练
我们的模型采用标准化的Protocol-CAT数据集进行训练,该数据集由代码库(Ma
et al.
2024)提供。该协议包含已建立的数据集和典型的数据增强方法。所有图像均被调整为512x512像素尺寸。我们在四块英伟达4090显卡上进行了150个训练周期的实验,采用12的批量大小。学习率遵循余弦曲线调度方案(Loshchilov
and Hutter
2017),初始值为1e-4并逐步衰减至最低5e-7,同时设置了2个训练周期的预热期以平稳调整学习率。为防止过拟合,我们使用AdamW优化器并设置权重衰减系数0.05。此外,将累积迭代次数设为2次,通过动态调整批量大小来增强模型对多样化数据输入的泛化能力。
测试
我们采用国际公认的基准测试IMDLBenCo(Ma
et al. 2024)对模型进行评估,测试集包括四个主流数据集:CASIAv1 (Dong,
Wang and Tan 2013)、Coverage (Wen et al. 2016)、NIST16 (Guan et al.
2019)以及Columbia (Hsu and Chang
2006)。这些数据集因其多样化的挑战性而广受认可,是检验图像处理定位方法泛化能力的重要评估平台。
量度
与测试环节保持一致,我们沿用了业界公认的评估基准,采用标准像素级F1分数来衡量定位性能。所有结果均在0.5的默认阈值下计算得出,能够全面反映定位精度的优劣。
4.2 与最新方法比较
为确保评估的准确性,我们使用开源代码在各论文推荐的分辨率下训练模型,并采用CAT-Net(Kwon et al.2022)协议数据集。随后通过F1分数对模型性能进行跨多个权威数据集的基准测试。对比分析涵盖多种方法,包括PSCC-Net(Liu et al. 2022a)、MVSS-Net(Chen et al.2021),、CAT-Net(Kwon et al. 2022)以及Trufor(Guillaroet al. 2023)。
定位结果
在表1中,我们用加粗字体标注了表现最佳的模型,并用下划线标注了次优模型,这些结果均基于所有评估数据集得出。
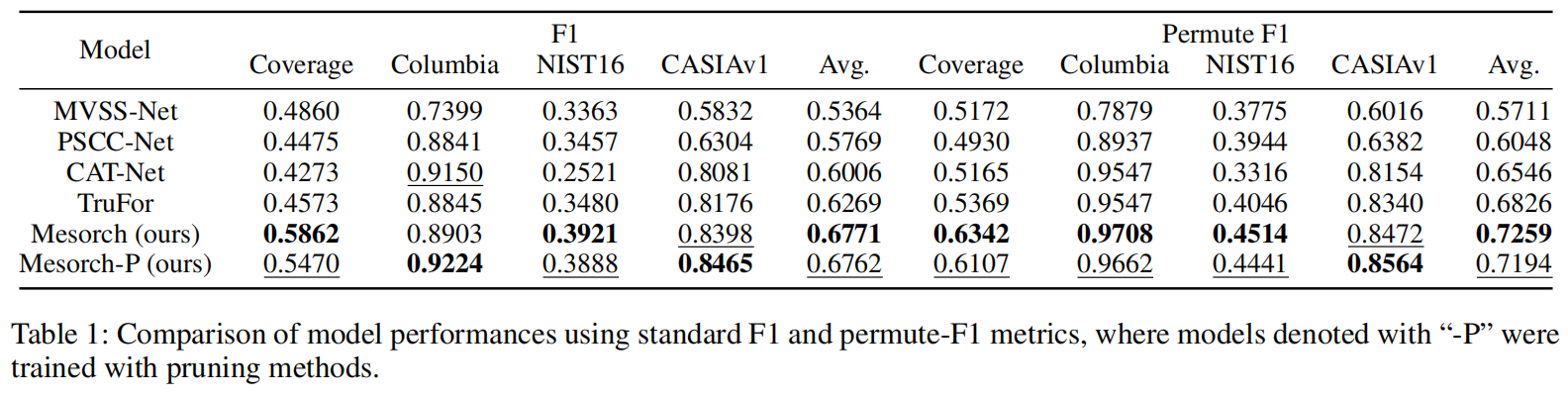
无论是剪枝前还是剪枝后的表现,我们提出的方法始终稳居前列,要么拔得头筹,要么位列第二。这种稳定的表现力充分证明了我们的方法在处理各类图像操作定位任务时具有精准性。此外,图4从定性角度展示了模型成功捕捉到物体布局和介观层面细节的能力,最终生成的被篡改掩膜具有极高的精确度。

鲁棒性能
为评估模型在不同条件下的鲁棒性,我们在CASIAv1数据集上进行了测试,并将结果汇总于表2。
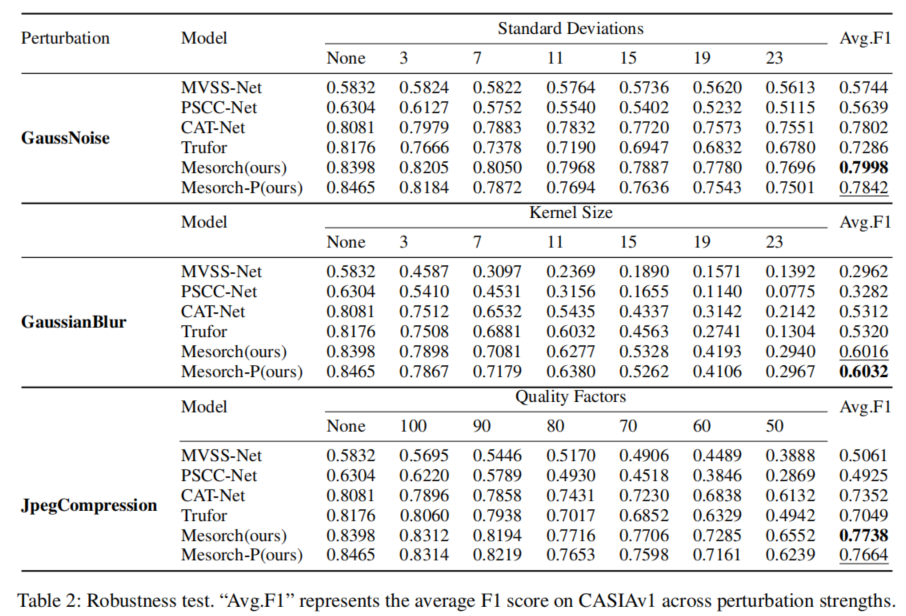
我们引入了标准差各异的高斯噪声、不同核尺寸的高斯模糊处理,以及采用多种质量因子的JPEG压缩作为扰动手段。实验结果表明,我们的模型在这三种扰动方式下均保持了业界领先的鲁棒性表现。值得注意的是,即使经过剪枝处理,我们的方法仍比所有先前的模型保持了更高的鲁棒性,这证明了它在处理各种图像失真方面的有效性。
浮点运算和参数
所有测量的参数数量和浮点运算次数(FLOPs)均基于512x512分辨率和1批次大小进行计算。
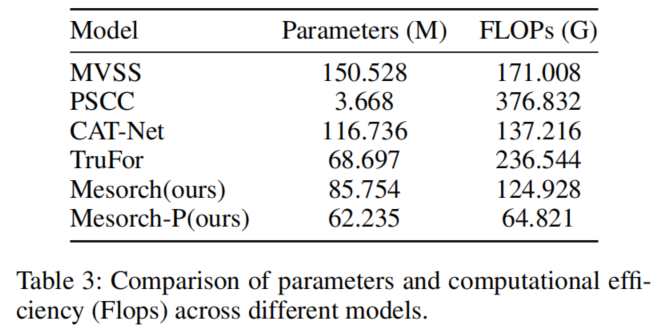
如表3所示,我们的实验结果表明:该模型的FLOPs消耗量低于所有当前最先进的模型,其参数数量仅次于PSCC-Net。此外,通过应用我们的剪枝方法进一步降低了FLOPs和总参数数量,使得本模型相比现有顶尖模型具有显著优势。
4.3 消融研究
对拟定方法的独立评价
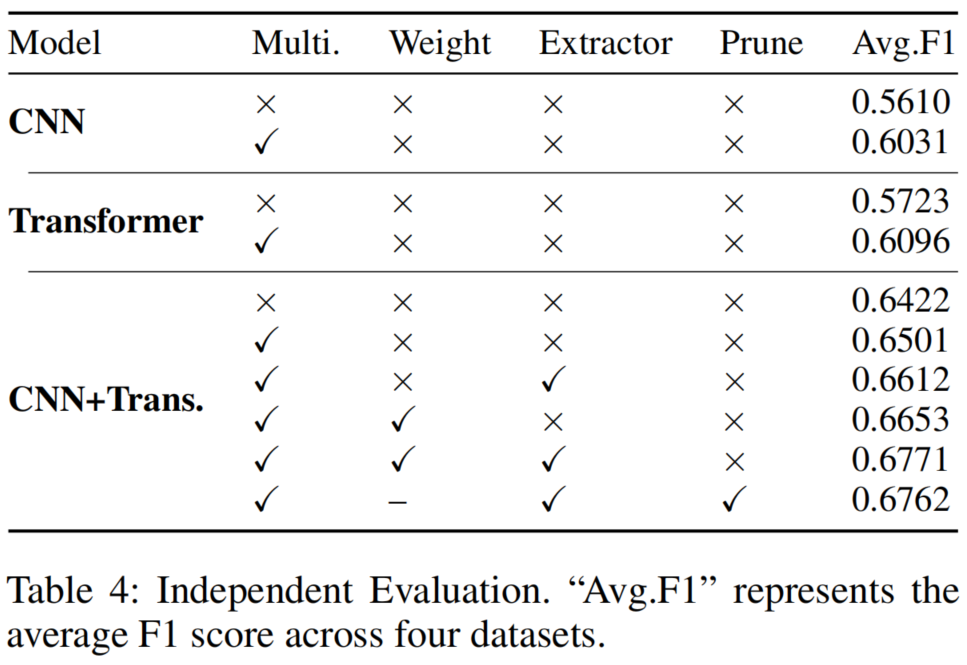
为验证本文提出方法的有效性,我们首先独立评估了CNN的ConvNeXt架构和Transformer的Segformer架构作为基线模型,并在多尺度条件下对其性能进行测试。在确立基线性能后,我们进一步评估了混合模型,逐步整合多尺度方法、加权算法和DCT特征提取技术。同时对剪枝模型进行了测试(如表4所示)。实验结果表明,本文提出的每个组件对于精准定位图像篡改都具有关键作用。
模型体系结构的比较分析
我们通过两种CNN模型(Resnet-50
(He et al. 2016) and ConvNeXt-Tiny (Liu et al.
2022b))与四种Transformer模型(MAE-Base (He et al. 2022), PvT-B3 (Wang et
al. 2022b), Segformer-B3 (Xie et al. 2021),以及SwinTransformer-Base (Liu
et al.
2021))的不同组合,对Mesorch架构的性能进行了评估。各模型间的性能差异总结于第5部分。图5则通过定性分析展示了该架构在不同骨干网络下的表现。

研究结果表明,ConvNeXt与Segformer的组合在宏观定位和微观特征捕捉方面均表现出色,其综合性能超越了其他所有模型组合。
5. 结论
受介观视角启发,本文重新定义了IML任务,旨在协调微观与宏观层面的研究。在此基础上,我们提出Mesorch架构,一种融合卷积神经网络和Transformer模型优势的混合模型,通过动态调整尺度权重,能高效捕捉介观层面的伪影特征。为降低参数量和计算成本,我们还基于该架构引入了两个基准模型。在大规模数据集上的广泛测试表明,我们的方法在F1分数、鲁棒性和运算量等指标上始终保持着业界领先水平。
6. 代码
模型的参数量和FLOPS:
| module | #parameters or shape | #flops | |
按照其主要的成分:
| module | #parameters or shape | #flops | |
其中convnext、segformer为其特征提取器,gate为一个映射
6.1 定义
不含可训练参数的高频和低频信息提取方法:
self.low_dct = LowDctFrequencyExtractor() |
局部特征提取器convnext(模型为convnext_tiny):
self.convnext = ConvNeXt(conv_pretrain) |
全局特征提取器segformer:
self.segformer = MixVisionTransformer(seg_pretrain_path) |
自适应权重模块gate:
self.gate = ScoreNetwork() |
上采样网络,输入为八个特征:
class UpsampleConcatConv(nn.Module): |
将通道数降低为1的网络,前4个卷积层将输入通道数从96减少到1,而后4个卷积层则将输入通道数从64减少到1:
self.inverse = nn.ModuleList([nn.Conv2d(96, 1, 1) for _ in range(4)]+[nn.Conv2d(64, 1, 1) for _ in range(4)]) |
6.2 流程
输入的图片大小是B*3*512*512
计算高频和低频图:
high_freq = self.high_dct(image) |
其中high_freq、low_freq大小是B*3*512*512;input_high、input_low大小是B*6*512*512;input_all大小是B*9*512*512;
分别提取对应的特征:
_,outs1 = self.convnext(input_high) |
其中outs1、outs2都由四个特征构成,inputs由八个特征构成。
for out in outs1: |
通过上采样网络:
x, features = self.upsample(inputs) |
其中,x是features的concat,大小是B*640*128*128
torch.Size([8, 96, 128, 128]) ---------> torch.Size([8, 96, 128, 128]) 不变 |
构建自适应多尺度聚合模块:
gate_outputs = self.gate(input_all) |
其中,gate_outputs的大小为B*8*128*128,为这8个特征的分数
自适应加权:
reduced = torch.cat([self.inverse[i](features[i]) for i in range(8)], dim=1) |
将各个通道数降低为1之后concat,得到reduced,大小是B*8*128*128,
然后乘以特征分数,再求和得到最后的预测图pred_mask,大小是B*1*128*128,
得到对应的损失和预测:
pred_mask = self.resize(pred_mask) |
使用的resize和损失方法为:
self.resize = nn.Upsample(size=(image_size, image_size), mode='bilinear', align_corners=True) |
6.3 实验
首先是实验结果:
"Columbia", "F1": 0.975063915784834, "IOU": 0.9610243780272704, "AUC": 0.9937163561582565 |
如果我使用全0图代替输入的高频图:
high_freq = torch.zeros_like(high_freq, device=high_freq.device) |
如果我使用全0图代替输入的低频图:
low_freq = torch.zeros_like(low_freq, device=low_freq.device) |
如果我使用全0图代替输入的高频图和低频图:
high_freq = torch.zeros_like(high_freq, device=high_freq.device) |
如果我不使用由convnext提取的局部特征分数,只取后四个由segformer提取的全局特征:
reduced = torch.cat([self.inverse[i](features[i]) for i in range(8)], dim=1) |
由此可知由convnext提取的局部特征基本上没用,主要靠segformer提取的多尺度特,接下来对segformer提取的多尺度特征进行测试:
torch.Size([8, 64, 128, 128]) ---------> torch.Size([8, 64, 128, 128]) 不变 |
首先去除 torch.Size([8, 64, 128, 128]) ---------> torch.Size([8, 64, 128, 128]) 特征:
reduced = torch.cat([self.inverse[i](features[i]) for i in range(8)], dim=1) |
去除前两个
reduced = torch.cat([self.inverse[i](features[i]) for i in range(8)], dim=1) |
只保留torch.Size([8, 512, 16, 16]) ---------> torch.Size([8, 64, 128, 128])
reduced = torch.cat([self.inverse[i](features[i]) for i in range(8)], dim=1) |
只保留torch.Size([8, 320, 32, 32]) ---------> torch.Size([8, 64, 128, 128])
reduced = torch.cat([self.inverse[i](features[i]) for i in range(8)], dim=1) |
总结:
- 基于高频信息的全局特征网络(convnext)对于最后的贡献几乎没有
- 多尺度特征中,低等级的大尺度特征[(128, 64, 64), (64, 128, 128)]对于最后的贡献几乎没有
- 基于最后两个尺度[(320, 32, 32), (512, 16, 16)]的结果是最好的,而且(320, 32, 32)的结果要明显好于 (512, 16, 16)
- 对于结果的大部分贡献来源于segformer的(320, 32, 32)尺度的特征,小部分来源于segformer的(512, 16, 16)尺度的特征
ps:不知道是因为交叉熵导致的特征集中还是其他原因。
尝试拿出来:
f7 = gate_outputs[6] * self.inverse[6](self.upsample.upsamples3(outs2[2])) |
ff = torch.cat([self.inverse[6](self.upsample.upsamples3(outs2[2])), |
在完全去除convnext和没有使用的权重之后:
| module | #parameters or shape | #flops | |
这比剪枝狠啊!
ff = torch.cat([self.inverse[6](self.upsample.upsamples3(outs2[2])), |
这样的话其实就是使用segformer提取特征后,对segformer提取的最后两个特征首先上采样然后将通道数降低为1的网络,再乘上一个gate分数网络,最后再相加sigmoid得到预测结果
以上的实验中,并不知道提取的low_freq作用还是segformer网络的作用。
6.4 segformer网络与官方网络的区别
Mlp类、Block类、OverlapPatchEmbed类与原来一样
Attention类在计算完成注意力之后加了一句(attn
= attn.float())
MixVisionTransformer类区别:
- 输入参数的变化,以mit_b3作为对比:
pretrain_path参数:原版没有 ---------> pretrain_path=None |
- 代码变化:
插入了预训练参数的加载:
if pretrain_path is not None: |
去除了原有的初始化代码:
self.apply(self._init_weights) ---------> 去除 |
forward_features方法对输出做了小改变:
return outs ---------> return x,outs |
forward方法变化(为了输出多尺度特征):
def forward(self, x): |
以上便是该文章的segformer网络与官方网络的区别,现在对其区别进行分析:
该文章的segformer网络的输入是input_low = torch.concat([image,low_freq],dim=1),大小是B*6*512*512,所以在加载预训练权重之后对第一层的输入代码进行了更改以适配6通道数的输入。
