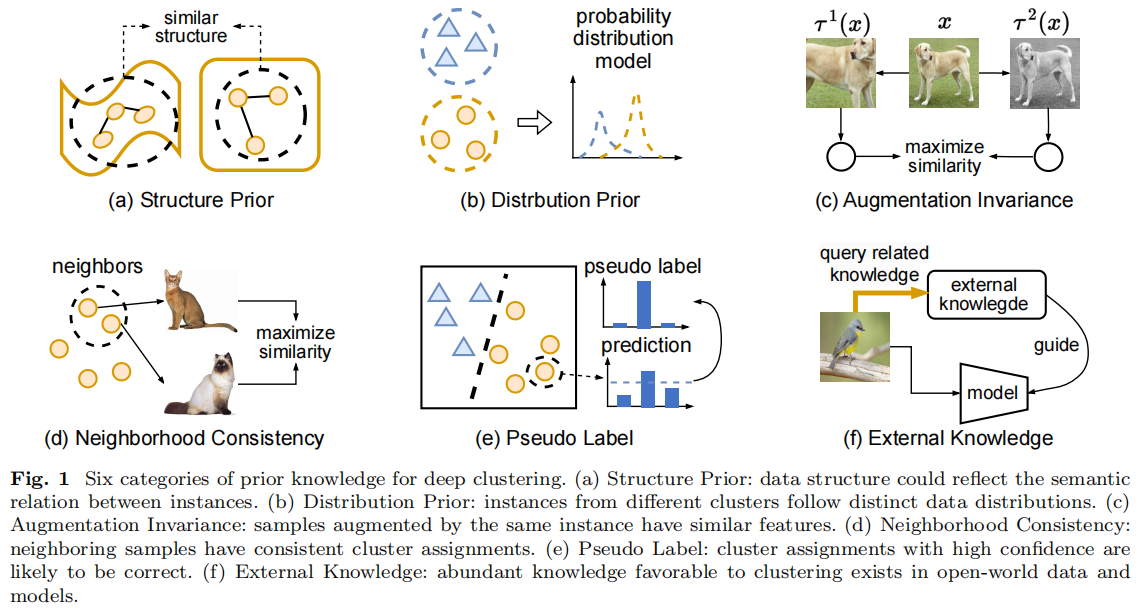
Mind marginal non-crack regions:Clustering-inspired representation learning for crack segmentation
Mind marginal non-crack regions: Clustering-inspired representation learning for crack segmentation
Zhuangzhuang Chen, Zhuonan Lai, Jie Chen, Jianqiang Li *
中国深圳,深圳大学
摘要
裂缝分割数据集在获取真实裂缝或非裂缝标签时,始终致力于实现最大程度的清晰度。然而观察发现,在处理边缘非裂缝区域时,由于对比度不足和纹理异质性,模糊性问题依然难以避免。为解决这一难题,我们提出了一种基于聚类启发的表征学习框架,该框架包含自动裂缝分割的双阶段策略。第一阶段通过预处理步骤实现边缘非裂缝区域的精确定位。为此,我们提出了一种模糊感知分割损失(Aseg Loss,ambiguity-aware segmentation loss),通过学习分割方差来捕捉上述区域的模糊特征,从而帮助裂纹分割模型更精准地定位这些区域。在第二阶段,为学习这些区域的判别性特征,我们设计了聚类启发式损失(CI Loss,clustering-inspired loss),将监督学习模式转变为无监督聚类方式。我们证明了所提出的方法可以在各种数据集和我们构建的CrackSeg5k数据集上超越现有的裂纹分割模型。
1.引言
混凝土结构健康监测在工业场景中具有关键作用[24,29,32,45],其中裂缝分段检测是最后也是不可或缺的环节。随着混凝土结构老化,维护需求日益增加,若处理不当将导致结构健康状况恶化或出现缺陷[20,22]。因此我们认为,在严重劣化发生前及时修复裂缝至关重要,这能有效减轻人工维护负担[5]。然而,由于对比度低、纹理异质性以及没有领域知识的分割区域的不确定性,边缘非裂纹区域的模糊性仍然是不可避免的。考虑到这一点,裂缝的像素级分割仍然是一个挑战[3,7,63]。
当前,深度学习技术的突飞猛进也推动了裂缝分割任务的研究[8,32,41]。例如,DeepCrack
[67]提出了一种基于多阶段融合的裂缝分割方法,该方法源自常用的编码器-解码器架构(SegNet
[2])。受ViT [51]启发,Crackformer
[32]开发出裂缝transformer网络,通过捕捉长程交互来实现细粒度裂缝分割。JTFN
[8]则巧妙利用边界信息,将裂缝边界作为额外监督项应用于裂缝分割任务。然而,这些方法有一个关键的限制:由于边缘非裂纹区域的模糊性,无法提取出区分特征。也就是说,与自然图像中的物体不同,由于裂纹与非裂纹区域之间的对比度较低,可能不存在明显的结构边界。因此,当遇到边缘非裂纹区域的模糊标签时,裂纹分割模型很难提取出判别性特征。为验证这一结论,图1
(b)直观展示了裂纹区域与边缘非裂纹区域的像素特征。可以观察到,在特征空间中投影的各类像素分布范围较广,且裂纹/非裂纹特征相互交织并靠近类别边界。因此,与以往仅关注裂纹边界学习的方法不同,我们认为通过解决边缘非裂纹区域的模糊性问题,仍有提升裂纹分割性能的空间。
本文提出了一种基于聚类的表征学习框架(CIRL),采用两阶段方法解决上述问题。具体而言,第一阶段首先在预处理中定位边缘非裂纹区域。随后,为捕捉这些区域的模糊性特征,我们创新性地提出了基于Wasserstein距离[1]的Aseg损失函数,用于学习分割方差。借助这种方差信息,我们能够更精准地识别出存在模糊性的区域。直观来看,这些模糊区域往往带有模糊标签,这使得裂缝分割模型难以学习到区分性特征。为此,在第二阶段我们提出了新思路:将现有监督学习方法转变为无监督聚类方式,并借鉴共识理论——特征空间中的局部邻近点更可能属于同一簇,其预测结果应比其他特征[10,59]更具相似性。基于上述研究,我们提出了一种受聚类启发的损失函数——CI损失函数,其核心目标是让邻近特征产生相似预测结果,而远距离特征则呈现差异性预测。值得注意的是,该方法可便捷地集成到大多数裂纹分割模型中。此外,通过整合Aseg和CI损失函数,该方法的灵活性显著提升了裂纹分割模型对裂纹区域的精准分割能力。综上所述,本研究的主要贡献包括:
- 据我们所知,这是首个针对边缘非裂纹区域模糊性问题的研究。为此,本文提出了一种受两阶段聚类启发的表征学习(CIRL)框架,旨在摆脱这些模糊标签带来的干扰。
- 本文提出了一种模糊感知分割损失(Aseg Loss),通过学习分割方差,使裂缝分割模型能够捕捉边缘非裂缝区域的模糊性。
- 一种聚类启发式损失函数(CI Loss)通过将现有监督学习转换为模糊区域的无监督聚类方式,实现了CIRL的目标。
- 大量实验验证了所提出的方法在公共数据集和我们构建的CrackSeg5k数据集上的优越性。
2.相关工作
2.1裂缝分割
2.2.裂缝分割损失
2.3.深度聚类学习
鉴于我们的方法旨在对模糊区域进行无监督聚类学习,我们在此简要回顾相关研究进展。当前深度聚类方法大致可分为两类:一类是交替或同步学习特征表示与聚类分配。第一类方法中,DAC
[4]和DCCM
[56]可作为典型范例,它们交替更新聚类分配与样本间相似度。第二类方法则致力于最大化样本与其增强数据之间的互信息[10]。受对比学习启发,许多无监督聚类方法[9,62]通过结合信息非对称编码(InfoNCE)[42]来构建更优的特征空间。值得注意的是,NNCLR
[13]提出了一种创新方案——在对比学习中利用潜在空间中的最近邻作为正样本。但该方法存在一个缺陷:负样本可能包含同类别样本。此外,由于其增强处理仅在图像层面进行,因此难以直接应用于像素级裂缝分割任务。
我们提出的CIRL方法与先前专注于裂纹分割模糊性的方法具有相同的研究目标。但本研究在三个方面独具特色:
(1)本文聚焦于边缘非裂纹区域而非裂纹边界,因此在处理标注错误时,相比基于边缘或边界关键点的方法,我们的方法对误差的敏感度更低;
(2)创新设计的Aseg损失函数能帮助网络学习边缘非裂纹区域的分割差异,从而更精准地定位模糊区域;
(3)CI损失函数专门针对像素级裂纹分割任务中的模糊区域问题,通过构建两组特征集进行无监督聚类学习,突破了现有对比聚类学习中仅使用正负样本的传统框架。
3.方法
本节将介绍我们提出的两阶段CIRL方法,该方法包含两个连续阶段。具体而言,我们首先在第3.1节阐述CIRL的动机。接下来的第一阶段专注于学习边缘非裂纹区域的模糊性特征,从而准确定位这些模糊区域(第3.2节)。随后第二阶段将监督学习转变为无监督聚类学习来处理模糊区域(第3.3节)。图3展示了我们方法的整体框架。
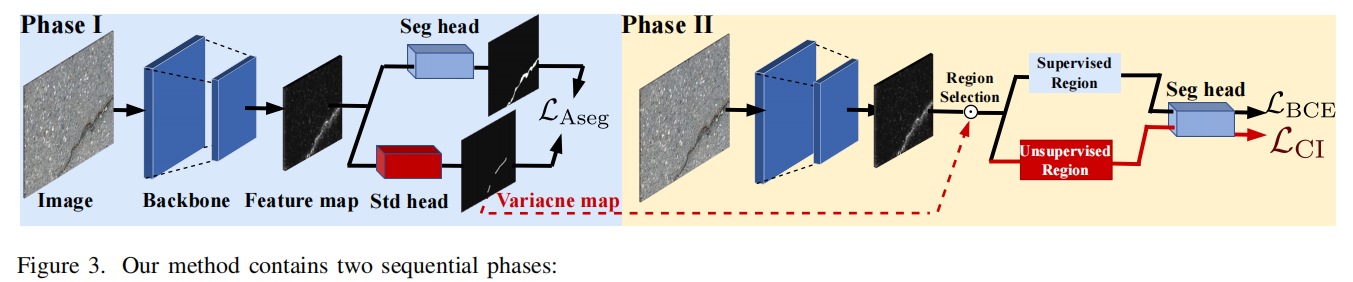
(1)我们的网络首先在模糊感知分割损失(LAseg)的监督下,引入一个标准头来估计标准差并进行分割。随后,学习到的方差图帮助我们在边缘非裂纹区域精确定位模糊区域。(2)我们进一步将现有监督学习问题中这些模糊区域的处理方式转变为无监督聚类模式。随后,我们提出了一种基于聚类启发的损失函数(LCI),帮助网络摆脱模糊标签的干扰并学习判别性特征。移除了标准头模块后,仅需主干网络和分割头即可完成预测任务。因此,我们的框架在推理阶段不会引入额外的计算量和内存占用。
3.1.动机
CIRL从一个直观的想法开始:由于裂缝和非裂缝区域之间的对比度较低,因此在边缘的非裂缝区域中存在歧义。因此,这些区域的标签很可能不明确,使得现有的裂缝分割模型很难学习判别性特征。
为验证这一直觉,我们在CrackSeg5k数据集上开展实验。具体而言,我们首先在二元交叉熵(BCE)损失函数[11]的监督下训练Crackformer
[32]模型,并从随机选取的训练样本中提取裂缝区域及边缘非裂缝区域的像素特征。在预处理阶段,基于真实裂缝分割图\(y^{gt}\),通过OpenCV中的膨胀操作生成边缘非裂缝区域图M,具体流程如下:
\[M=d i l a t e(y^{g t})-y^{g t},\]
其中,dilate(·)表示使用5×5核大小的膨胀操作。随后,我们采用t-SNE
[50]算法对图1
(b)中裂纹像素与非裂纹像素的特征进行可视化处理,并用不同颜色区分显示。可以观察到,在特征空间中部分裂纹像素与非裂纹像素存在纠缠现象。究其原因,部分处于边缘非裂纹区域的像素具有与裂纹像素相似的外观特征。因此,在训练裂纹分割模型时,直接利用这些区域的标签信息是不明智的做法。
在上述讨论的基础上,我们通过额外实验验证了裂缝分割任务中边缘非裂纹区域需要精心设计的解决方案。首先,我们将CrackSeg5k的训练集随机划分为四个子训练集。然后,我们利用上述子训练集以两种方式在BCE损失的监督下训练Crackformer:1)利用边缘非裂纹区域的标签进行训练。2)通过等式1,将边缘非裂纹区域排除在训练之外。这种现象的根源在于:某些模糊区域若直接用于裂缝分割模型训练,可能会产生负面影响;而其他区域则能通过提供像素级的更多训练样本来提升模型性能。为更直观理解这一现象,我们局部模糊区域的可视化结果可参考图2。从直观判断来看,边缘非裂缝区域中的模糊区域需要进一步精确定位,并与其他区域进行区分处理。
3.2.第一阶段:学习边缘非裂纹区域的模糊性
根据前文讨论,在第一阶段,我们的目标是同时估计分割置信度和分割结果,从而捕捉边缘非裂纹区域的模糊性。为此,对于输入图像中位置(i,j)处的像素,我们的网络会预测一个概率分布\(P_{i,j}^{\Theta}(y)\),而非单一标签。在此我们假设每个像素级别的预测标签(即单变量)服从独立高斯分布。由此可得以下公式: \[P_{i,j}^{\Theta}(y)=\frac{1}{\sqrt{2\pi\hat{\sigma}_{i,j}^{2}}}e^{-\frac{\left(y-y_{i,j}^{p}\right)^{2}}{2\hat{\sigma}_{i,j}^{2}}}\] 其中\(\Theta\)是包含主干、seg头和std头的可学习参数集合,如图3所示。其中,\(y_{i,j}^{p}\)和\({\hat{\sigma}}_{i,j}\)分别表示输入图像中位置(i,j)处的预测标签和估计标准差。当\({\hat{\sigma}}_{i,j}\)非常接近0时,表明我们的网络对当前预测标签具有高度置信度。需要说明的是,如图3所示,我们的标准头是通过在主干网络上添加一个全连接层来实现的。因此,相应的真值标签\(y_{i,j}^{gt}\)也可以被表述为高斯分布\({\mathcal N}(y_{i,j}^{gt},\sigma_{i,j}^{2})\),其标准差为\(\sigma_{i,j}^{2}\rightarrow0\)。然后,这个高斯分布可以看作:\(P_{i,j}^{g t}(y)\;=\;\delta\,\left(y-y_{i,j}^{g t}\right)\),其中δ(·)表示Dirac delta函数。然后,所提出的Aseg损失可表述如下: \[\begin{aligned}\mathcal{L}_{\mathrm{Aseg}}&=\sum_{i=1}^{H}\sum_{j=1}^{W}\frac{D_{W}\left(P_{i,j}^{\Theta}(y)||P_{i,j}^{g t}(y)\right)}{\lambda+\hat{\sigma}_{i,j}^{2}}\\&=\sum_{i=1}^{H}\sum_{j=1}^{W}\frac{\|y_{i,j}^{p}-y_{i,j}^{g t}\|_{2}^{2}+\hat{\sigma}_{i,j}^{2}}{\lambda+\hat{\sigma}_{i,j}^{2}}\end{aligned}\] 其中H和W分别表示输入图像的高度和宽度。超参数λ的作用将在后文详细说明。本文采用Wasserstein距离作为距离度量\(D_W(\cdot)\),通过最小化\(P_{i,j}^{\Theta}(y)\)与\(P_{i,j}^{g t}(y)\)之间的距离来实现优化。同时,\(D_{W}\left(P_{i,j}^{\Theta}(y)||P_{i,j}^{g t}(y)\right)\)可以通过以下假设展开:
假设1
如前所述,由于将\(P_{i,j}^{g t}(y)\)视是Dirac
delta函数,其表达式为: \[\delta\left(y-y_{i,j}^{g
t}\right)=\operatorname*{lim}_{\mu\to y_{i,j}^{g
t},\Sigma\to0}\mathcal{N}(\mu,\Sigma),\] 因此\(D_{W}\left(P_{i,j}^{\Theta}(y)||P_{i,j}^{g
t}(y)\right)\)可推导为以下方程式: \[D_{W}\left(P_{i,j}^{\Theta}(y)||P_{i,j}^{g
t}(y)\right)=\|y_{i,j}^{p}-y_{i,j}^{g
t}\|_{2}^{2}+\hat{\sigma}_{i,j}^{2}.\]
证明1
假设我们在\(\mathcal R^n\)空间中有两个多元高斯分布\({\mathcal{N}}_{1}(\mu_{1},\Sigma_{1})\)和\({\mathcal{N}}_{2}(\mu_{2},\Sigma_{2})\),那么这两个分布之间的Wasserstein距离可以推导如下:
\[W_{2}^{2}({\mathcal{N}}_{1}(\mu_{1},\Sigma_{1}),{\mathcal{N}}_{2}(\mu_{2},\Sigma_{2}))=\|\mu_{1}-\mu_{2}\|^{2}+\left(\Sigma_{1}+\Sigma_{2}-2\left(\sqrt{\Sigma_{1}}\Sigma_{2}\sqrt{\Sigma_{1}}\right)^{\frac{1}{2}}\right)\]
现在,通过将上述方程式中的变量\(\delta\left(y-y_{i,j}^{g t}\right)\)和\({\mathcal
N}(y_{i,j}^{gt},\sigma_{i,j}^{2})\)代入,我们可以得到假设1。
值得注意的是,之所以采用Wasserstein距离而非KL散度[17],是因为后者严重依赖于两个分布[1]之间不可或缺的交集。此外,当\(y_{i,j}^{p}\)被准确预测时,即,当\(\|y_{i,j}^{p}-y_{i,j}^{g t}\|_{2}^{2}\rightarrow0\)时,我们的网络预计会产生更小的方差。基于这一考量,我们在公式等式3中新增了项\(\lambda+\hat{\sigma}_{i,j}^{2}\),其作用机制如下:由于边缘非裂纹区域存在模糊性,当预测标签与真实标签不一致时(即\(\|y_{i,j}^{p}-y_{i,j}^{g t}\|_{2}^{2}>\lambda\)时),\({\mathcal{L}}_{\mathrm{Aseg}}\)的最小化过程将促使网络生成更大的方差参数\(\hat{\sigma}_{i,j}^{2}\)。为确保数值稳定性,我们实际采用对数方差参数\(\hat{s}=\log\hat{\sigma}_{i,j}^{2}\)进行预测,并据此重新构建公式等式3如下: \[\begin{aligned}\mathcal{L}_{\mathrm{Aseg}}&=&\sum_{i=1}^{H}\sum_{j=1}^{W}\frac{D_{W}\left(P_{i,j}^{\Theta}(y)||P_{i,j}^{g t}(y)\right)}{\lambda+\exp({\hat{s}})}\\&=&\sum_{i=1}^{H}\sum_{j=1}^{W}\frac{\|y_{i,j}^{p}-y_{i,j}^{g t}\|_{2}^{2}+\exp({\hat{s}})}{\lambda+\exp({\hat{s}})}\end{aligned}\] 现在,由于已学习的方差\(\sigma_{i,j}^{2}=\exp(\hat{s})\),位于(i,j)位置的输入像素将通过以下公式判断是否归类为模糊区域: \[A_{i,j}=\left\{\begin{array}{l l}{1,}&{\mathrm{case}\:\hat{\sigma}_{i,j}^{2}\gt \gamma\;\;\mathrm{and}\;\;M_{i,j}==1}\\ {0,}&{\mathrm{case}\:\hat{\sigma}_{i,j}^{2}\leq\gamma\;\;\mathrm{or}\;\;M_{i,j}==0}\end{array}\right.,\] 其中\(\gamma\)是一个超参数,用作阈值。根据公式等式1,\(M_{i,j}=1\)表示当前像素属于边缘非裂纹区域。
3.3.第二阶段:从监督学习到模糊区域的无监督学习
借助前一阶段的辅助,我们能够定位那些标签存在模糊性的区域。若直接在训练过程中使用这些标签,将会产生不可控的影响。为此,在第二阶段我们提出了聚类启发式损失函数(CI
Loss),其采用无监督特征聚类的方式,其核心思想在于:在特征空间中位置相近/相距较远的特征,其预测结果应呈现一致性/差异性。
给定输入图像\(\mathcal I\),设\(S_{\mathcal
I}\)表示通过等式8算法确定的模糊区域所有像素的特征集合。\({\mathcal F}_m\)和\({\mathcal F}_n\)分别代表\(S_{\mathcal
I}\)表中两个像素的特征值,并对应着预测概率\(p_m\)和\(p_n\)。受文献[14,59]启发,我们定义\(p_{m,n}\)为\({\mathcal F}_m\)和\({\mathcal F}_n\)具有相同预测结果的概率:
\[p_{m,n}=\frac{e^{p_{m}^{T}p_{n}}}{\sum_{\mathcal{F}_{q}\in
S_{\overline{r}}}e^{p_{m}^{T}p_{q}}}.\] 对于\(S_{\mathcal I}\)中的每个特征\({\mathcal
F}_m\),我们定义了两个集合:邻近特征集\({\mathcal C}_m\)和远端特征集\({\mathcal
O}_m\)。前者通过余弦相似度作为距离度量,从\(S_{\mathcal I}\)中选取\({\mathcal
F}_m\)的K个最近邻;后者则是通过排除\({\mathcal C}_m\)和\({\mathcal F}_m\)后剩余的\(S_{\mathcal
I}\)特征构建而成。回到研究初衷,对于每个特征\({\mathcal F}_m\)而言,其在\({\mathcal O}_m\)中的预测结果应比在\({\mathcal
C}_m\)中更显著地表现出不一致性。基于此,我们定义了\({\mathcal F}_m\)与\({\mathcal C}_m\)之间的似然函数: \[P\left({\mathcal
C}_m\mid{\mathcal{F}}_{m},\theta_{\mathcal{B}},\theta_{\mathcal{S}}\right)=\prod_{\mathcal{F}_{n}\in
{\mathcal C}_{m}}p_{m,n}=\prod_{\mathcal{F}_{n}\in {\mathcal
C}_{m}}{\frac{e^{p_{m}^{T}p_{n}}}{\sum_{\mathcal{F}_{q}\in {S}_{\mathcal
I}}e^{p_{m}^{T}p_{q}}}},\] 其中\(\theta_{\mathcal{B}}\)和\(\theta_{\mathcal{S}}\)分别表示网络中主干和seg头部的参数。类似地,\({\mathcal{F}}_{m}\)与\({\mathcal{O}}_{m}\)之间的似然函数可定义如下:
\[P\left({\mathcal
O}_m\mid{\mathcal{F}}_{m},\theta_{\mathcal{B}},\theta_{\mathcal{S}}\right)=\prod_{\mathcal{F}_{n}\in
{\mathcal O}_{m}}p_{m,n}=\prod_{\mathcal{F}_{n}\in {\mathcal
O}_{m}}{\frac{e^{p_{m}^{T}p_{n}}}{\sum_{\mathcal{F}_{q}\in {S}_{\mathcal
I}}e^{p_{m}^{T}p_{q}}}},\]
现在,我们可以通过最小化以下负对数似然函数来实现我们的聚类启发式损失的目标:
\[\psi({\mathcal C}_m,{\mathcal O}_m)=-l o
g{\frac{P\left({\mathcal
C}_m\mid{\mathcal{F}}_{m},\theta_{\mathcal{B}},\theta_{\mathcal{S}}\right)}{P\left({\mathcal
O}_m\mid{\mathcal{F}}_{m},\theta_{\mathcal{B}},\theta_{\mathcal{S}}\right)}}.\]
注意到当\(S_{\mathcal
I}\)非常大时,计算上述方程是低效的甚至是不现实的,考虑到这一点,我们通过以下命题推导出一个上界作为替代方案。
假设2
假设\(|{\mathcal O}_m|\)显著大于\(|{\mathcal C}_m|\),那么我们得到一个由\(\psi({\mathcal C}_m,{\mathcal
O}_m)\)给出的上界。 \[\begin{aligned}
&
\psi(\mathcal{C}_{m},\mathcal{O}_{m})=-log\frac{P\left(\mathcal{C}_{m}\mid\mathcal{F}_{m},\theta_{\mathcal{B}},\theta_{\mathcal{S}}\right)}{P\left(\mathcal{O}_{m}\mid\mathcal{F}_{m},\theta_{\mathcal{B}},\theta_{\mathcal{S}}\right)}
\\ &
\leq-\sum_{\mathcal{F}_{n}\in\mathcal{C}_{m}}p_{m}^{T}p_{n}+\frac{|\mathcal{C}_{m}|}{|\mathcal{O}_{m}|}\sum_{\mathcal{F}_{k}\in\mathcal{O}_{m}}p_{m}^{T}p_{k}+(|\mathcal{C}_{m}|-|\mathcal{O}_{m}|)\log|S_{\mathcal{I}}|
\\ &
=\overline{\psi}(\mathcal{C}_{m},\mathcal{O}_{m})\end{aligned}\]
证明2
根据等式10-12,我们有\(\psi({\mathcal C}_m,{\mathcal O}_m)\):
\[\begin{aligned} & \psi({\mathcal
C}_m,{\mathcal O}_m)\\ &
=-\sum_{\mathcal{F}_{n}\in\mathcal{C}_{m}}p_{m}^{T}p_{n}+\sum_{\mathcal{F}_{k}\in\mathcal{O}_{m}}p_{m}^{T}p_{k}+(|\mathcal{C}_{m}|-|\mathcal{O}_{m}|)\log\left(\sum_{\mathcal{F}_{q}\in
S_{\mathcal{I}}}e^{p_{m}^{T}p_{q}}\right) \\ &
\leq\sum_{\mathcal{F}_{n}\in\mathcal{C}_{m}}p_{m}^{T}p_{n}+\sum_{\mathcal{F}_{k}\in\mathcal{O}_{m}}p_{m}^{T}p_{k}+(|\mathcal{C}_{m}|-|\mathcal{O}_{m}|)\left(\sum_{\mathcal{F}_{q}\in
S_{\mathcal{I}}}\frac{p_{m}^{T}p_{q}}{|S_{\mathcal{I}}|}+\log|S_{\mathcal{I}}|\right)
\\ &
\approx\sum_{\mathcal{F}_{n}\in\mathcal{C}_{m}}p_{m}^{T}p_{n}+\sum_{\mathcal{F}_{k}\in\mathcal{O}_{m}}p_{m}^{T}p_{k}+(|\mathcal{C}_{m}|-|\mathcal{O}_{m}|)\left(\sum_{\mathcal{F}_{q}\in\mathcal{O}_{m}}\frac{p_{m}^{T}p_{q}}{|\mathcal{O}_{m}|}+\log|S_{\mathcal{I}}|\right)
\\ &
=\sum_{\mathcal{F}_{n}\in\mathcal{C}_{m}}p_{m}^{T}p_{n}+\frac{|\mathcal{C}_{m}|}{|\mathcal{O}_{m}|}\sum_{\mathcal{F}_{k}\in\mathcal{O}_{m}}p_{m}^{T}p_{k}+(|\mathcal{C}_{m}|-|\mathcal{O}_{m}|)\log|S_{\mathcal{I}}|
\\ &
=\overline{\psi}(\mathcal{C}_{m},\mathcal{O}_{m}),\end{aligned}\]
其中第一个不等式通过满足Jensen不等式成立,因为对数函数log(·)是凹函数。
由于我们有\(S_{\mathcal{I}}\approx \mathcal{C}_{m}\cup
\mathcal{O}_{m}\)且\(|{\mathcal
O}_{m}|\gg|\mathcal C_{m}|\),因此在假设\(S_{\mathcal{I}}\)可近似为\({\mathcal
O}_{m}\)的情况下,我们得到了第三个方程。最后,考虑到整个特征集\(S_{\mathcal{I}}\),我们定义了如下基于聚类的损失函数:
\[{\mathcal{L}}_{\mathrm{CI}}={\frac{1}{|S_{\mathcal{I}}|}}\sum_{\mathcal{L}_{m}\in
S_{\mathcal{I}}}\overline\psi({\mathcal C}_m,{\mathcal O}_m).\]
借助\({\mathcal{L}}_{\mathrm{CI}}\),我们能够对模糊区域进行无监督聚类学习。同时,对于剩余区域,我们采用常用的BCE损失函数进行监督训练。通过这种方式,裂缝分割模型能够摆脱模糊标签的干扰,学习到具有区分性的特征。最终,我们的整体损失函数可表示为:
\[\mathcal{L}_{\mathrm{total}}=\mathcal{L}_{\mathrm{BCE}}+\beta\mathcal{L}_{\mathrm{Cl}},\]
其中标量β用于平衡两个损失函数。
4.实验
核心实验方案详见第4.1节。为确定CIRL模型中λ、γ和β参数的最佳取值,我们在第4.2节通过多组实验进行验证。为验证方法有效性,我们不仅在第4.3节与现有裂纹分割模型展开对比,还在第4.4节与其他前沿分割损失函数展开横向比较。特别值得关注的是,第4.5节的消融实验首先验证了我们提出的模糊感知分割损失相较于现有不确定性方法的优势,随后通过实证表明,这种受聚类启发的损失函数在裂纹分割任务中显著优于现有的无监督聚类学习方法。
4.1.实验设置
在本文中,我们基于我们的CrackSeg5k数据集、两个公共的裂缝分割数据集、一个血管分割数据集以及相应的实现细节进行了广泛的实验。
实施细节
我们在PyTorch2框架下使用单块NVIDIA
RTX
3090显卡进行实验。参照前人研究[8],我们采用水平翻转、随机裁剪和随机旋转(90◦、180◦、270◦)作为数据增强策略。同时,我们沿用了[8]的训练设置——所有样本在训练阶段均被裁剪为256×256尺寸。优化器选用Adam
[21],初始学习率设为10−3,权重衰减系数为5×10−4,小批量大小为2。针对这四个数据集,模型总训练周期为2000个epoch。此外,在训练初期,若标准头未正确学习,所学方差信息量不足。因此,前1000个epoch作为第一阶段,之后模型采用LBCE与LCI联合监督机制(参考等式16)。
评估指标
为评估裂纹分割的像素级准确率,我们参照现有研究[8,19,47]采用F1分数、精确率和召回率作为评估指标。需要特别说明的是,精确率和召回率是通过逐像素比对预测掩膜与真实掩膜来计算得出的。F1分数的计算公式为:\(F_{1}=2\frac{P r e c t s i o n\times R e c a l
l}{P r e c t s i o n+R e c a l l}\)。
4.2.超参数灵敏度研究
本文引入了四个超参数:λ用于帮助模型捕捉模糊区域,γ用于在第一阶段定位模糊区域,K用于定义邻近区域集合的大小,β则用于在第二阶段平衡BCE损失和CI损失。图4展示了基于JTFN [8]作为基础分割模型,在CrackSeg5k数据集上的超参数敏感性研究结果。
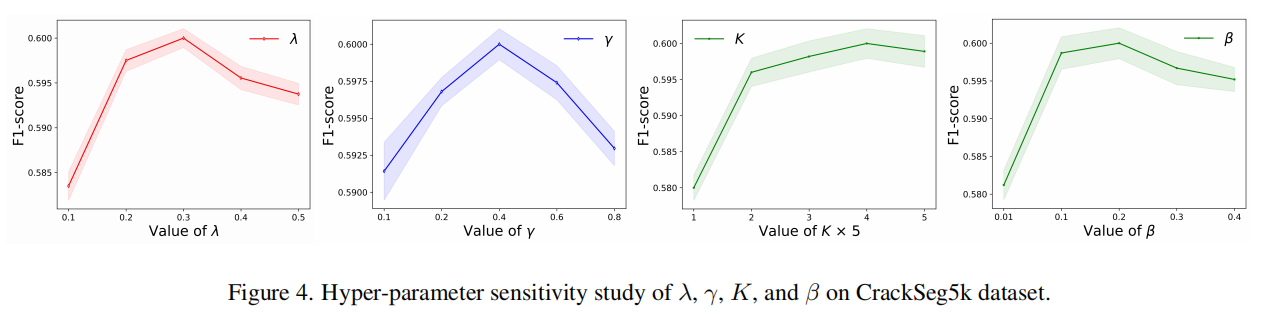
可以观察到,四个超参数λ、γ、K和β在较大范围内仅分别比最高值降低了1.5%、0.8%、2.0%和1.8%的F1分数,这表明我们提出的方法在实际应用中具有潜力。根据这些观察结果,我们在后续实验中设定λ = 0.3、γ = 0.4、K=4×5和β = 0.2。
4.3.裂缝分割模型的比较
4.4.分割损失比较
4.5.消融研究
5.结论
综上所述,边缘非裂纹区域的模糊性会制约当前最先进的裂纹分割模型性能。本文提出了一种基于两阶段聚类启发式表征学习(CIRL)框架,旨在实现更精准的像素级裂纹分割。该框架包含模糊感知分割损失(Aseg Loss),促使网络学习预测每个像素的分割方差,从而进一步精确定位模糊区域。随后引入聚类启发式损失(CI Loss),用于学习上述区域的判别特征。实验结果表明,我们的方法在裂纹分割任务中超越了现有最优方案和传统损失函数。鉴于先前研究在频域学习判别特征方面表现优异[39,57],我们计划进一步探索基于特征的数据增强技术[6]和神经元脉冲网络架构[27,28]在裂纹分割中的应用潜力。