PRCL:Probabilistic Representation Contrastive Learning for Semi-Supervised Semantic Segmentation

PRCL: Probabilistic Representation Contrastive Learning for Semi-Supervised Semantic Segmentation (IJCV 2024)

Boosting Semi-Supervised Semantic Segmentation with Probabilistic Representations (AAAI2023)

Haoyu Xie1,3 · Changqi Wang1 · Jian Zhao2 · Yang Liu3 · Jun Dan4 · Chong Fu1 · Baigui Sun3

1计算机科学与工程学院，东北大学，沈阳，中国
2智能博弈与决策实验室，北京，中国
3阿里巴巴达摩学院，阿里巴巴集团，杭州，中国
4浙江大学信息科学与电子工程系，杭州，中国

摘要

​  在对比学习框架下，半监督语义分割（S4）已取得重大突破。然而由于标注数据有限，模型自身生成的无标签图像引导信息难免存在噪声干扰，影响无监督训练效果。为解决这一问题，我们提出了一种基于概率表示对比学习（PRCL）框架的鲁棒性增强方案，显著提升了无监督训练的稳健性。通过多元高斯分布将像素级表征建模为概率表示（PR），并动态调节模糊表征的贡献度，有效规避了对比学习中引导信息失准的风险。此外，我们整合整个训练过程中的所有PR数据构建全局分布原型（GDP）。该模型不仅具备对表征瞬时噪声的鲁棒性，还能捕捉表征类内的内在差异。基于GDP生成的虚拟负样本（VNs）进一步融入对比学习流程。在两个公开基准数据集上的大量实验表明，PRCL框架展现出显著的优越性。

1.引言

​  语义分割是计算机视觉领域的基础性任务，其核心目标是预测每个像素的类别。通过在大规模标注图像上训练分割模型(Hoffman et al., 2016; Chen et al., 2018; Xie et al.,2021)，已取得显著进展，但这一过程需要耗费大量人力成本。半监督语义分割（S4）通过在训练过程中引入未标注图像，结合对抗训练(Hung et al., 2018)、一致性正则化(Peng et al., 2020)和自训练机制(Tarvainen & Valpola 2017)，有效提升了分割模型的性能，从而缓解了标注图像的短缺问题。
​  自训练是一种广为人知的范式，在S4任务中被广泛采用。它通过利用在标注图像上预训练的模型，为未标注图像生成预测结果，即伪标签。这些伪标签与注释一起被用作重新训练模型的指导。近期研究者们提出了强大的新方法，将像素级对比学习引入自训练范式，旨在探索不仅单张图像局部语义信息，还包括小批量图像乃至整个数据集的语义特征。该方法通过将像素投影到潜在空间中的表征实现这一目标：同类表征会聚集在类质心（即原型）周围，而异类表征（即负样本）则会被有效分离。在半监督学习框架下，对比学习中未标注图像的语义引导来源于训练过程中的伪标签。因此，伪标签的质量对对比学习至关重要——若伪标签存在偏差，会导致将表征错误分配到错误类别，从而引发潜在空间的紊乱。现有方法已尝试通过置信度(Liu et al., 2022)或熵值(Feng et al., 2022)来优化这些伪标签。尽管这些技术在提升伪标签质量、消除不准确标签方面已初见成效，但其依赖的策略仍显脆弱，难以彻底解决伪标签中固有的噪声和错误问题。面对这些挑战，我们的目标是增强表征的鲁棒性，使其即使在存在不准确伪标签的情况下也能更高效地运作。通过强化表征对不完美引导的适应能力，我们成功提升了基于对比度的S4方法的整体性能与可靠性。
​  与传统确定性表示建模方法（即将表征映射到潜在空间中的确定性点）不同，我们提出的方法通过将表征视为具有可学习参数的随机变量，开创了全新的研究视角，这种创新被称为概率表示（PR）。具体而言，我们采用多元高斯分布来建模表征，从而获得分布原型。

image-20250904231230426

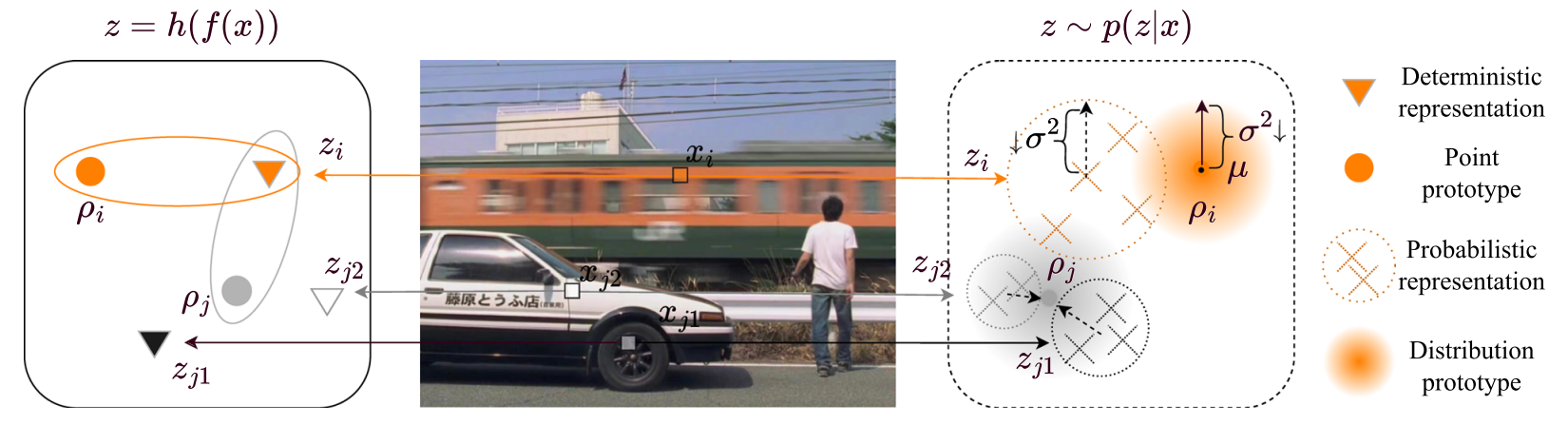
图1两种表征类型与原型的区分。点型原型指确定性表征的原型，分布型原型指概率性表征的原型。我们引入概率概念，将表征视为多元高斯分布，这与传统表征方式不同。这种概率性表征能在一定程度上消除表征原型映射的模糊性，并增强模型在训练模糊像素时的鲁棒性。

​  如图1所示，这种概率建模体现在表达式\(z\sim p(z|x)\)中。模糊列车车厢xi的像素在包含两个分量的潜在空间中映射为zi：最可能的表示μ（均值）和分布的概率σ2（方差）。类似地，车厢x j1和x j2的像素分别映射为zj1和zj2。作为对比，确定性映射显示为\(z=h(f(x))\)。当表示zi到原型ρi的距离与zi到ρj的距离相同时，确定性表示在将zi映射到ρi或ρj时会出现歧义。相反，在概率表示的潜在空间中，由于ρi的σ2值小于ρj，因此zi被映射到ρi。值得注意的是，σ2与概率成反比，这意味着根据概率从zi到ρi的映射比映射到ρj更为可靠（图2）。

image-20250904231716518

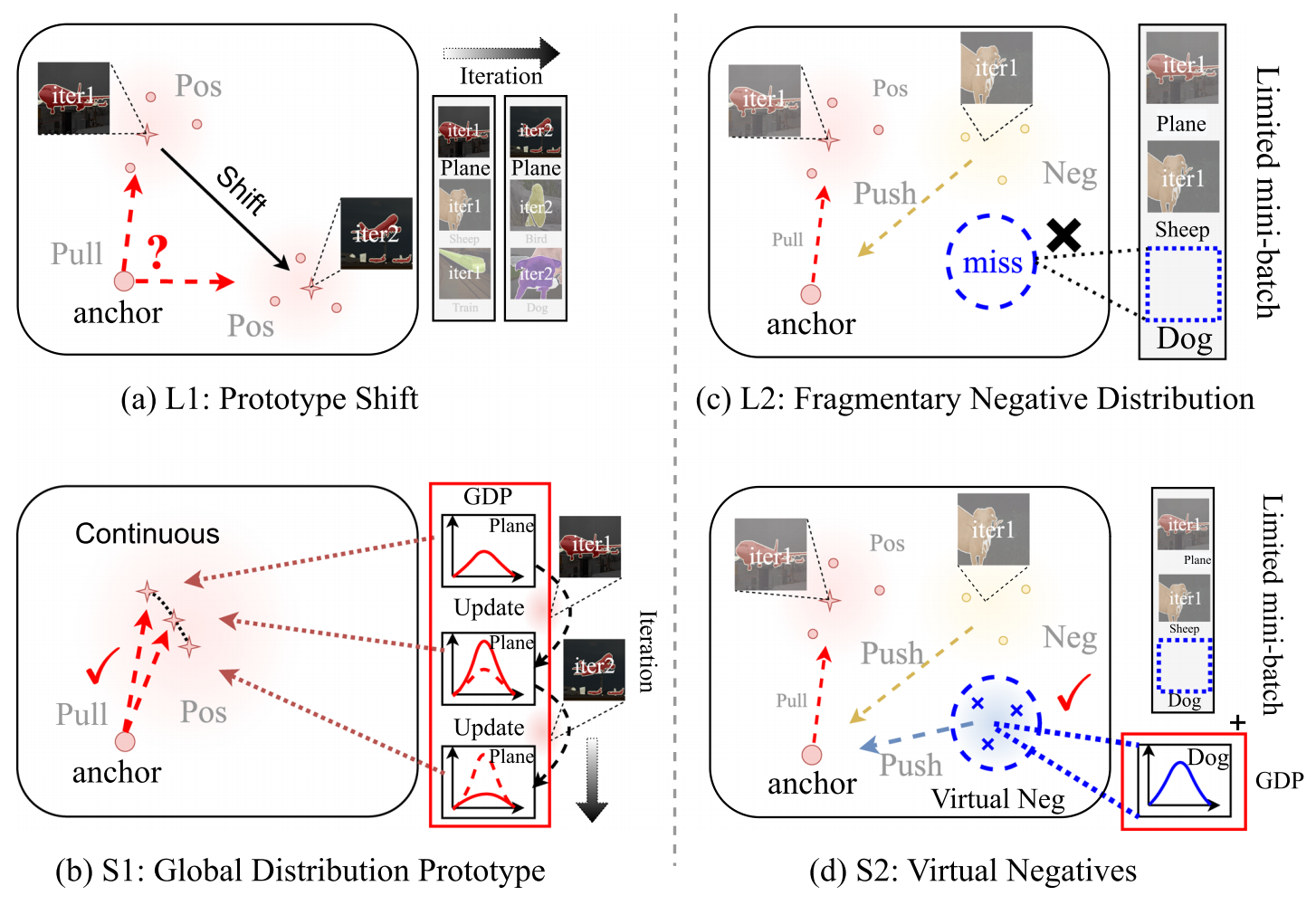
图2 我们的PRCL框架通过提出的全局分布原型和虚拟负样本，有效解决了原型偏移及碎片化负样本分布（L1和L2）带来的负面影响。（S1和S2）

​  当前基于对比度的S4方法存在一个明显缺陷：仅关注当前迭代阶段的对比度。具体来说，这类方法通过聚合当前迭代中同类表征的语义信息来生成原型。由于伪标签的不准确性和类内方差导致表征差异，这种做法容易引发相邻迭代中的原型偏移现象。我们认为原型一致性对于建立表征聚合的稳定方向至关重要。此外，由于在仅考虑当前迭代对比度时，负样本表征来自当前小批量数据，而小批量数据规模有限，导致负样本表征的分布呈现碎片化特征。一些研究方法(Alonso et al., 2021; Hu et al., 2021)利用记忆库策略来弥补片段分布的不足，该策略将表征存储在外部记忆中，并在构建负样本分布时从中采样。然而，密集的像素级表征会导致显著的内存开销和高昂的计算成本。为突破这些局限，我们从全局视角重新构思像素级对比学习方法，基于概率化表征构建全局分布原型（GDP）。与传统原型仅表示当前小批量中同类语义信息不同，GDP通过在训练迭代过程中聚合表征，并采用当前迭代的原型作为贝叶斯估计（Vaseghi，2008）的观测值进行更新。通过在训练过程中运用GDP（生成对抗概率）来衔接迭代阶段，我们的方法使原型能够承受表征中的瞬时噪声，并适应同类表征间的内部差异。因此，原型在迭代过程中保持更高的一致性，为相同表征的聚合提供了稳定方向。与传统通过构建记忆库提供大量负样本的方法不同，我们提出了一种名为虚拟负样本（VN）的创新策略。通过借鉴GDP模型中的参数重配置技巧，我们开发了虚拟神经网络（VN）架构，并借助虚拟半径参数在模型紧凑性与多样性之间取得平衡。值得注意的是，相较于传统记忆库方案，我们的虚拟神经网络将GPU内存占用从2.63GB大幅压缩至42KB，同时训练速度提升22.23%。最关键的是，我们提出的虚拟神经网络策略在性能表现上超越了传统记忆库方案。
​  本研究基于我们先前的会议版本[1]，针对当前迭代仅考虑对比度的局限性展开改进，包括相邻迭代间的原型偏移和负分布碎片化问题。具体而言，我们提出采用更新策略的GDP算法，并结合虚拟网络（VN）技术来保持原型一致性并补偿负分布碎片化。简而言之，我们的主要贡献体现在四个方面：

• 我们引入了概率表示，并提高了对比学习中表示的鲁棒性，这减轻了不准确的伪标签的负面影响。
• 我们构建了全局分布原型和虚拟负体，以弥补小批量带来的缺陷，这比传统的内存银行策略更节省内存，速度更快。
• 在PASCAL VOC 2012和Cityscapes上的大量实验证明了我们提出的方法的有效性。
• 我们进行了全面的消融研究和对概率表示、全局分布和虚拟负样本的深入分析，这表明我们的方法不仅提高了S4中分割模型的鲁棒性和性能。

2.相关工作

2.1.半监督语义分割

2.2.像素级对比学习

​  与传统的实例级对比学习(Wu et al.,2018; Ye et al., 2019; Chen et al., 2020; He et al., 2020; Grill et al., 2020; Xiao et al., 2022)不同，后者将每张图像视为独立类别并通过多视角区分。在像素级对比学习中(Wu et al.,2018; Ye et al., 2019; Chen et al., 2020; He et al., 2020; Grill et al., 2020; Xiao et al., 2022),，密集的像素级表征通过语义引导（即标签或伪标签）进行区分。然而在半监督场景下，标注图像的可用性有限，多数像素分类依赖伪标签，这可能导致误差并破坏潜在空间。为解决这些问题，先前方法(Liu et al., 2022; Alonso et al., 2021; Wang et al.,2022)尝试通过阈值采样策略优化伪标签。相比之下，我们的方法专注于提升表征质量并适应不准确的伪标签，而非单纯过滤它们。通过强化表征质量的提升，我们旨在缓解伪标签的负面影响，构建更稳健有序的潜在空间。
​  像素级对比学习的核心在于将同类特征聚合到原型（类质心）中，并将其与负样本（不同类别特征）区分开来。由于GPU内存有限，多数方法(Liu et al., 2022; Wang et al., 2022)的原型仅收集当前迭代的语义信息，忽视了整个数据集的全局语义特征。为解决这一局限，部分研究提出使用记忆库存储历史迭代特征(Hu et al., 2021)，或采用指数移动平均法（EMA）更新原型(Xu et al., 2022; Zhou et al., 2022)。本方法创新性地引入全历史特征的综合策略，突破了传统限制。针对负样本问题，现有方法(Liu et al., 2022)通常从当前迭代采样，但受限于批量大小，可能导致特征覆盖不全，引发碎片化的负样本分布。为解决此问题，部分研究通过引入记忆库(Wang et al., 2023; Alonso et al., 2021; Wang et al., 2022)或概率化近似负样本分布(Xie et al., 2023)来缓解。本方法则通过自动生成特征来补偿负样本分布，既节省内存又降低计算成本。

2.3.概率嵌入

3.方法

​  在S4任务中，我们可以构建一个包含Nl对图像及其对应像素级标签的标注数据集\({\mathcal D}_l=\{(x_{i}^{I},y_{i}^{I})\}_{i=1}^{N_l}\)，以及仅含Nu张未标注图像的未标注数据集\({\mathcal D}_u=\{x_{i}^{u}\}_{i=1}^{N_u}\)。我们的目标是使用这两个数据集训练分割模型。基础分割模型包含编码器f（·）和分割头g（·），我们采用教师-学生框架，并将像素级对比学习融入框架设计，具体方法详见第3.1节。

image-20250905113253704

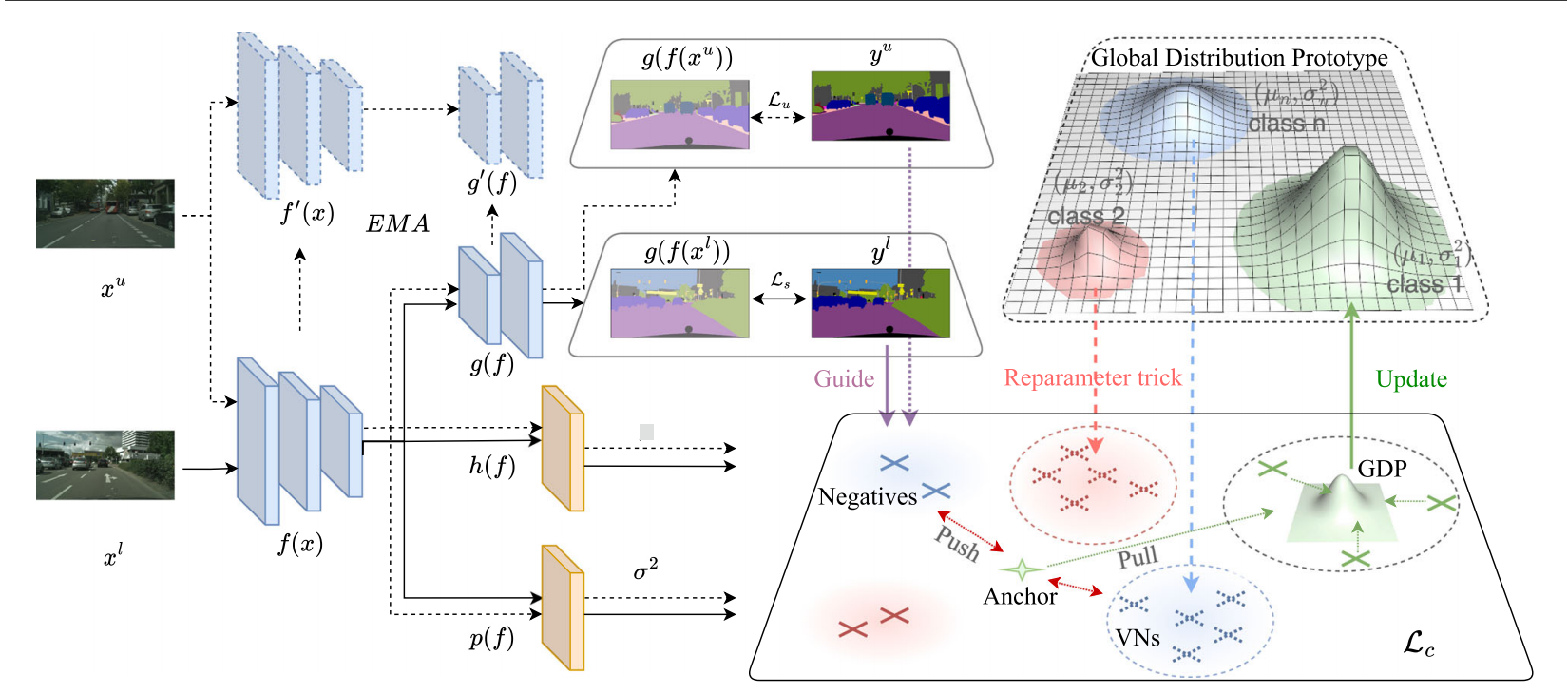
图3 PRCL整体框架示意图。训练流程包含两个输入流：带标签图像（黑色箭头）和未标注图像（黑色虚线箭头）。在像素空间中，模型通过真实标签\(y^{l}\)与原始伪标签\(y^{u}\)的组合进行引导。在潜在空间中，模型通过h（·）和p（·）两个头将像素映射为概率表示\(z\sim N(\mu,\sigma^{2})\)。GDP存储于原型级字典中，并通过局部原型进行更新。我们从GDP生成虚拟负样本(VN，虚线叉号），用于对比损失Lc的计算。

3.1. MT和对比学习

​  标准的师生模型架构包含两个具有相同结构的分割模块，分别称为学生模型和教师模型。我们将学生模型中的编码器和分割头标记为\(f(\cdot)\)、\(g(\cdot)\)型中的对应部分则表示为\(f^{\prime}(\cdot)\)、\(g^{\prime}(\cdot)\)。学生模型通过随机梯度下降（SGD）优化参数以最小化损失函数L，而教师模型的参数则采用学生模型参数的指数移动平均（EMA）进行更新。在无监督训练阶段，学生模型使用的伪标签\(y_i^u\)是基于教师模型输出的logits生成的，即\(p_{i}^{u}=g^{\prime}(f^{\prime}(x_{i}^{u}))\)，其数学表达式为： \[y_{i}^{u}=\mathbf{1}_{c}(\arg\operatorname*{max}_c\{p_{i,c}^{u}\}_{c\in C}),\] ​  其中\(p_{i,c}^{u}\)表示第c个维度上的\({\mathbf p}_{i}^{u}\)值，\(\mathbf{1}_{c}(\cdot)\)表示类别c的一热编码，C表示数据集中的总类别数。为了进一步对模型输出进行正则化处理，为了在潜在空间中对模型的输出进行额外的正则化，最近的方法(Alonso et al., 2021; Liu et al., 2022; Wang et al., 2022, 2021; Hu et al., 2021; Jiang et al., 2022;Wang et al., 2023)将对比学习引入到师生模式中。具体而言，学生模型引入了一个表示头h（·），用于将像素映射到表示空间，即\(z_{i}=h(f(x_{i}))\)。同类表示会被聚合到原型ρ中，而不同类别的表示则通过对比损失（如信息NCE）进行区分。每个类别的原型ρ是通过整合同类表示的语义信息获得的。对比学习的语义引导同样来源于\(y_i^l\)和\(y_i^u\)。

​  讨论
​  本文指出，当前基于像素级对比学习的S4模型存在两大潜在缺陷：
​  (1)当伪标签不准确时，模型的鲁棒性会显著下降。由于伪标签\(y_i^u\)完全依赖教师模型分割头g（·）的预测结果，而教师模型的认知能力存在局限性，必然会产生错误标签。尽管通过采用精细采样策略可以提升伪标签质量，但其本质缺陷仍难以彻底消除。如果在\({\mathcal D}_u\)训练中直接将这些不准确的伪标签作为监督信息使用，将会误导模型。然而，在不准确的伪标签环境下学习鲁棒对比式S4模型这一策略，却长期被忽视且未被深入探索。
​  (2)原型发生偏移，负分布不完整。在近期研究中，原型ρ通常被定义为当前迭代中同类表示的平均值。然而，由于伪标签存在偏差和类内方差的影响，同一类别的表示在不同迭代中可能出现显著差异，导致原型位置发生剧烈偏移，这种现象被称为原型漂移。我们认为，原型的这种偏移不仅阻碍了对同类表示进行一致聚合的方向指引，还会造成潜在空间的无序状态。此外，由于负样本来自当前小批量数据，有限的小批量规模会导致对比学习过程中当前迭代的负样本分布呈现碎片化特征。尽管已有研究尝试通过建立记忆库存储历史迭代的表示并从中采样负样本来解决这一局限，但该策略会带来高昂的内存占用和计算成本。
​  为解决这些局限性，我们构建了一个能有效应对伪标签不准确问题的框架。该框架的表征模型采用高斯分布建模（详见第3.2节），通过构建全局分布原型（GDP）来保持原型一致性（第3.3节），并基于GDP生成虚拟负样本（VN）以弥补碎片化负样本分布的不足（第3.4节）。

3.2. 概率表示

​  在本节中，我们将详细阐述构建概率表示的方法及其相似度测量机制。
​  我们将像素点xi映射到表示zi的概率记作\(p(z_{i}|x_{i})\)，并定义该表示为遵循该分布的随机变量。为简化表述，我们采用多元高斯分布\(N(z;\mu_{i},\sigma_{i}^{2}I)\)的形式表示： \[p(z_{i}|x_{i})=N(z;\mu_{i},\sigma_{i}^{2}I).\]

​  其中I表示单位对角矩阵。在此公式中，μ代表表示中最可能的值，而σ2则捕捉相关概率。值得注意的是，σ2与概率呈反比关系，即σ2越大表示概率越低。μ和σ2具有相同的维度。均值μ由表示头h（·）预测。与此同时，我们引入概率头p（·）并行预测概率σ2。
​  在传统对比学习中，表征之间的相似性通常通过2距离或余弦相似度进行衡量，但这种方法无法量化两个分布之间的相似性。为解决这一问题，我们采用互似度评分（Mutual likelihood Score，简称MLS）作为衡量两个分布zi和zj之间相似性的指标，具体计算公式如下： \[\begin{aligned}M L S(z_{i},z_{j})&=\log(p(z_{i}=z_{j}))\\&=-\,\frac{1}{2}\sum_{l=1}^{D}\left(\frac{(\mu_{i}^{(l)}-\mu_{j}^{(l)})^{2}}{\sigma_{i}^{2(l)}+\sigma_{j}^{2(l)}}+\log(\sigma_{i}^{2(I)}+\sigma_{j}^{2(I)})\right)-\frac{D}{2}l o g2\pi,\end{aligned}\] ​  其中\(\mu_{i}^{(l)}\)表示\(\mu_{i}\)的第l个维度，\(\sigma_{i}^{(l)}\)同理。MLS本质上结合了加权2距离和对数正则化项。传统2距离仅考虑基于伪标签映射到潜在空间的表示之间的相似性，而未考虑其可靠性。然而，不准确的伪标签可能导致错误的优化方向并破坏潜在空间。为解决这一问题，MLS从两个角度引入zi和zj的概率来处理不准确的伪标签：  (i)在第一项中，当σ2较大时，2距离的权重会降低。这表明即使2距离显示zi和zj相似，但由于概率较低，它们之间的相似性也会减弱。通过考虑概率，MLS引入了一种衡量相似性的指标，能够反映表示的可靠性。
​  (ii)在第二项中，对数正则化惩罚低概率表示，这促使所有表示更加可靠。此外，σ2和μ可以相互作用。可学习的σ2与2距离相关联，使其能够根据表示之间的关系进行学习。反之，μ也可以通过σ2进行优化。μ和σ2之间的这种相互作用符合我们对表示学习的直觉理解。

3.3. 全球分配原型

​  在传统方法中，类别c的原型ρc通常是通过汇总当前迭代中属于类别c的所有表示的语义信息来获得的。对于概率性表示，这一过程可以表述为： \[\begin{aligned}\rho_{c}\sim N(\hat{\mu}_{c},\hat{\sigma}_{c}^{2}I),\\\frac{1}{\hat{\sigma}_{c}^{2}}=\sum_{z_{ci}\in Z_c}\frac{1}{\sigma_{ci}^{2}},\\\hat{\mu}_{c}=\sum_{z,t\in{\bf Z}_{c}}\frac{\hat{\sigma}_{c}^{2}}{\sigma_{c l}^{2}}\mu_{c i},\end{aligned}\] ​  其中\(\mathcal{Z}_{c}\)表示当前迭代中属于类别c的表征集合，即 $ Z_{c}=[z_{c0},z_{c1},,z_{c l}] $ ，而 $ z_{c i} {}N({c i},{c i}^{2}I) $ 独立同分布。尽管通过概率化表征将概率纳入表征过程中，但某些显著的误差仍会影响原型的精度，导致原型漂移现象。此外，类内方差的固有特性使得同一类别的表征在相邻迭代中产生差异，进一步加剧了原型漂移问题。为解决这些挑战，我们提出了一种从全局视角跨迭代序列化聚合表征的有效策略。具体而言，我们将当前迭代中计算出的原型定义为局部原型，并将其扩展为全局分布原型（GDP）。我们引入变量t表示训练过程中的第t次迭代，并用ρl(t)表示局部原型。为清晰起见，此处省略类别c。我们将GDP表示为ρg(t)，其数学表达式可表述为： \[p(\rho_{g}(t)|\mathcal{Z}_{g}(t))={\mathcal N}({\hat{\mu}}_{g}(t),{\hat{\sigma}}_{g}^{2}(t)I),\] ​  其中，Zg(t)表示所有观测到的相同类别表示集合，而给定Zl(t)则表示第t次迭代中相同类别表示的集合，即\({\mathcal{Z}}_{g}(t)=\mathcal{Z}_{l}(0)\cup\mathcal{Z}_{l}(1)\dots\cup\mathcal{Z}_{l}(t)\)。由于每个表示\(z_{i}\stackrel{i,i,d}{\sim}N(\mu_{i},\sigma_{i}^{2}I)\)都是独立同分布的，因此我们有 \[\begin{aligned}{\frac{1}{\hat{\sigma}_{g}^{2}(t)}}&=\sum_{z_{i}\in \mathbf{Z}_{g}(t)}{\frac{1}{\sigma_{i}^{2}}}\\&=\sum_{z_{i}\in \mathcal{Z}_{z}(t-1)}{\frac{1}{\sigma_{i}^{2}}}+\sum_{z_{i}\in \mathcal{Z}_{i}(t)}{\frac{1}{\sigma_{i}^{2}}}\\&=\frac{1}{\hat{\sigma}_{g}^{2}(t-1)}+\frac{1}{\hat{\sigma}_{l}^{2}(t)},\end{aligned}\] ​  且 \[\begin{aligned}{\hat{\mu}}_{g}(t)&=\sum_{z_{i}\in Z_{g}(t)}{\frac{\hat{\sigma}_{g}^{2}(t)}{\sigma_{i}^{2}}}\mu_{i}\\&={\hat{\sigma}}_{g}^{2}(t)\biggl(\sum_{z_{i}\in \mathcal{Z}_{g}(t-1)}{\frac{\mu_{i}}{\sigma_{i}^{2}}}+\sum_{z_{i}\in \mathcal{Z}_{l}(t)}{\frac{\mu_{i}}{\sigma_{i}^{2}}}\biggr)\\&=\hat{\sigma}_{g}^{2}(t)\biggl(\frac{1}{\hat{\sigma}_{g}^{2}(t-1)}\sum_{z_{i}\in\mathcal{Z}_{g}(t-1)}\frac{\hat{\sigma}_{g}^{2}(t-1)\mu_{i}}{\sigma_{i}^{2}}+\frac{1}{\hat{\sigma}_{l}^{2}(t)}\sum_{z_{i}\in \mathcal{Z}_{l}(t)}\frac{\hat{\sigma}_{l}^{2}(t)\mu_{i}}{\sigma_{i}^{2}}\biggr)\\&=\hat{\sigma}_{g}^{2}(t)\biggl({\frac{\hat{\mu}_{g}(t-1)}{\hat{\sigma}_{g}^{2}(t-1)}}+{\frac{\hat{\mu}_{l}(t)}{\hat{\sigma}_{l}^{2}(t)}}\biggr).\end{aligned}\]

​  这意味着我们可以从最后一个GDP \(\rho_{g}(t-1)\)和当前的本地原型\(\rho_{l}(t)\)中获得当前的GDP：

\[p(\rho_{g}|{\mathcal{Z}}_{g}(t))=p(\rho_{g}|\rho_{g}(t-1),\rho_{l}(t)),\] ​  具体来说，GDP可按如下方式更新：

\[\begin{aligned}&\rho_{g}(t)\sim{\mathcal N}({\hat{\mu}}_{g}(t),{\hat{\sigma}}_{g}^{2}(t){\cal I}),\\&\frac{1}{\hat{\sigma}_{g}^{2}(t)}=\frac{1}{\hat{\sigma}_{g}^{2}(t-1)}+\frac{1}{\hat{\sigma}_{l}^{2}(t)},\\&\hat{\mu}_{g}(t)=\hat{\sigma}_{g}^{2}(t)\biggl(\frac{\hat{\mu}_{g}(t-1)}{\hat{\sigma}_{g}^{2}(t-1)}+\frac{\hat{\mu}_{l}(t)}{\hat{\sigma}_{l}^{2}(t)}\biggr).\end{aligned}\] ​  GDP具有以下属性：

​  1.GDP考虑了所有历史表示，这些表示根据其概率σ2对GDP有所贡献。
​  2.在原型计算中，GDP \(\rho_{g}(t-1)\)等于之前迭代中的所有历史表示\(\mathcal{Z}_{g}(t-1)\)。

​  GDP的第一个特性表明，只要σ2估计得当，它就能有效抵御瞬时噪声伪标签的影响。第二个特性则说明，使用GDP进行迭代间衔接时几乎不需要额外内存开销——当前的GDP ρg(t)可以直接由上一个GDPρg（t−1）和当前局部原型ρl(t)推导得出。因此，系统无需将所有历史表征存储在内存中，只需保留最新的GDP Zg（t−1）即可。

3.4. 虚拟负样本

​  为解决负样本分布零散的问题，我们提出了一种高效策略来替代传统的记忆库方法，该策略巧妙利用了GDP的分布特性。具体而言，我们通过改进的参数重配置技术(Kingmaand & Welling 2013)，从对应类别c的GDP \(\rho_{(c)g}(t)\sim\mathcal{N}(\tilde{\mu}_{(c)g}(t),\,\hat{\sigma}_{(c)g}^{2}(t)I)\)中生成虚拟负样本（VN）：

\[{Z_{c}^{V N}=\hat{\mu}_{(c)g}(t)+\beta\epsilon^{\top}I\hat{\sigma}_{(c)g}^{2}(t),}\] ​  当\(\epsilon=(\epsilon^{(1)},\dots,\epsilon^{(d)}),\epsilon^{(1)},\dots,\epsilon^{(d)}\sim\mathcal{N}(0,1)\)时，我们定义了一个名为虚拟半径的超参数来平衡虚拟网络（VNs）的紧凑性和多样性。重参数化技巧本质上是在μ(d)为中心采样某些表示，以高斯函数N（μ(d)，σ2(d)）作为概率密度函数，并将β作为每个维度d的半径。虚拟网络继承了全局特征生成模型（GDP）的全局特征，覆盖整个迭代过程。此外，与真实表示相比，虚拟网络表现出更优的紧凑性，因为它们不受类内方差的影响。同时，虚拟网络相比全局特征生成模型具有更强的离散性。当前迭代中，小批量数据的有限规模限制了真实负样本表示仅覆盖数据集中的部分类别，导致负样本分布碎片化。然而，我们的虚拟网络的优势在于能够涵盖数据集中所有类别的表示。因此，它们不仅弥补了负样本分布碎片化的缺陷，还整合了更广泛的全局特征。

3.4.1关于记忆库的讨论

​  记忆库策略作为多项研究(Hu et al., 2021; Alonso et al., 2021;Wang et al., 2021, 2022)采用的常规解决方案，主要用于跨越迭代周期和补偿负样本分布的碎片化问题。该策略最初设计用于在有限小批量数据下扩展图像覆盖范围，但其复杂的采样机制需要频繁存取表征数据，导致计算成本显著增加（处理速度降低31%）且内存占用高达2.63GB。这是因为与实例级表征相比，像素级表征具有更高密度，每个像素（或区域）都需要映射到对应表征。为突破这些限制，我们提出一种创新策略：通过全局概率分布（GDP）和视觉网络（VN）来补充负样本分布的碎片化特征，无需依赖复杂的表征存取机制。具体而言，我们的方法仅需42KB内存即可将全局信息聚合到GDP中（对比2.63 GB)，生成视觉网络时计算成本极低（训练时间增加0.03GPU天对比0.47天）。采用此方案可在不产生记忆库策略相关巨大内存与计算开销的前提下，大规模捕获更多图像信息。

3.5. 训练目标

​  在与传统的师生框架和我们引入的组件合作的基础上，总训练对象由监督损失Ls、无监督损失Lu和对比损失Lc组成，如下所示： \[\mathcal{L}=\mathcal{L}_{s}+\mathcal{L}_{u}+\lambda_{c}(t)\mathcal{L}_{c},\] ​  其中λc(t)用于调节对比度损失的贡献，并被表述为： \[\lambda_{c}(t)=\lambda_{c0}\cdot e x p\bigg(\alpha\cdot\bigg(\frac{t}{T_{t o t a l}}\bigg)^{2}\bigg),\] ​  其中λc0表示初始缩放参数，α表示权重衰减系数，t表示当前第t个epoch，Ttotal表示总epoch数。
​  Ls通过标准交叉熵（CE）损失函数ce构建，其表达式为： \[\mathcal{L}_{s}=\frac{1}{|B_{l}|}\sum_{(x_{i}^{l},y_{i}^{l})\in B_{l}}^{}\ell_{c e}(g(f(x_{i}^{l}),y_{i}^{l})),\] ​  其中，Bl表示标记图像的批次。
​  对于Lu，我们首先设定一个阈值δu，用于统计训练集中Bu中对应置信度\(p_i^u\)高于δu的训练像素数量Nˆ。通过Nˆ和Bu中像素的总数N，Lu通过加权CE损失构建，具体公式如下： \[{\mathcal{L}}_{u}={\frac{1}{|B_{u}|}}\sum_{x_{i}^{u}\in B_{u}}\omega\ell_{c e}(g(f(x_{i}^{u}),y_{i}^{u})),\] ​  其中，\(y_i^u\)是来自教师模型的伪标签，ω是损失权重，由\(\omega={\frac{\hat{N}}{N}}\)公式化。
​  在对比损失计算过程中，考虑到GPU内存的限制，我们参考了先前的研究(Liu et al., 2022)，为对比任务采样有价值的表示。我们根据置信度π采用了一些采样策略，并在这些策略中引入了强阈值δs和弱阈值δw。我们的采样策略如下：
​  (1)有效表示采样策略我们设定δw用于采样pi值高于δw的有效表示。只有有效的表示才会被纳入对比分析。
​  (2)锚点采样策略我们设定δs用于采样对应pi值低于δs的锚点。
​  (3)负样本采样策略我们根据负类与当前锚类的GDP之间的相似性(i.e., MLS (Shi and Jain, 2019))，对不同类别的负样本进行非均匀采样。
​  我们采用InfoNCE(Van den et al., 2018)作为对比损失函数，并引入PR、GDP和VN（分别在第3.2节、3.3节和3.4节中描述），其表达式为： \[{\mathcal{L}}_{c}=-{\frac{1}{|C|\times|{\mathcal{Z}}_{c}|}}\sum_{c\in C}\sum_{z_{ci}\in{Z}_c}\log{[\frac{e^{S(z_{c i},\rho_{(c)g}(t))/\tau}}{e^{S(z_{c i},\rho_{(c)g}(t))/\tau}+\sum_{\tilde{c}\in\tilde{C}_{l}}\sum_{z_{\tilde{c}i}\in{Z}_\tilde{c}}e^{S(z_{c i},\bar{z}_{\tilde{c}j})/\tau}+\sum_{\tilde{C}\in\tilde{C}_{g}}\sum_{z_{\tilde{C}j}^{VN}\in\tilde{Z}_{\tilde{C}}^{V N}}e^{S^{(\tilde{Z}_{ci},z_{\tilde{c}J}^{N N})/\tau}}}]}\] ​  其中C表示当前迭代中所有锚点类别的集合，Zc表示属于类别c的锚点表示zi的集合，˜Cl表示当前迭代中的负类，˜Cg表示整个数据集中的负类，Zc˜表示当前迭代中真实负类表示zc j˜的集合，ZVNC˜表示属于类别c的虚拟负类表示zc j V N˜的集合，ρ（c˜）g(t)表示当前属于类别c的GDP，τ表示温度参数，s为MLS。由于修改后的重参数化技巧中概率可能缺失，我们通过经验方式对虚拟负类的概率进行零填充处理。
​  在训练概率头时，我们采用了名为“软冻结”的策略，该方法参考了文献[1]。具体来说，我们将概率头的训练与主干网络及分割头的训练分开进行，并为其设置较小的学习率。采用这种策略是为了确保训练过程的稳定性。由于初始阶段的概率头输出会因表示不合理而急剧上升，因此必须为其设置远低于主干网络的学习率，以确保其训练进度与其他模块同步，并促进网络各组件间的协同工作。我们的框架如图3所示，同时训练过程详见算法1。

---

算法1类似PyTorch的训练过程伪代码

---

网络结构：学生编码器：f，学生分割头：g，教师编码器：f，教师分割头：g，表示头：h，概率头：p
输入：由\((X^{l},\,Y^{l})\)和\((X^{u})\)组成的小批量B，最后一层的GDP \(\rho_{g}(t-1)\)。
注释：锚类c，保留当前迭代中类别\(\tilde{C_l}\)，保留数据集中类别\(\tilde{C_g}\)

---

1. for epoch in range(total_epoch) do
   2. ​ \(P^{l}=g(f(X^{l}))\) #在带标签的图像上进行预测
   3. ​ \(\mathcal{L}_{s}=ce\_l o s s(P^{l},Y^{l})\) #计算监督损失Ls
   4. ​ \(Y^{u}\ =m a x\_o p(g^{\prime}(f^{\prime}(X^{u})))\) #通过公式1中的最大值运算生成伪标签，公式1：\(y_{i}^{u}=\mathbf{1}_{c}(\arg\operatorname*{max}_c\{p_{i,c}^{u}\}_{c\in C})\)
   5. ​ \(P^{u}=g(f(X^{u}))\) #在未标记的图像上进行预测
   6. ​ \(\mathcal{L}_{u}=ce\_l o s s(P^{u},Y^{u})\) #计算监督损失Lu
   7. ​ \((X,Y)\leftarrow c o m b i n e((X^{I},Y^{I}),(X^{u},Y^{u}))\) #将标记和未标记的训练集合并
   8. ​ for (X,Y) ∈ B do
   9. ​ \(\mathcal{L}_{c}=0\) #初始化Lc
   10. ​ \(\mu=h(f(X))\) #计算μ
   11. ​ \(\sigma^{2}=p(f(X))\) #计算σ2
   12. ​ \(Z\leftarrow(\mu,\sigma^{2})\) # 由μ和σ2组成的表示
   13. ​ \(Z_{v a l},Y_{v a l},C_{v a l}\leftarrow m a s k(Z,Y)\) # 根据抽样策略，δw的掩膜
   14. ​ for c ∈ Cval do
   15. ​ \(\rho_{l}^{c}(t)\,\leftarrow\,c a l c u l a t e_{-}p r t(Z_{v a l}^{c})\) # 通过公式4计算局部原型
   16. ​ \(\rho_{g}^{c}(t)\leftarrow u p d a t e_{-}p r t(\rho_{g}^{c}(t-1),\rho_{l}^{c}(t))\) # 通过公式9更新GDP
   17. ​end for
   18. ​ for c ∈ Cval do
   19. ​ \(\mathcal{L}=0\) # 初始化当前类中的损失L
   20. ​ \(Z_{a}^{c}\leftarrow s a m p l e_{-}a(Z_{v a l}^{c},Y_{v a l}^{c})\) # 采样锚点表示
   21. ​ \(n e g_{-}d i s t\ \sim\,[M L S(\rho_{g}^{c}(t),\,\rho_{g}^{\tilde{c}_l}(t))\ f o r\ \tilde{c}_{l}\;i n\;\tilde{C}_{l}]\) # 计算负采样分布
   22. ​ \(Z_{n}\leftarrow s a m p l e_{-}n(Z_{v a l}^{\tilde{c}_{l}},n e g_{-}d i s t)\) # 采样真实负样本表示
   23. ​ \(Z_{V N}\leftarrow [g e n e r a t e_{-}VN(\rho_{g}^{\tilde{C}_{g}}(t)){f o r}\ \tilde{c}_{g}\ in\ \tilde{C}_{g}]\) # 使用公式10生成虚拟负值，公式10：\({Z_{c}^{V N}=\hat{\mu}_{(c)g}(t)+\beta\epsilon^{\top}I\hat{\sigma}_{(c)g}^{2}(t),}\)
   24. ​\(\mathcal{L}=c o n t r a s t_{-}^{\phantom{c c c}}l o s s(Z_{a}^{c},Z_{n}^{\phantom{c}},Z_{n},Z_{V N}^{\phantom{c}},\rho_{g}^{c}(t))\) # 使用公式15计算Lc
   25. ​ \(\mathcal{L}_{c}=\mathcal{L}_{c}+\mathcal{L}\)
   26. ​end for
   27. ​ end for
   28. ​ \(\mathcal{L}_{t o t a l}=\mathcal{L}_{s}+\mathcal{L}_{u}+\lambda\mathcal{L}_{c}\) # 计算总损失Ltotal，λ是方程11中λc(t)的当前值。
   29. ​ optimizer.zero_grad()
   30. ​ \(\mathcal{L}_{t o t a l}\).total.backward()
   31. optimizer.step()
   32. end for

---

问题：最近的半监督语义分割（S4）方法通过将对比学习引入师生培训范式，取得了长足的进步。然而，这些方法存在两个关键局限性：

• 它们对用于监督未标记图像对比学习的不准确伪标签缺乏鲁棒性。
• 用于收集表示的原型（类质心）在训练迭代中发生了变化。此外，由于小批量大小有限，负表示的分布在每次迭代中都是分散的。

提出的解决方案：为了解决第一个问题，本文提出使用多元高斯分布将像素级表示建模为概率表示（PR）。PR包含一个捕获最可能表示的均值向量和一个表示可靠性的方差向量。PR之间的相似性是通过相互似然评分来衡量的，该评分减少了不确定表示的影响。

对于第二个问题，引入了全球分布原型（GDP），以在整个训练过程中聚合全球表示，确保原型位置的一致性。此外，虚拟负片可以从GDP中有效地生成，以补偿零碎的负分布，而不需要内存库。

主要贡献：

• 引入概率表示的概念，以提高S4对比学习中对不准确伪标签的鲁棒性。
• 提出全球分布原型和更新策略，以保持训练迭代中原型的一致性。
• 从GDP生成虚拟负数，以缓解零碎的负数分布问题，同时高效。
• 在PASCAL VOC和Cityscapes数据集上实现了优于最先进方法的卓越性能。消融研究验证了每个拟议组件的有效性。

​  本文提出了一种用于半监督语义分割的鲁棒对比学习框架，该框架将像素表示建模为概率分布，在迭代中构建全局原型，并为增强的潜在空间生成虚拟否定。