Pixel-Level Anomaly Detection via Uncertainty-aware Prototypical Transformer
Pixel-Level Anomaly Detection via Uncertainty-aware Prototypical Transformer
Chao Huang, Chengliang Liu, Zheng Zhang, Zhihao Wu, Jie Wen, Qiuping
Jiang, Yong Xu
1 中国黑龙江省哈尔滨市哈尔滨工业大学
2
宁波大学
摘要
像素级视觉异常检测旨在从图像中识别异常区域,在工业故障检测和医学诊断领域具有重要作用。
然而,由于以下原因,该任务具有挑战性:
i)
异常区域存在显著差异;
ii)
异常区域与正常环境的边界模糊不清。
本研究提出了一种不确定性感知原型transformer(UPformer,uncertainty-aware
prototypical
transformer),该模型同时考虑异常区域的多样性和不确定性,从而实现精准的像素级视觉异常检测。为此,我们首先设计了记忆引导的原型学习变换器编码器,通过学习并记忆异常区域的原型表示,使模型能够捕捉异常区域的多样性特征。此外,我们设计了一种异常检测不确定性量化器,用于学习异常检测的分布特征以量化检测不确定性。同时,提出了一种不确定性感知变压器解码器,通过利用检测不确定性引导模型聚焦不确定区域,从而生成最终检测结果。通过结合原型学习与不确定性估计的优势,我们的方法实现了更精准的异常检测。在五个数据集上的实验结果表明,该方法达到了当前最先进的异常检测性能。
1 引言
视觉异常检测(VAD)[15-17,42]是计算机视觉领域的基础任务。由于其在工业故障检测、医学图像分析等领域的广泛应用潜力,该技术已引发广泛关注。图像级
VAD
[26,39]旨在区分正常与异常图像中的异常特征,而像素级异常检测(PAD)[21,32,38,41]则专注于识别异常图像中的异常像素。实际上,像素级检测高度依赖人工经验与专业能力,因此亟需开发自动化方法来替代技术门槛较高的传统人工检测。
尽管像素级检测已取得显著进展,但其挑战性仍源于两个关键因素:首先,异常特征通常具有较大的类内方差(即在尺寸、形状、纹理、颜色等方面存在显著差异),往往缺乏区域性的明显特征模式;其次,异常特征与正常环境的边界通常模糊不清,且缺乏异常检测所需的高类间方差。因此,优秀的异常检测模型需要有效捕捉这两个核心特征。
早期方法[1,27,35]主要依赖人工设计的特征,通过训练分类器来区分异常与正常区域,但由于人工特征的表征能力有限,这些方法往往难以获得理想效果。随着深度学习技术的突飞猛进,基于深度神经网络的方法取得了重大突破。特别是采用跳跃连接编码器-解码器结构的U型网络[11,19,33,46,49],相比早期方法性能有了显著提升。但这些方法仅关注异常区域的整体特征,却忽视了对病变检测至关重要的模糊边界问题。为此,多项研究[12,31]通过在异常检测模型中引入边界信息来提升性能,不过在兼顾同一语义类别表征一致性方面,相关研究仍较为匮乏。
在本文中,我们设计了一种新型的不确定性感知原型变换器(UPformer,uncertainty-aware
prototypical
transformer),该模型将记忆增强模块与贝叶斯神经网络(BNN)整合到异常检测框架中。与现有研究不同,我们的UPformer通过结合原型学习与不确定性估计的优势来推断异常。其设计动机如下:
i)
我们认为,使模型能够为同类异常生成语义一致的表征,可有效解决像素级异常检测中异常多样性带来的问题;
ii)
我们还认为图像异常识别本身具有不确定性特征,利用这种检测不确定性来增强模型性能具有显著优势。
因此,我们的模型旨在捕捉异常的多样性和不确定性特征。为此,我们首先学习并记忆各类异常的原型表征,随后将输入图像提取的特征通过这些记忆的原型表征进行表征,从而使模型能够为同一类异常生成语义一致的表征。此外,我们利用
BNN
生成每个像素点异常检测结果的概率分布,并估计每个像素点的异常检测不确定性。同时,我们借助异常原型和检测不确定性,通过Transformer推断异常。因此,视觉异常检测任务被转化为原型与不确定性引导的异常检测图生成任务。
具体而言,UPformer主要包含三个核心模块:i)
异常检测不确定性量化器(AUQ)、ii)
内存引导原型变换器编码器(MPE)以及iii)
不确定性感知变换器解码器(UAD)。首先, AUQ
旨在学习概率分布而非单一固定像素估计值。随后,从该分布中抽取 𝑁
样本以计算检测不确定性。通过这种方式,我们的 AUQ
使模型能够利用额外的统计信息进行异常检测。接着, UAD
利用异常检测不确定性获取不确定性感知表征,从而提升模型在不确定区域的异常检测精度。此外,MPE的设计通过确保相同异常的表征一致性,鼓励
UAD 捕捉异常的多样性特征。
本研究的主要贡献如下:
- 我们开发了一种新型原型与不确定性引导的视觉异常检测框架,该框架将不确定性估计和原型学习嵌入Transformer中,以捕捉异常的多样性和不确定性。因此,该模型能够利用多重检测的额外统计信息对异常进行推理。
- 我们设计了一种记忆引导的原型变换器编码器,用于学习并记忆异常的原型表示,从而使模型能够为同类异常生成语义一致的表征,并有效解决异常多样性带来的问题。
- 我们设计了一种异常检测不确定性量化器,用于学习检测结果的分布,以量化每个像素的异常检测不确定性。
- 我们采用一种不确定性感知的Transformer解码器,在异常原型和检测不确定性的辅助下,更准确地识别异常。
2 相关工作
2.1 视觉异常检测
像素级异常检测(PAD,pixel-level anomaly detection)通常被定义为异常区域分割任务,旨在从图像中识别异常区域,具有广泛的应用前景。早期研究[1,27,35]主要依赖纹理、颜色、形状、外观等低级特征或混合特征,但由于这些特征的表征能力有限,往往难以取得理想效果。随着深度学习技术的突破[5–8,24,25,45,47],基于深度神经网络的方法取得了重大进展。例如U型结构网络(如U-Net[33]、U-Net++[49])通过利用多层级特征生成高分辨率检测结果,显著提升了性能。此外,部分研究[12,31]通过在模型中引入边界信息来增强检测效果。相比之下,我们的方法无需任何额外信息即可实现更精准的异常检测。
2.2 不确定性估计
当前,不确定性估计已广泛应用于各类计算机视觉任务,包括伪装目标检测[40]、语义分割[18]、显著性检测[43]及医学图像分析[23]。贝叶斯神经网络通常通过学习神经网络权重的概率分布来量化不确定性。受这些研究启发,我们构建了一个基于 BNN 的异常检测不确定性量化器(AUQ),用于估计PAD中的不确定性,从而增强模型的鲁棒性。
2.3 视觉Transformer
Transformer [36] 近年来在计算机视觉领域引发广泛关注,这得益于其在序列建模方面的卓越能力。在图像识别 [22]、语义分割 [48] 和目标检测 [40] 等任务中,其性能表现与基于卷积神经网络(CNN)的模型不相上下甚至更胜一筹。例如,Kolesnikov等人 [22] 将图像转换为图像块序列,并将这些块输入Transformer以实现高效图像分类。Yang等人 [40] 将伪装目标检测建模为推理任务,构建了两个Transformer来处理该任务。Zheng等人 [48] 则采用Transformer解决语义分割中的上下文推理问题。此外,多项研究 [2,13,40] 证实掩码机制能有效引导模型聚焦于被遮蔽内容,显著提升模型的推理能力。受这些方法启发,本研究设计了一种用于目标检测的Transformer。具体而言,记忆引导原型编码器(MPE,memory-guided prototype encoder)通过学习并存储异常样本的原型表示来确保表征一致性,而不确定性感知解码器 (UAD ,uncertainty-aware decoder)则尝试结合不确定性与原型信息进行异常推理。
3 方法
本文提出的像素级异常检测(PAD)旨在区分图像中每个像素的正常与异常状态。我们将PAD建模为异常检测图生成任务:给定包含
D数据对\(\{X_i,Y_i\}\)的训练集\(D=\{X_i,Y_i\}^D_{i=1}\),其中\(X_{i}\in\mathbb{Z}^{H\times
W\times3}\)表示输入图像,\(Y_{i}\in\mathbb{Z}^{H\times
W\times1}\)表示其真实值。目标是学习一个异常检测模型\(S_{\Phi}:X\to\mathbf{A}\),该模型能从图像X生成异常检测图\(A\in\mathbb{Z}^{H\times
W\times1}\)。对于A中的每个像素 𝑗 ,异常分数 𝑎𝑗
∈[0,1]即为模型的检测结果,其中0和1分别表示该像素为正常和异常状态。
具体而言,我们设计了一种新型的不确定性感知原型变换器(UPformer),该模型将记忆增强模块与贝叶斯神经网络(BNN)整合到异常检测系统中。与现有研究不同,我们的UPformer通过结合原型学习与不确定性估计的优势来推断异常,如图1所示。
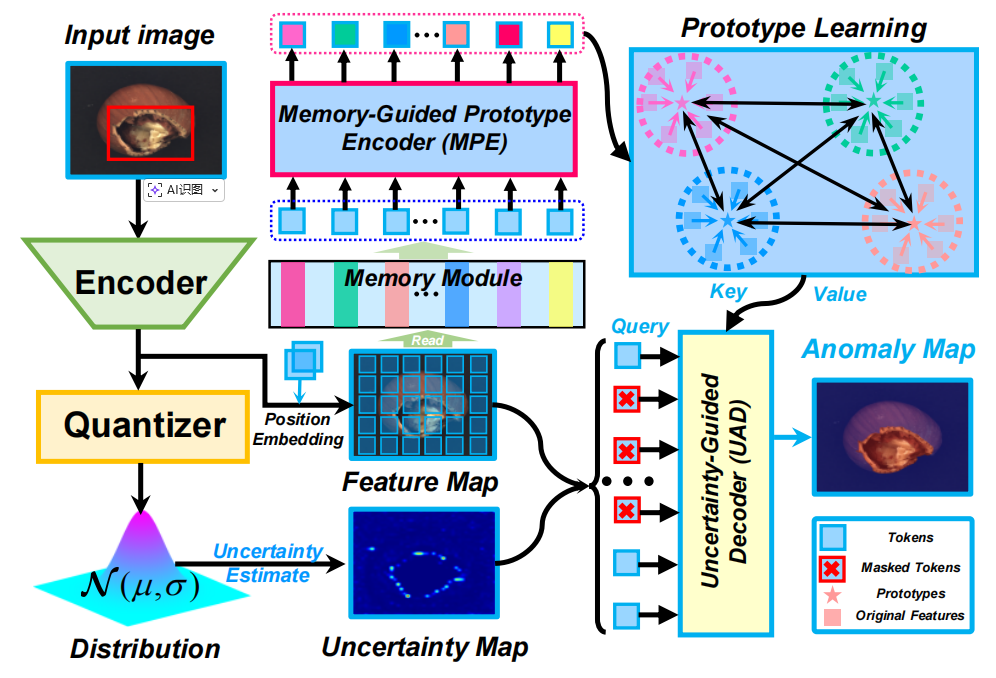
图1:我们的模型包含三个主要部分:异常检测不确定性量化器(AUQ)、记忆引导原型编码器(MPE)和不确定性感知解码器(UAD)。 AUQ 学习并估计检测的不确定性。MPE旨在学习并存储异常的原型表示。 UAD 利用不确定性与原型实现精准的异常检测。
具体而言,UPformer主要包含三个部分:
1)异常检测不确定性量化器AUQ ,由编码器\(Q_{\beta1}\)和量化器\(Q_{\beta2}\)两部分组成。其中,编码器\(Q_{\beta1}\)从输入图像\(X\in\mathbb{Z}^{H\times
W\times3}\)中提取特征\(\mathbf{F}\in\mathbb{Z}^{h\times w\times
c}\),而量化器\(Q_{\beta2}\)则通过测量异常检测分布的方差来估计每个像素的不确定性。在实际应用中,我们首先将每个像素的检测结果分布建模为均值
𝝁 、方差 𝝈 的高斯分布,然后从该分布中抽取样本以生成不确定性图M。
2)记忆引导原型编码器MPE模块,通过学习并记忆异常的原型表征,使模型能够确保同类异常的表征一致性。本文中,
𝐾个原型\(\mathbf{P}=\{p_{1},...,p_{K}\}\in\mathbb{Z}^{K\times
c}\)通过Transformer中的注意力机制从特征F中学习得到。我们预期这些学习到的原型能帮助模型克服异常多样性带来的挑战。
3)不确定性感知解码器UAD,模块利用已学习的F、M和P生成精炼的判别特征\(\mathbf{Z}\in\mathbb{Z}^{h\times w\times
c}\),即 \({\mathcal{U}}_{\phi}:(\mathbf{F},\mathbf{M},\mathbf{P})\to\mathbf{Z}\)。最后采用解码器\({\mathcal{D}}_{\psi}\)将学习到的特征Z映射为最终的异常检测图A,即\({\mathcal{D}}_{\psi}:Z\to\mathbf{A}\)。
3.1 异常检测不确定度量化器
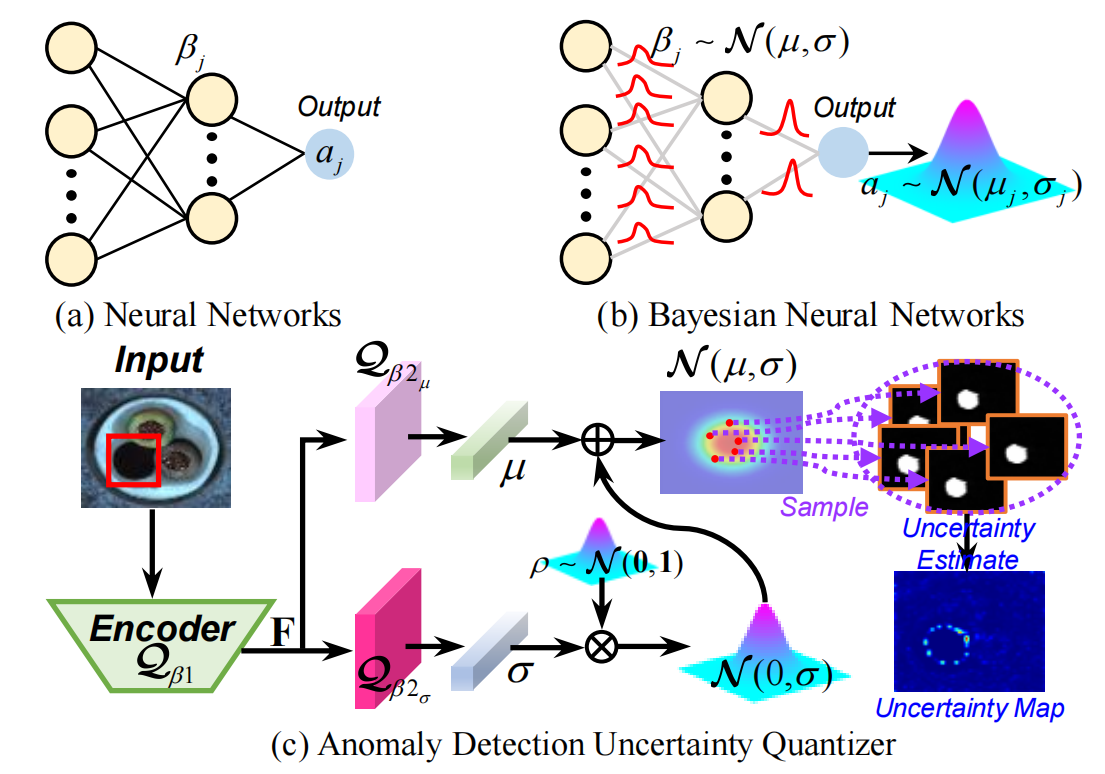
图2:与(a)神经网络相比,(b)双向神经网络的网络参数采用高斯分布采样,从而能够估计不确定性。(c)异常检测不确定性量化器由编码器 Q𝛽1 和量化器 Q𝛽2 组成,其中\(Q_{\beta1}\)从X中提取特征F,\(Q_{\beta2}\)估计异常检测的不确定性。
要判断像素是否属于正常或异常区域,最直观的解决方案是采用神经网络(NNs)构建异常检测模型,如图2(a)所示。但神经网络的输出仅是点估计值,难以准确识别存在不确定性的区域。此外,当模型出现过拟合问题时,基于神经网络的异常检测器在错误检测结果中容易产生过度自信。为此,我们在模型中引入双向神经网络(BNNs)以更精准识别不确定异常区域,如图2(b)所示。通过引入双向神经网络,我们的模型能够获取每个像素的检测不确定性。这种检测不确定性可用于引导模型更加关注不确定区域,从而提升检测效果。
为此,我们设计了
AUQ \(Q_{\beta}\)来获取检测不确定性,该
Q𝛽 由两部分组成:编码器 \(Q_{\beta1}\)
和量化器 \(Q_{\beta2}\)
,如图2(c)所示。前者用于提取特征\(F=Q_{\beta1}(\mathbf{X})\),后者则量化检测不确定性M。
AUQ 不预测单一固定点估计,而是为每个像素 𝑗
学习检测结果的概率分布。根据文献[20,40]的研究,该分布被建模为高斯分布。具体而言,AUQ算法为像素j生成的异常分数
\(a_j\) 服从高斯分布,即 $
a_{j}{N}({j},,{j})$ 。均值 \(\mu_{j}\in\mathbb{Z}^{h\times w\times1}\)
和方差\(\sigma_{j}\ \in\ \mathbb{Z}^{h\times
w\times1}\)由量化器\(Q_{\beta2}\)
生成。如文献[20]所述,随机采样会阻碍误差反向传播。为此,我们引入服从标准高斯分布\(\rho_{j}\sim {\mathcal N}(0,1)\)的变量\(\rho_{j}\)来生成采样点。通过计算\(\mu_{j}+\rho_{j}\sigma_{j}\)来获取样本,使梯度能够反向传播以优化
\(Q_{\beta}\)网络参数。异常检测映射\(\mathbf{A}_{s a m
p}=\{a_{n}\}_{1}^{N}\)从学习到的分布中采样,用于计算每个像素的不确定性。文献[20,40]指出,\(\mathbf{A}_{s a m
p}\)的方差可视为检测不确定性\(\mathbf{M}\in\mathbb{Z}^{h\times
w\times1}\)。损失函数是: \[\mathcal{L}_{Q}=-\left[\mathbf{Y}\cdot\log(a_{n})+(1-\mathbf{Y})\cdot\log(1-a_{n})\right]+\lambda\cdot
D_{K L}({\cal N}(\mu,\sigma)||{\cal N}(0,1)),\] 其中 \(a_{n}\)
是从学习到的概率分布中抽取的样本;Y是真实值; 𝜆 =0.1是加权因子。 \(\mu\in\mathbb{Z}^{h\times w\times1}\) 和
\(\sigma\ \in\ \mathbb{Z}^{h\times
w\times1}\)分别表示从量化器 \(Q_{\beta2}\) 计算得到的均值图和方差图。
3.2 基于记忆的原型编码器
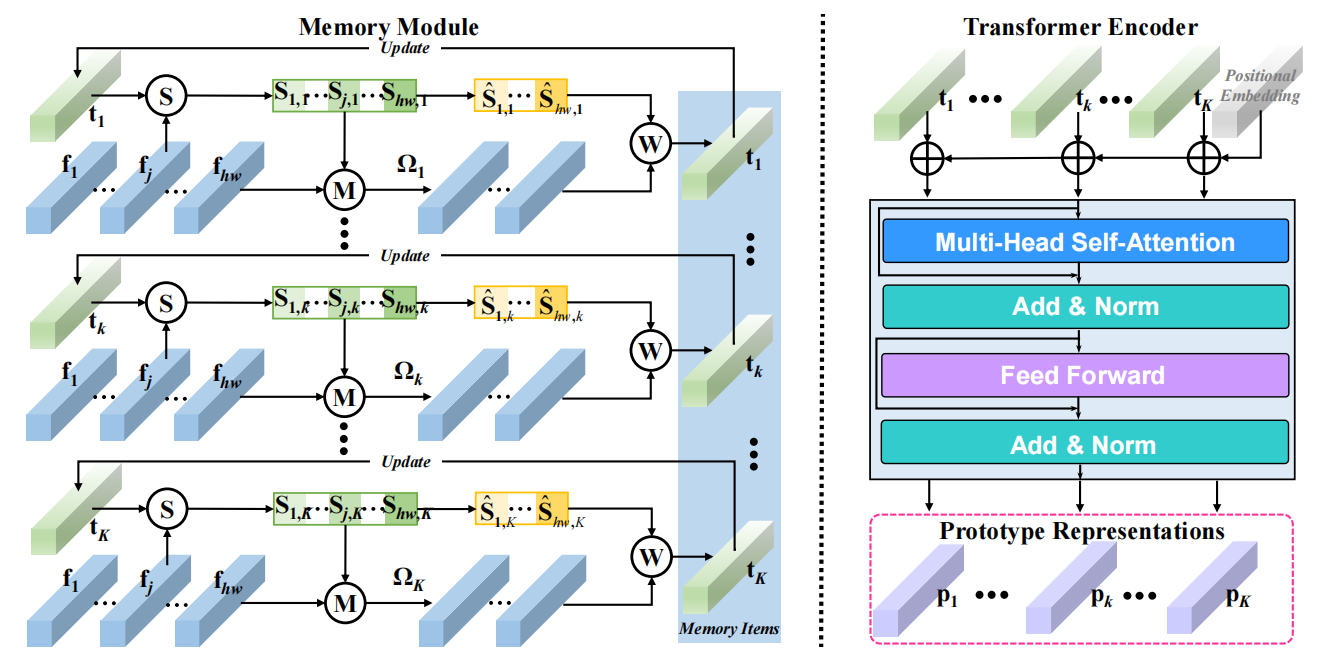
图3:我们的MPE包含两个组件:记忆库和Transformer编码器。为获取记忆项,我们首先计算记忆项 \(t_k\) 与局部特征 \(\{\mathbf f_j\}_1^{hw}\) 之间的相似度 \(S_{j,k}\) 。随后,我们计算局部特征集合 \(\Omega_{k}\) 中各特征与对应相似度的加权平均值,并将其添加到初始项 \(t_k\) 。最后,通过Transformer编码器对记忆项进行优化,最终获得原型 \(\mathbf{P}=\{\mathbf{p}_{k}\}_{1}^{K}\) 。
为应对异常多样性带来的挑战,我们通过将原型学习与Transformer结合构建MPE(记为
\({\mathcal{P}}_{\theta}\)),该模型从特征F中学习原型表示\(\mathbf{P}=\{p_{1},...,p_{K}\}\in\mathbb{Z}^{K\times
c}\)并将其存储于记忆库中(如图3所示)。通过这种方式,新输入可通过Transformer框架表示为存储原型的加权和。得益于学习到的异常原型,我们的模型能够为同类型异常生成语义一致的表示。
输入特征
\(\mathbf{F}\in\mathbb{Z}^{h\times w\times
c}\) 首先被重构为一组局部特征,即 \(\mathbf{F}=\{\mathbf{f}_{j}\}_{1}^{h w}\)
,其中 \(\mathbf{f}_{j}\in\mathbb{Z}^{c}\)
。实际操作中,原型由记忆库中的可学习记忆项组 \(\mathbf{T}=\{\mathbf{t}_{k}\}_{1}^{K}\)
生成。为获取最优记忆项\(\mathbf
T\),我们首先计算\(\mathbf
T\)与\(\mathbf
F\)之间的相似度矩阵\(\mathbf
S\)。 \[S_{j,k}={\frac{\exp(d((\mathrm{t}_{k})^{\top},\mathrm{f}_{j}))}{\sum_{j=1}^{h_{W}}\exp(d((\mathrm{t}_{k})^{\top},\mathrm{f}_{j}))}},\]
其中 \(\exp(\cdot)/\sum\exp(\cdot)\)
为softmax函数, \(d(\cdot,\cdot)\)表示余弦相似度。 \(\mathbf{f}_{j}\in\mathbf{F}\)表示第 𝑗
个局部特征, \(\mathbf{t}_{k}\in\mathbf{T}\) 表示第 𝑘
个记忆项。在记忆库参数更新时,我们使用所有查询局部特征中最近记忆项为
\(\mathbf{t}_{k}\) 的特征来更新记忆项
\(\mathbf{t}_{k}\) 。用 \(\Omega_{k}\) 表示 \(\mathbf{t}_{k}\)
对应的局部特征集合。我们利用该集合 \(\Omega_{k}\)
索引的局部特征对相似度矩阵\(\mathbf
S\)进行归一化处理 \[\widehat{S}_{j,k}={\frac{\mathrm{S}_{j,k}}{\operatorname*{max}_{j^{\prime}\in\Omega_{k}}\mathrm{S}_{j^{\prime},k}}}.\]
随后,我们利用记忆更新矩阵 \(\widehat{S}\) 和输入特征\(\mathbf F\)按以下方式更新每个原型 \[\mathbf{t}_{k}\leftarrow \mathcal
N(\mathbf{t}_{k}+\sum_{j\in\Omega_{k}}{\widehat{\mathbf{S}}}_{j,k}\cdot{\hat{\mathbf{f}}}_{j}).\]
通过上述操作,我们可获得记忆项\(\mathbf
T\)。与文献[26,29]类似,我们采用两种记忆学习损失函数,即记忆紧凑性损失和记忆多样性损失。具体而言,记忆紧凑性损失用于缩小输入特征向量与其最相关记忆项之间的差异
\[{\mathcal L}_{C}=\frac{1}{h w}\sum_{j=1}^{h
w}||{\mathbf f}_{j}-\mathrm{t}_{k}^{*}||_{2},\]
其中∗表示输入局部特征 \(\mathbf
f_{j}\) 中最相关的记忆项索引,即\(*\
=\arg\operatorname*{max}_{k\in[1,K]}\mathbf{S}_{j,k}\)。为获取多样化记忆项目而采用的记忆多样性损失
\[\mathcal{L}_{M}=\sum_{j=1}^{h w}[||{\mathbf
f}_{j}-\mathbf{t}_{k}^{*}||_{2}-||{\mathbf
f}_{j}-\mathbf{t}_{k}^{\dagger}+\gamma||_{2}]_{+},\] 其中\(\dagger\)表示输入局部特征 \({\mathbf f}_{j}\) 的第二重要记忆项索引,即
\(\dagger=\arg\operatorname*{max}_{k\in[1,K],k\neq*}\mathbf{S}_{j,k}.\gamma\)
表示记忆项之间的间隔。最后,通过transformer模块对记忆项进行优化,以获得最终原型
\[\begin{array}{l}Q=\mathbf{T}_{l n}^{l}\cdot
W_{Q},K=\mathbf{T}_{l n}^{l}\cdot W_{K},V=\mathbf{T}_{l n}^{l}\cdot
W_{V},\\{\widehat{\mathbf{T}}}^{l+1}=s o f t m a x(Q
K^{\mathsf{T}}/\sqrt{c})V+\Gamma^{l},\\\mathbf{T}^{l+1}=L a y e r N o r
m(f c(\tilde{\Gamma}_{l
n}^{l+1})+\tilde{\Gamma}^{l+1}),\end{array}\] 其中\(\mathbf{T}^{l}\)是第l层的输入记忆项。Q、K和V分别表示查询、键和值。\(W_Q\)、\(W_K\)和\(W_V\)是可学习参数。\(l_n\)表示归一化张量。\(s o f t m a x(\cdot)\)和\(f
c(\cdot)\)分别表示softmax函数和全连接层。这里我们暂不讨论多头自注意力机制的公式[36],因为目前该机制已非常普遍。最后,MPE生成的原型表示\(\mathbf{P}\in\mathbb{Z}^{K\times
c}\)旨在捕捉不同类型异常的语义特征。根据文献[26,29,40],我们定义了原型多样性损失以确保学习到的原型具有多样性。
\[\mathcal{L}_{P}=\sum_{\mathbf
p_{i}}\operatorname*{max}(0,m-||{\mathbf{p}}_{i},\mathbf{p}_{j}||_{2}^{2}),\]
其中 𝑚 为超参数。因此,MPE的原型判别损失函数为\(\mathcal{L}_D=\mathcal{L}_C+\mathcal{L}_M+\mathcal{L}_P\)。
3.3 不确定性感知解码器
为引导模型捕捉异常多样性并聚焦不确定区域,我们设计了不确定性感知异常解码器(UAD)\(\mathcal{U}_{\phi}\) ,该模型利用特征\(\mathbf F\)、不确定性\(\mathbf M\)和原型\(\mathbf P\)生成增强特征\(\mathbf Z\),用于解码最终异常检测图\(\mathbf A\),即\({\mathcal U}_{\phi}:({\mathrm F,M},{\mathrm P})\rightarrow{\mathrm Z}\)。 UAD 采用标准Transformer架构,将原始特征\(\mathbf F\)转换为判别特征\(\mathbf Z\)以实现鲁棒异常检测。在 UAD 中,多头交叉注意力机制通过不确定性感知特征 \(\mathbf F_{UA}\) 计算查询,并利用原型\(\mathbf P\)生成键值对。 \[\begin{array}{l}\widehat{Q_{h}}=\mathrm{F}_{U A}\cdot W^{\widehat{Q_{h}}},\widehat{K_{h}}=\mathrm{P}\cdot W^{\widehat{K_{h}}},\widehat{V_{h}}=\mathrm{P}\cdot W^{\widehat{V_{h}}},\\H e a d_{h}=A t t e n t i o n(\widehat{Q_{h}},\widehat{K_{h}},\widehat{V_{h}}),\\M H(Q,K,V)=H e a d_{1}\textcopyright H e a d_{2},...,\textcopyright H e a d_{H},\end{array}\] 其中\(W^{\widehat{Q_{h}}}\) , \(W^{\widehat{K_{h}}}\) 和 \(W^{\widehat{V_{h}}}\) 表示第 ℎ 个头部的项目层参数。\(\textcopyright\)表示拼接操作。通过交叉注意力操作,不同异常的语义信息和检测不确定性可被整合到最终精炼特征Z中,这有助于模型应对异常多样性和不确定性的挑战。最终,判别特征Z输入解码器生成最终异常检测图A。模型的总体训练损失可表示为\(\mathcal{L}=\mathcal{L}_{Q}+\mathcal{L}_{D}+\mathcal{L}_{B C E}(\mathbf{A},{\bf Y})\)。
4 实验
4.1 实验设置
数据集
本研究采用五个公开数据集进行性能评估。MVTecAD[3]是工业异常检测领域的大型数据集,包含15类共1258张异常图像。针对该数据集,我们随机选取977张图像用于训练,281张用于测试。值得注意的是,训练集和测试集均包含全部15类异常图像。ClinicDB[4]、ColonDB[35]、Endoscene[37]和
ETIS
[34]是医学影像异常检测的四大基准数据集。针对这些数据集,我们遵循文献[11]中的实验设置。
评价指标
本文采用四种常用评估指标:加权F值(加权平均
𝛽
𝜔)[28]、S值(𝑆𝛼)[9]、平均E值(平均绝对误差)[10]以及平均绝对误差(MAE)。
实施细节
编码器采用ResNet[14]架构。MPE由8层6头Transformer编码器构成,
UAD
则采用8层6头Transformer解码器,并在各Transformer层中加入多头交叉注意力层。我们对模型组件(AUQ
、MPE和 UAD)进行随机初始化。模型基于Pytorch[30]框架在Nvidia GTX 3090
GPU上运行,采用学习率 𝑒
−6的随机梯度下降法进行优化。训练阶段设置批量大小为8。
比较方法
我们将本方法与五种开源 SOTA
方法进行对比:U-Net[33]、U-Net++[49]、SFA[12]、ACS[44]和PraNet[11]。为确保公平性,我们采用这些模型的源代码来评估其异常检测性能。
4.2 定量结果
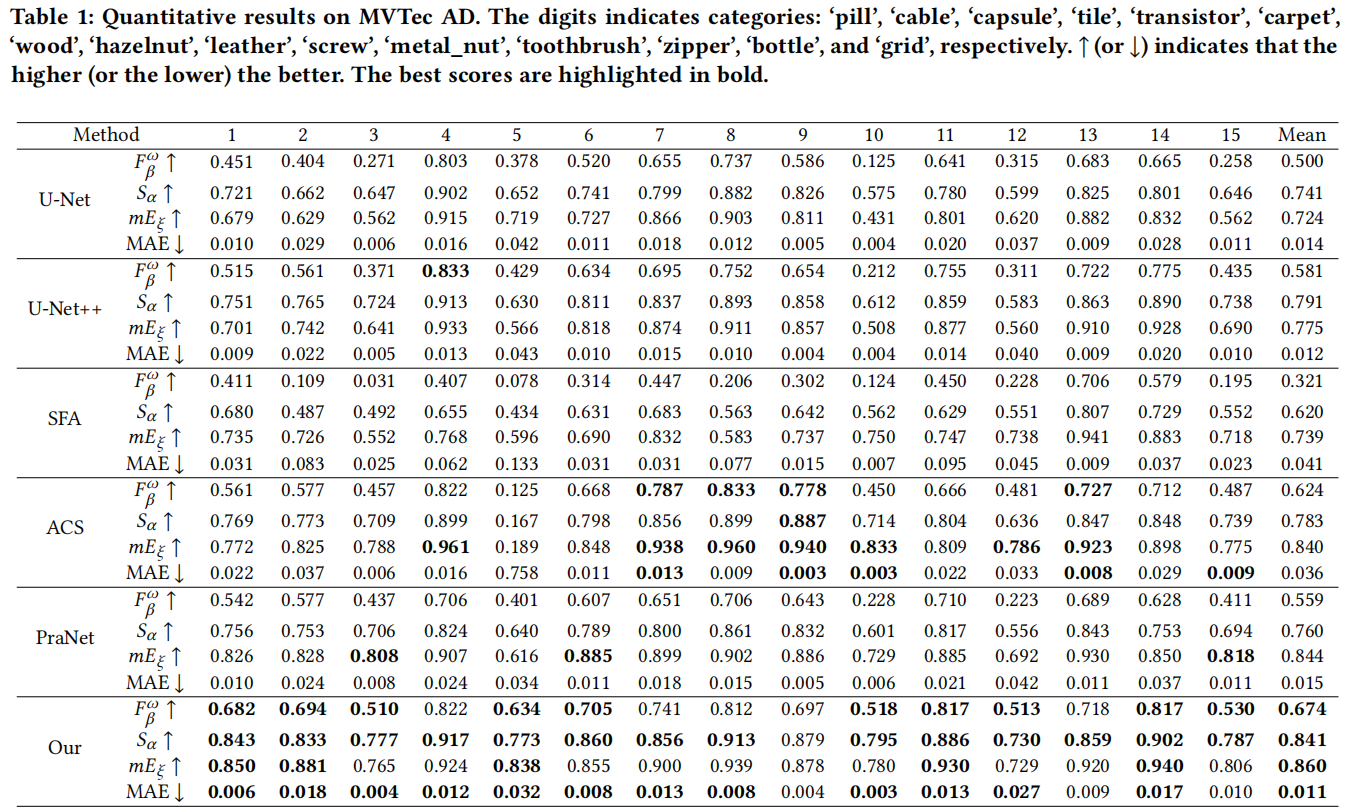
我们在工业缺陷检测数据集(MVTecAD)和医学图像异常检测数据集(ClinicDB[4]、ColonDB[35]、Endoscene[37]和 ETIS [34])上,将UPformer与五种 SOTA 方法进行对比。具体对比结果分别列于表1和表2。
工业图像数据集测试结果
如表1所示,我们的UPformer在MVTec
AD数据集上表现最佳,四项指标均取得最优成绩。具体而言,其平均 𝐹 𝛽 𝜔
达到0.674,较 SOTA ACS[44]高出5.0%。在 𝑆𝛼 方面,我们的方法比 SOTA
ACS[44]提升了5.8%。UPformer的 𝑚𝐸𝜉 值为0.860,较PraNet[11]报告的 SOTA
表现0.844高出1.6%。此外,UPformer的MAE值为0.011,优于 SOTA
U-Net++[49]。这些性能提升充分验证了UPformer的有效性和优越性。
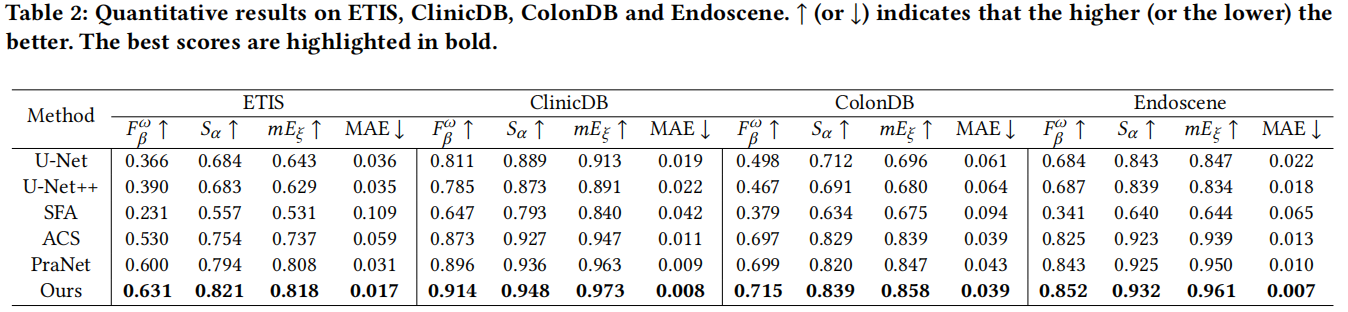
医学图像数据集上的表现
如表2所示,UPformer在所有医学图像数据集上均取得优于所有对比模型的性能提升,充分证明了本方法的优越性。与
SOTA PraNet[11]相比,UPformer在 \(F_{\beta}^{\omega}\) 、 \(S_{\alpha}\) 和 \(m E_{\xi}\)
上分别实现了1.85%、1.63%和1.05%的平均提升。
4.3 定性结果
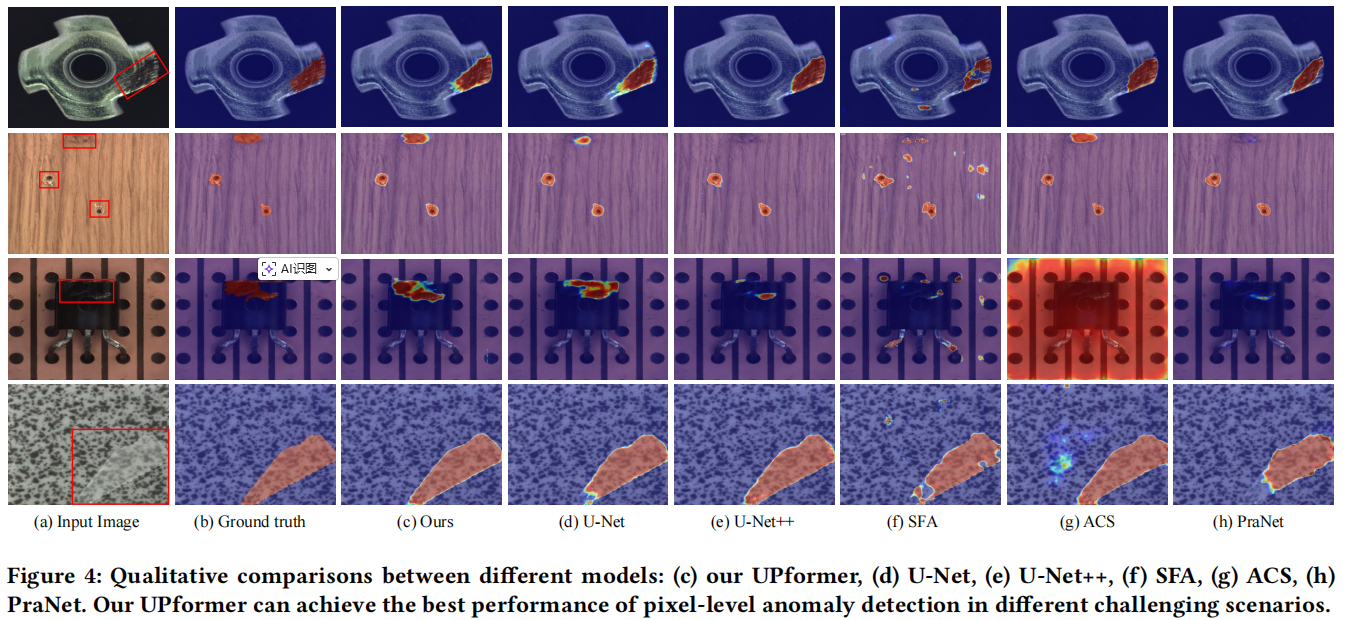
图4展示了我们提出的UPformer与其他对比方法的可视化结果。可以明显看出,我们的模型在不同场景中均能实现最佳的异常检测性能。与其他SOTA相比,我们可观察到UPformer具有两大优势。一方面,UPformer的结果具有内部一致性,其生成的异常图边缘与真实异常图更为相似。这得益于我们模型强大的异常多样性捕捉能力。具体而言,记忆引导原型编码器(MPE)对不同异常进行聚类,随后将学习到的聚类中心存储至记忆库,从而帮助模型识别各类异常。综上所述,图4的可视化结果进一步证实了我们UPformer的有效性和优越性。
4.4 消融研究
我们通过实验验证了UPformer中各模块的设计贡献,具体结果详见表3。
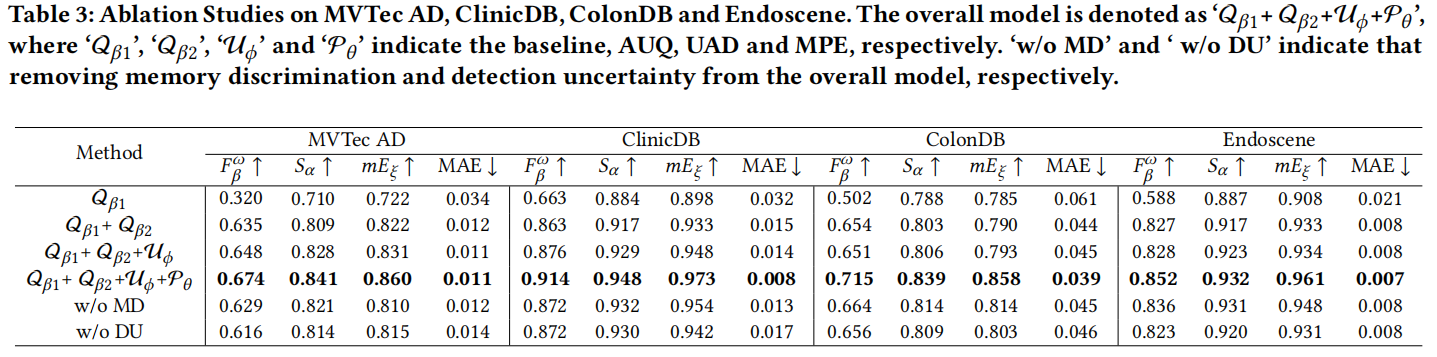
整体模型结构为‘ Q𝛽1 + Q𝛽2 + U𝜙 + P𝜃 ’,其中‘ Q𝛽1 ’、‘ Q𝛽2 ’、‘ U𝜙 ’和‘ P𝜃 ’分别对应基线模型、 AUQ 、 UAD 和MPE的使用。首先采用基线 Q𝛽1 进行异常检测,如表3首行所示,其性能表现未达预期。
AUQ 的影响
作为概率模型, AUQ(Q𝛽1 +
Q𝛽2)通过从概率分布中抽取40个样本计算均值,生成异常检测图。显然,借助
AUQ 模块,我们的模型性能显著提升。此外, AUQ 还提供量化器 Q𝛽2
,用于计算异常检测的不确定性,该工具可应用于后续模块。
UAD 的影响
随后,我们为 AUQ 配备了 UAD \(\mathcal U_{\phi}\)
。值得注意的是,此处使用的 UAD
并未从MPE获取学习到的异常原型表示。通过对比表3的第二行和第三行数据,我们可以发现
UAD 在所有数据集上均在四项评估指标上获得性能提升,这证明了 UAD
的有效性。这归因于 UAD
使我们的模型能够利用多重检测的额外统计信息,在不确定区域准确识别异常,从而提升模型的异常检测性能。
MPE的影响
此外,MPE被整合到整体模型中,表示为‘
Q𝛽1 + Q𝛽2 + U𝜙 + P𝜃
’。通过对比表3第三行和第四行的结果,借助MPE,模型性能显著提升。这是因为MPE能够捕捉异常的高层次语义信息,使模型能确保同类异常的表征一致性。
记忆判别机制的影响
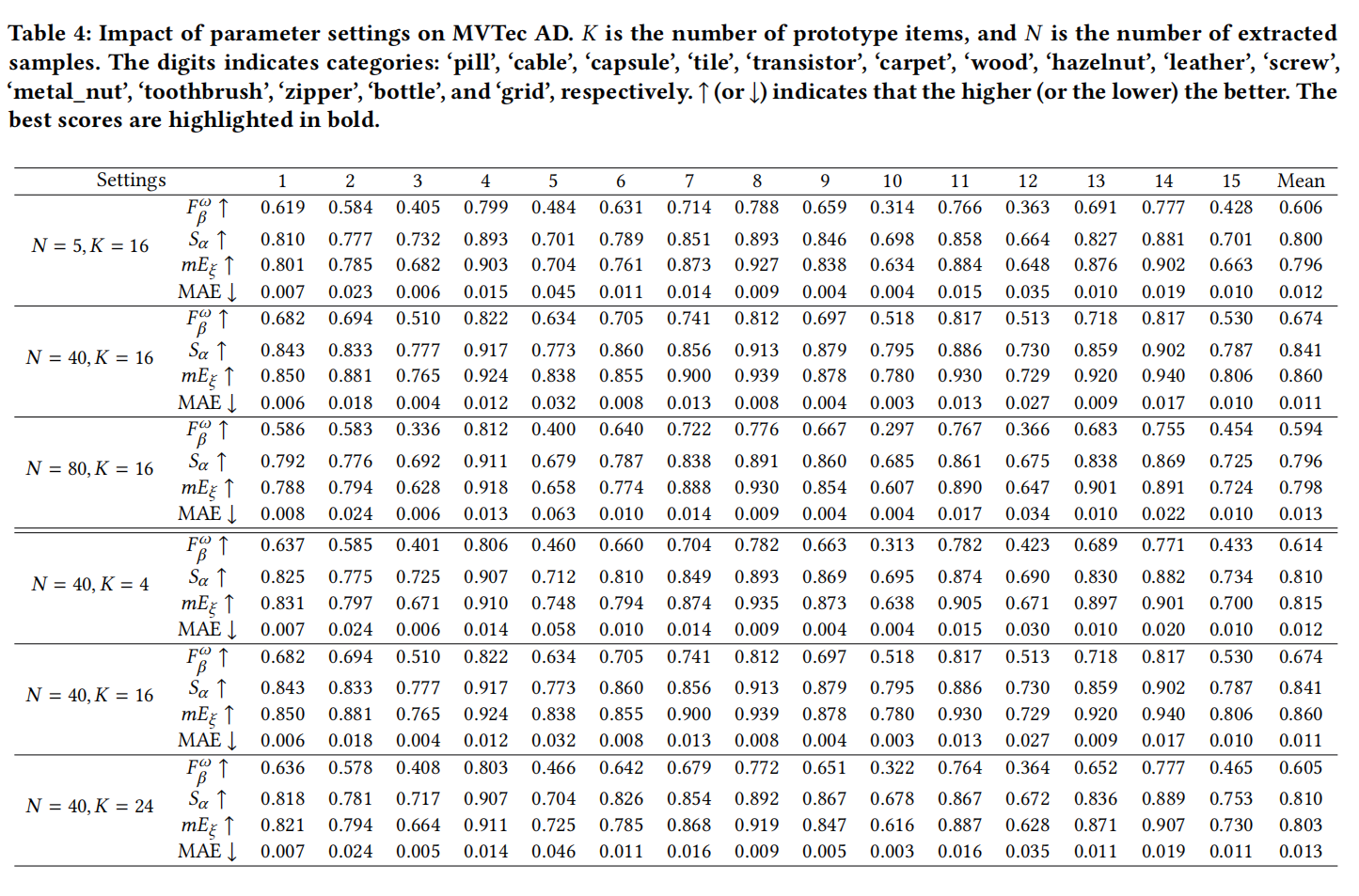
该机制通过使原型表征彼此保持较大距离,旨在增强记忆模块所学原型表征的判别能力。为验证其有效性,我们在表3第五行移除了记忆判别机制并展示性能。可见,未使用记忆判别损失函数训练的模型性能较整体模型急剧下降,这表明记忆判别损失的有效性。此外,表4显示
𝐾 =16的原型配置能使模型取得显著性能提升。
检测不确定性的影响
异常检测不确定性估计用于引导模型在训练阶段更加关注不确定区域。为验证其影响,我们将其从整体模型中移除,并在表3第六行展示结果。显然,与完整配置模型相比,未包含检测不确定性的模型在所有数据集上的表现均显著下降,这表明不确定性估计能使模型获得更优的视觉异常检测性能。如表4所示,当提取
𝑁 =40个样本进行不确定性估计时,模型可获得最优性能。

图5:不确定性图可视化。(a) 输入图像;(b) 异常检测不确定性;(c) 真实值;(d) 无不确定性结果;(e) 带有不确定性的结果。
异常检测不确定性的可视化呈现
图5展示了异常检测不确定性的多种可视化结果。可以看出,检测不确定性突出了正常区域与异常区域之间的边界,这表明这些区域会干扰深度异常检测模型的判断。我们的观察结果与实际情况一致:异常区域与其正常环境之间的模糊边界,正是视觉异常检测面临的核心挑战。与未使用不确定性辅助的检测结果相比,最终检测结果在不确定性辅助下能更准确地识别边界。
5 结论
本文提出了一种结合不确定性与原型感知的异常检测Transformer(UPformer)。该模型将记忆增强模块与贝叶斯神经网络嵌入Transformer架构,通过融合原型学习与不确定性估计的优势,有效捕捉异常的多样性特征与不确定性特征。具体而言,采用记忆引导的原型编码器学习并存储各类异常的典型特征表示;通过异常检测不确定性量化器学习异常检测结果的分布规律,从而评估检测的不确定性;同时引入不确定性感知的异常解码器,利用学习到的异常典型特征与检测不确定性进行识别。这种不确定性机制促使模型聚焦于不确定区域。实验结果表明,UPformer的性能优于当前主流方法。未来我们将引入时间信息,拓展UPformer在视频异常检测中的应用。