Pre-training-free Image Manipulation Localization through Non-Mutually Exclusive Contrastive Learning

$\text{Jizhe Zhou}^{1,4},\text{Xiaochen Ma}^{1,4},\text{Xia Du}^{2,4},\text{Ahmed Y}.\text{Alhammadi}^{3,4},\text{Wentao Feng}^{1,4*}$ 1四川大学计算机科学学院 2厦门理工大学计算机与信息工程学院 3 Mohamed Bin Zayed大学战略事务办公室 4中国教育部机器学习与产业智能工程研究中心

摘要

深度图像操作定位（IML）模型存在训练数据不足，严重依赖于预训练。我们认为对比学习更适合于解决IML的数据不足问题。形成相互排斥的正性与负性是对比学习的先决条件。然而，当在IML中采用对比学习时，我们遇到了三类图像补丁：篡改、真实和轮廓补丁。篡改和真实的补丁自然是相互排斥的，但是包含篡改和真实像素的轮廓补丁对它们不是相互排斥的。
简单地取消这些轮廓补丁会导致巨大的性能损失，因为轮廓补丁对学习结果是决定性的。因此，我们提出了非互斥对比学习（NCL， Nonmutually exclusive Contrastive Learning）框架来从上述困境中拯救传统的对比学习。在NCL中，为了应对非互斥性，我们首先建立一个具有双分支的枢轴结构，在训练时不断地在正和负之间切换轮廓补丁的作用。然后，我们设计了一个枢轴一致的损失，以避免由角色转换过程造成的空间损坏。
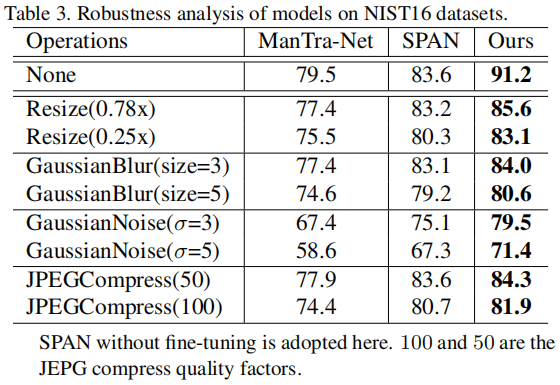
通过这种方式，NCL既继承了自监督的优点来解决数据不足，又保留了较高的操作定位精度。大量的实验证明，我们的NCL在没有任何预训练的情况下，在所有五个基准测试上都达到了最先进的性能，并且在看不见的真实样本上更鲁棒。

1. 引言

媒体技术的惊人进步使我们更容易地获得操作图像。图像处理定位（IML）是防御性信息取证中必不可少的一部分，并得到了信息安全行业的大量投资。今天，数据不足是构建深度IML模型中最突出的问题。由于用于篡改识别的密集注释和专业知识过高，IML的公共数据集都很小（有几百到几千张图像），严重不足以训练深度cnn。因此，主要的深度IML方法在额外的大规模数据集上进行预训练。
一般来说，IML模型的预训练依赖于综合数据集。一方面，合成数据集消除了较高的标记成本，对合成数据集的预训练避免了过拟合。另一方面，使用综合数据集进行预训练会阻碍模型之间的公平比较，甚至危及模型的通用性。预训练对模型的性能至关重要，为了公平比较，同一任务的模型通常在同一数据集上进行预训练。然而，IML模型的合成预训练数据集在注释数量和质量上存在显著差异。例如，ManTra-Net [34]基于一个自收集的、像素标记的数据集102,028张图像和385种操作类型进行预训练；RGBN [38]采用了超过42000张图像的随机合成数据集；星网[33]包含100,000张复制移动图像的合成数据集用于预训练；MVSS [9]采用84000张图像的合成数据集。对在不同的合成数据集上预先训练的模型进行忠实的评估变得不可能了。此外，与真实的篡改图像不同，这些天真合成的图像严重缺乏复杂的后处理来覆盖它们的操作痕迹或伪影[5,29,9]。换句话说，合成数据集的采样过程偏向于人工构建数据集[36,37]的采样过程。在这样一个具有抽样偏差的数据集上学习的模型在通用性上很短，并且在很小的、非同源的基准上测量这种模式不能完全揭示其在真实情况下的糟糕性能。

总之，我们的主要贡献是四重的：

没有额外的数据。据我们所知，我们是第一个在IML中引入对比学习来解决训练数据的不足和训练前造成的缺陷的工作。
非相互排斥的对比。据我们所知，我们也是第一个通过对比学习处理非互排他的三边关系。我们的非互斥对比学习（NCL，Non-mutually exclusive Contrastive Learning）框架可以服务于其他任务，如语义分割或目标细粒度检测。
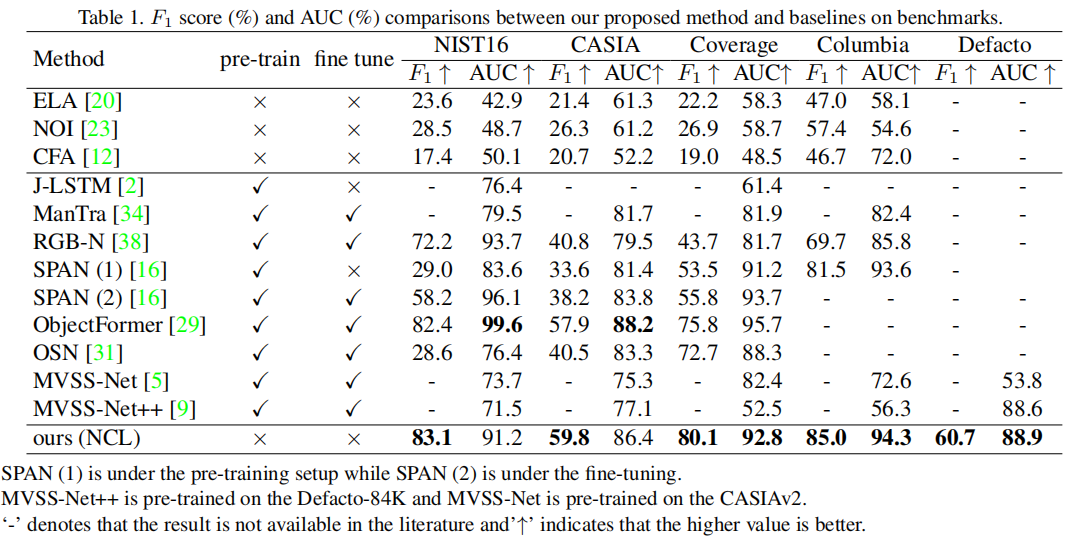
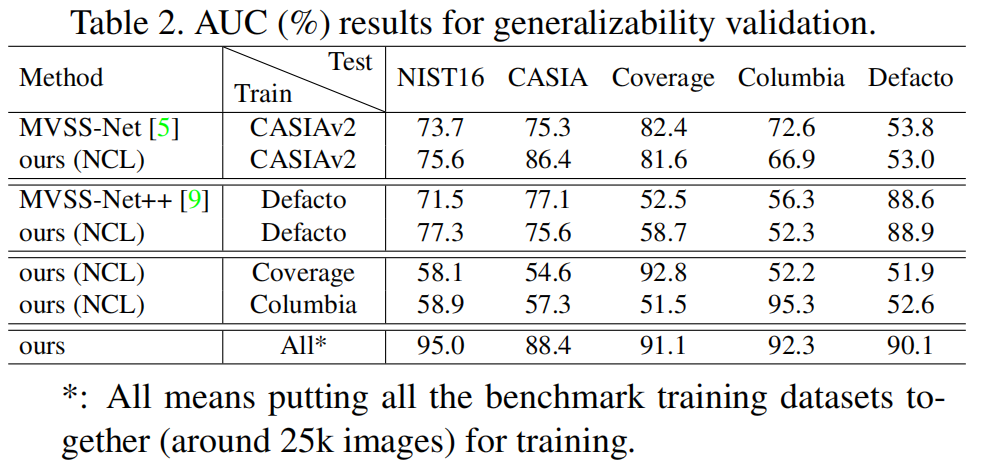
最高的基准性能。我们的方法使用较少和较差的训练数据，但在所有五个公共基准上取得了最先进的性能以及最高的模型泛化能力。
插件价值。我们的方法功能可以基于CNN风格和Transformer风格的骨干网络。主干选择不会破坏NCL的完整性。

3. 方法

3.1 基本的编码器-解码器结构

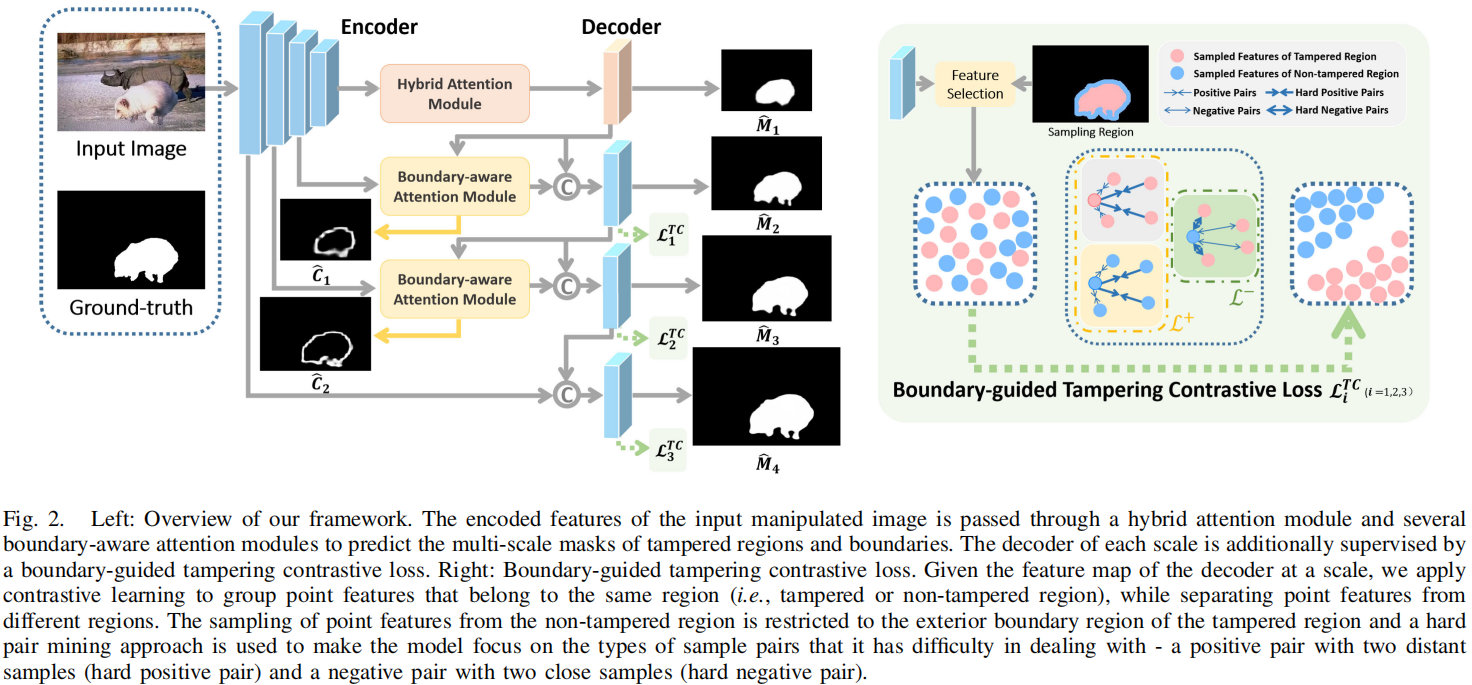
我们采用DeepLabV3+ [4]作为我们的IML模型的基本编码-解码器结构，因为它已经被许多其他IML模型作为基线[13,9]。请注意，基本模式选择或主干模式选择会影响我们的NCL的有效性。因此，图2中的编码器主干是ResNet101 [15]块，在最后几个块中存在空洞卷积。同样应用了空间空间金字塔池（ASPP）块。然后，所编码的大小特征（64×64）被传递给解码器。该解码器采用了两个上采样模块。编码器的输出被两次上采样到4倍。简而言之，我们的基本编码器-解码器应用了与DeepLabV3+模型相同的网络结构和训练设置。

3.2 非互斥对比学习

3.2.1 问题公式

对于传统的对比学习，将问题域定义为通用集$\mathbb{U}$。如图1中传统的对比学习部分所示，我们有集合的正类$\mathbb{P}$，集合的负类$\mathbb{N}$，其中： \[\begin{aligned}\mathbb{P}\cup\mathbb{N}&=\mathbb{U}\\\mathbb{P}\cap\mathbb{N}&=\emptyset\end{aligned}\] $\emptyset$表示正类与负类的互斥性。将$p$标记为一个被篡改的图像补丁，是$\mathbb{P}$的一个元素。对于$\forall p\in\mathbb{P}$，我们进一步表示$p_{j}\in\mathbb{P},p_{j}\neq p$；和$n_i\in\mathbb{N}$。那么，传统的对比学习目标是： \[\arg\max_{f}\{\sum_{i i}\phi(f(p),f(n_{i}))-\phi(f(p),f(p_{j}))\}\] $f(\cdot)$是一个图像patch的学习特征表示。$f(p_{j})$和$f(n_{j})$为图2中IML特征图中的红色和蓝色立方体，$\phi(\cdot,\cdot)$表示两个特征向量之间的测量距离，即相似度。本文的符号是统一的，其中图像块集用大写字母表示，图像块用小写字母表示，$f(\cdot)$函数是图像块的学习特征表示。

然而，对于图1所示的NCL，我们有： \[\begin{aligned}&\mathbb{N}\cup\mathbb{P}\cup\mathbb{C}=\mathbb{U}\\&\mathbb{P}\cap\mathbb{N}=\emptyset;\mathbb{C}\cap\mathbb{N}=\mathbb{C}^-;\mathbb{C}\cap\mathbb{P}=\mathbb{C}^+\end{aligned}\] $\mathbb{C}$是所有轮廓补丁的集合。$\mathbb{C}^+$和$\mathbb{C}^-$表示为$\mathbb{C}$与正集和负集的交点。这意味着正像素和负像素混合在轮廓补丁中。对于对比学习，通过在同一集合中找到另一个元素，可以很容易地形成正对。根据(1)和(2)，空的交点意味着如何形成重要的负对。因此，我们首先将(3)与(1)修改为完全相同的格式。用一些小技巧，我们就可以有： \[\begin{aligned}&\mathbb{N}\cup\mathbb{P}\cup\mathbb{C}=\mathbb{U}\\&\mathbb{P}\cap\mathbb{N}=\mathbb{C}^+\cap\mathbb{N}=\mathbb{C}^-\cap\mathbb{P}=\emptyset\end{aligned}\] 然后，根据(1)，我们现在可以将(3)中所写的非互斥对比转换为（$\mathbb{P}\cap\mathbb{N}$）、（$\mathbb{C}^+\cap\mathbb{N}$）和（$\mathbb{C}^-\cap\mathbb{P}$）之间的三个二进制对比。为了进行三对比较，我们首先需要找出(3)中定义的$\mathbb{C}^+$和$\mathbb{C}^-$。$\mathbb{C}^+$和$\mathbb{C}^-$也是补丁片段或像素。基本的编码器网络不能产生补丁片段的特征。因此，我们设计了枢轴网络，直接使用轮廓块作为输入，并生成C+和C−的特征表示。也就是说，枢轴网络通过学习（$\mathbb{C}\cap\mathbb{C}^+$）和（$\mathbb{C}\cap\mathbb{C}^-$）之间的两个映射函数来切换轮廓斑块的作用。自然地，枢轴网络应该拥有两个具有相同输入的相似分支。

3.2.2 枢轴网络

在构建支点网络的详细布局之前，我们需要进一步考虑支点网络的输入。训练枢轴网络也需要足够的轮廓补丁。但是，如果我们选择一个较小的斑块大小来生成更多的轮廓斑块。小的补丁大小导致一个图像补丁中的少量像素。那么，$\mathbb{C}^+$和$\mathbb{C}^-$中的一些元素可能包含少量的像素，不适合训练枢轴网络。因此，在单个图像中，我们将所有的轮廓块特征连接到一个完整的嵌入$\mathfrak{p}$中，并发送$\mathfrak{p}$作为枢轴网络的输入，以确保学习结果足够显著地进行比较。

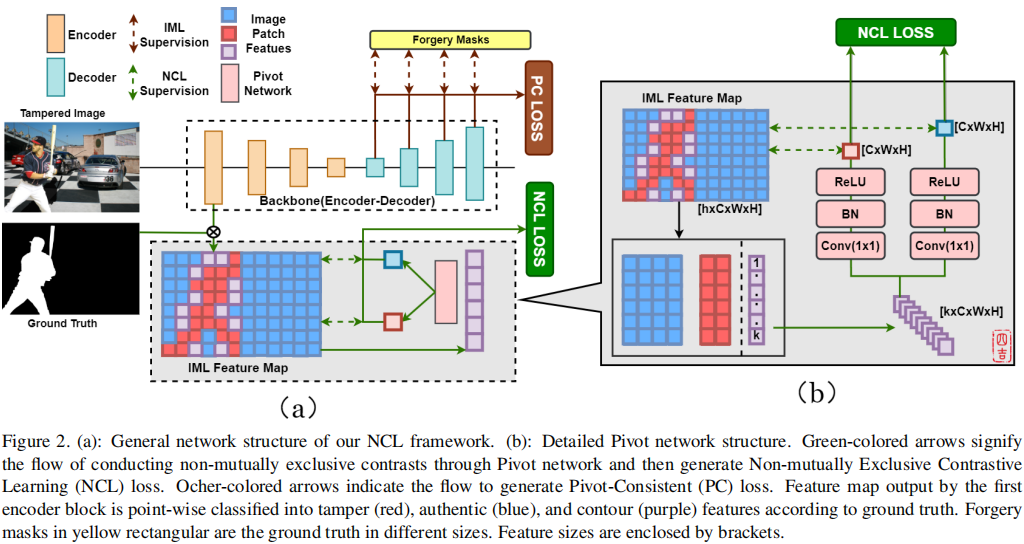
图2。 (a): 我们的NCL框架的一般网络结构。 (b): 详细的透视图网络结构。绿色箭头表示通过枢轴网络进行非互斥对比，然后产生非互斥对比学习（NCL）损失。赭色的箭头表示产生枢轴一致（PC）损失的流量。第一个编码器块输出的特征图根据地面真相，按点方向分为篡改（红色）、真实（蓝色）和等高线（紫色）特征。黄色矩形的伪造面具是不同大小的地面真相。功能尺寸用方括号表示。

在图2中，这个连接将紫色的立方体组装成一条大小的条带（$k\times C\times W\times H$）。$k=card(\mathbb{C})$。C、W、H是一个轮廓特征的通道、高度和宽度。$card()$表示基数或集$\mathbb{C}$中的元素数。一方面，利用$k=card(\mathbb{C})$，我们将轮廓块特征连接成一个向量（$k\times C\times W\times H$）。该向量将整个图像中的轮廓块特征聚集在整个图像中，以解决当存在少数轮廓块时的模型效率低下的问题。另一方面，枢轴网络将这个（$k\times C\times W\times H$）向量平化为一个固定大小的（$1\times C\times W\times H$）向量。这进一步有助于处理特征处理中k的不同大小。
枢轴网络的详细结构如图2 (b)所示，通过粉红色的矩形和绿色的箭头表示。
然后，我们为我们的枢轴网络设计了两个对称的分支。这些分支共享相同的输入和具有相同的结构。$\mathfrak{p}$是由（1×1）卷积产生的第一个过程。这个（1×1）卷积核使$\mathfrak{p}$扁平化为（$1\times C\times W\times H$）的形状。此外，这个（1×1）核将p投射到一个潜在的Hilbert空间$\mathcal{H}:\mathbb{R}^{C\times W\times H}$，其中$f(p_{j})$和$f(n_{j})$确定，特征之间的相似性可以用$\phi(\cdot,\cdot)$均匀地度量。BN和ReLU是批处理规范化层和ReLU激活层。
枢轴网络在输入集$\mathbb{C}$（$c\in\mathbb{C}$）和输出集$\mathbb{C}^+$（$c\in\mathbb{C}^+$）和$\mathbb{C}^-$（$c\in\mathbb{C}^-$）之间构造反射f（·）。因此，$f(\cdot)$应满足：
(1). $\mathbb{C}^+$和$\mathbb{C}^-$有利于IML的精度；
(2). $\mathbb{C}^+$和$\mathbb{C}^-$是平滑的流形，以保证NCL损失的反向传播。由于$\mathbb{C}$是一个光滑的流形（受限于Euclidean空间)，所以$f(\cdot)$应该是一个双射体；
(3). 反射后无信息丢失。这意味着我们可以通过一些二进制操作$(\cdot)$将${c}^+$和${c}^-$组合回${c}$；$c^+\cdot c^-=c,c^+\cdot c=c,c^-\cdot c=c.$。
因此，我们可以有一个组$(G,\cdot)$，其中$G=\mathbb{C}^+\cup\mathbb{C}^-$。G是一个李群，因为：
根据(2)，组逆$G\to G$是平滑的。
根据(3)，组乘$G\times G\to G$是平滑的。
因此，枢轴网络（${c}^+$和${c}^-$）的输出是李群元素。然后，我们将枢轴网络作为一个光滑的映射函数，并从李群中借用$\mathfrak{se}$符号。我们将这两个分支的输出写成$\mathfrak{se}^+(\mathfrak{p})$和$\mathfrak{se}^-(\mathfrak{p})$。$\mathfrak{se}^+(\cdot)$和$\mathfrak{se}^-(\cdot)$只是表示由枢轴网络学习到的特征变换函数；我们不能保证它们是微分流形。$\mathfrak{se}^+(\mathfrak{p})$和$\mathfrak{se}^-(\mathfrak{p})$是在图2 (b)中得到的浅红色和浅蓝色的立方体。$\mathfrak{se}^+(\cdot)$和$\mathfrak{se}^-(\cdot)$的集合是所期望的$\mathbb{PI}^{+}$和$\mathbb{PI}^{-}$。对$\mathfrak{se}^+(\cdot)$和$\mathfrak{se}^-(\cdot)$的直观解释是，它们是由枢轴网络生成的特征$\mathfrak{p}$压缩出来的特殊的正负特征；而常见的正负特征是由主干网络根据物理上存在的图像补丁产生的。从这个角度来看，枢轴网络就像钟摆一样在正与负之间摆动枢轴的作用。
基于H中的$f(\cdot)$和$\phi(\cdot,\cdot)$、$\mathfrak{se}^+(\cdot)$和$\mathfrak{se}^-(\cdot)$，我们将NCL的学习目标表述为： \[&\arg\max_{f,s \mathbf{c}^{+},\mathbf{s}^{-}}\{\sum_{i,j}\phi(f(p),f(n_{i}))-\phi(f(p),f(p_{j}))\}+\\&\{\sum_{i,j}\phi(\mathfrak{s}\mathfrak{c}^{+}(\mathfrak{p}),\mathfrak{s}\mathfrak{c}^{-}(\mathfrak{p}))-\phi(\mathfrak{s}\mathfrak{c}^{+}(\mathfrak{p}),f(p_{j}))\}+\\&\{\sum_{i,j}\phi(\mathfrak{s}\mathfrak{c}^{+}(\mathfrak{p}),\mathfrak{s}\mathfrak{c}^{-}(\mathfrak{p}))-\phi(\mathfrak{s}\mathfrak{c}^{-}(\mathfrak{p}),f(n_{i}))\}\]

3.2.3 非互斥的对比度损失

我们确实可以根据(5)构造NCL损失函数。但是，由于轴网络为每个被操纵的图像产生一个$\mathfrak{se}^+(\mathfrak{p})$和$\mathfrak{se}^-(\mathfrak{p})$，$\phi(\mathfrak{se}^+(\mathfrak{p}),\mathfrak{se}^-(\mathfrak{p}))$独立于和参数$i,j$，并在损失积累过程中成为一个常数。这样的常数破坏了对比对的多样性。因此，我们在正对的构建中做了一些小的替换，并进一步细化(5)为： \[&\arg\max_{f,\mathfrak{sc}^+,\mathfrak{sc}^-}\{\sum_{i,j}\phi(f(p),f(n_i))-\phi(f(p),f(p_j))\}+\\&\{\sum_{i,j}\phi(\mathfrak{sc}^+(\mathfrak{p}),f(n_i))-\phi(\mathfrak{sc}^+(\mathfrak{p}),f(p_j))\}+\\&\{\sum_{i,j}\phi(\mathfrak{sc}^-(\mathfrak{p}),f(p_j))-\phi(\mathfrak{sc}^-(\mathfrak{p}),f(n_i))\}\] 通过我们的枢轴网络，在(6)中，NCL将三边图像补丁之间的非互斥关系改革为三个由“+”连接的互斥、成对的二值比较。这是由图2中的NCL监督绘制的。为了简化，我们让$p = p_m$分配一个下标；标记$e_{x}^{y} = (f(x),f(y))/$，$e_{x}^{-} = (^{{-}(),f(x))/$和$e_{x}}{+} = (^{+}(),f(x))/$，其中$$是温度参数。参考(6)，NCL损失函数为：$$L_{NCL}=\frac1{m\times j}\sum_m\sum_j\log\frac{e_{p_m}^{p_j}}{e_{p_m}^{p_j}+\sum_ie_{p_m}^{n_i}}+\frac1j\sum_j\log\frac{e_{p_j}^+}{e_{p_j}^++\sum_ie_{n_i}^+}+\frac1i\sum_i\log\frac{e_{n_i}^-}{e_{n_i}^-+\sum_je_{p_j}^-}$$ 最后但并非最不重要的是，我们探索了实施支点网络的确切位置。之前的一些工作[3]截断了不同层的深度cnn，揭示了早期截断的网络为伪造检测提供了更好的特征。此外，早期截断的网络布局浅，接收场小，大特征图，理想地满足NCL小块尺寸的要求。然后，我们将ResNet101划分为卷积块，如在他们的论文[15]中所述，并探索由每个ResNet101块产生的特征图。如预期的那样，实验结果验证了第一个块后的特征图是最合适的。在实验部分，我们提供了更多关于NCL图像补丁大小选择的详细信息。

3.3 枢轴一致性损失

枢轴网络对连接的轮廓块进行卷积，破坏了轮廓块内部和之间的空间相关性。[16]已经表明，空间信息在IML中是至关重要的。因此，我们在解码器侧开发了一个枢轴一致性（PC，Pivot Consistent）损失，以确保轮廓斑块的空间相关性在枢轴网络后仍然存在。PC损失在基本的像素级BCE损失中为轮廓像素分配额外的权重$\mu$，以加强轮廓像素之间的空间连接。然而，轮廓像素的数量远远少于操纵或真实的像素。为了避免过拟合，如图2 (a)中解码器侧的赭色箭头所示，我们使用辅助分类器[7]，在每个上采样过程中逐步累积PC损失。每次上采样后，我们将ground truth缩小到与特征图相同的大小；然后，可以通过缩小的伪造掩模进行像素级的IML监督。我们在这里略滥用小写字母的符号。$t$表示图像中的像素，$\hat t$表示轮廓像素，$\mu$表示额外的权重。$\gamma(\cdot)$是一个像素的地面真实标签，$\theta(\cdot)$是我们的网络对一个像素的预测标签。$\gamma(\cdot)$和$\theta(\cdot)$提供二进制值作为输出。那么，我们的PC损失是： \[L_{PC}=\frac{\mu}{\hat{t}}\sum_{\hat{t}}(\gamma(\hat{t})\log(\theta(\hat{t}))+(1-\gamma(\hat{t}))\log(1-\theta(\hat{t})))+\frac{(1-\mu)}t\sum_t(\gamma(t)\log(\theta(t))+(1-\gamma(t))\log(1-\theta(t)))\] 我们发现较大的$\mu$有利于最终的IML精度。对$\mu$的评估详见实验部分。