Robust deep fuzzy K-means clustering for image data
Robust deep fuzzy K-means clustering for image data
Xiaoling Wu , Yu-Feng Yu\(^{a,∗}\) ,
Long Chen\(^ b\) , Weiping Ding\(^ c\) , Yingxu Wang\(^ d\)
a 广州大学统计系, 中国广州
b 澳门大学计算机与信息科学系, 中国澳门
c
南通大学信息科学与技术学院, 中国南通
d
济南大学网络智能计算山东省重点实验室, 中国济南
摘要
图像聚类是计算机视觉中的一项艰巨任务,具有重要的应用价值。这项任务的关键是图像特征的质量。目前,大多数的聚类方法都面临着这一挑战。也就是说,特征学习和聚类的过程是独立运行的。为了解决这个问题,一些研究人员已经致力于一起进行特征学习和深度聚类。然而,所获得的特征缺乏成功处理高维数据的可鉴别性。为了解决这一问题,我们提出了一种新的鲁棒深度模糊𝐾-means聚类(RD-FKC,robust deep fuzzy 𝐾-means clustering)模型,该模型有效地将图像样本投影到一个具有代表性的嵌入空间中,并将隶属度精确地学习到一个组合框架中。具体来说,RD-FKC引入了拉普拉斯正则化技术来保持数据的局域性。此外,通过使用自适应损失函数,该模型对不同类型的异常值具有更强的鲁棒性。此外,为了避免潜在空间的扭曲,使提取的特征尽可能地保留原始信息,该模型引入了重构误差,并对网络参数进行了正则化处理。最后,给出了一种求解优化模型的有效算法。我们已经进行了大量的实验,说明了RD-FKC相对于现有的聚类方法的优势和优越性。
1.介绍
本文提出了一种新的深度聚类模型,即鲁棒深度模糊𝐾-均值聚类(RD-FKC),该模型将模糊聚类和深度卷积自动编码器(DCAE)集成到一个统一的框架中。图1显示了RD-FKC的框架。
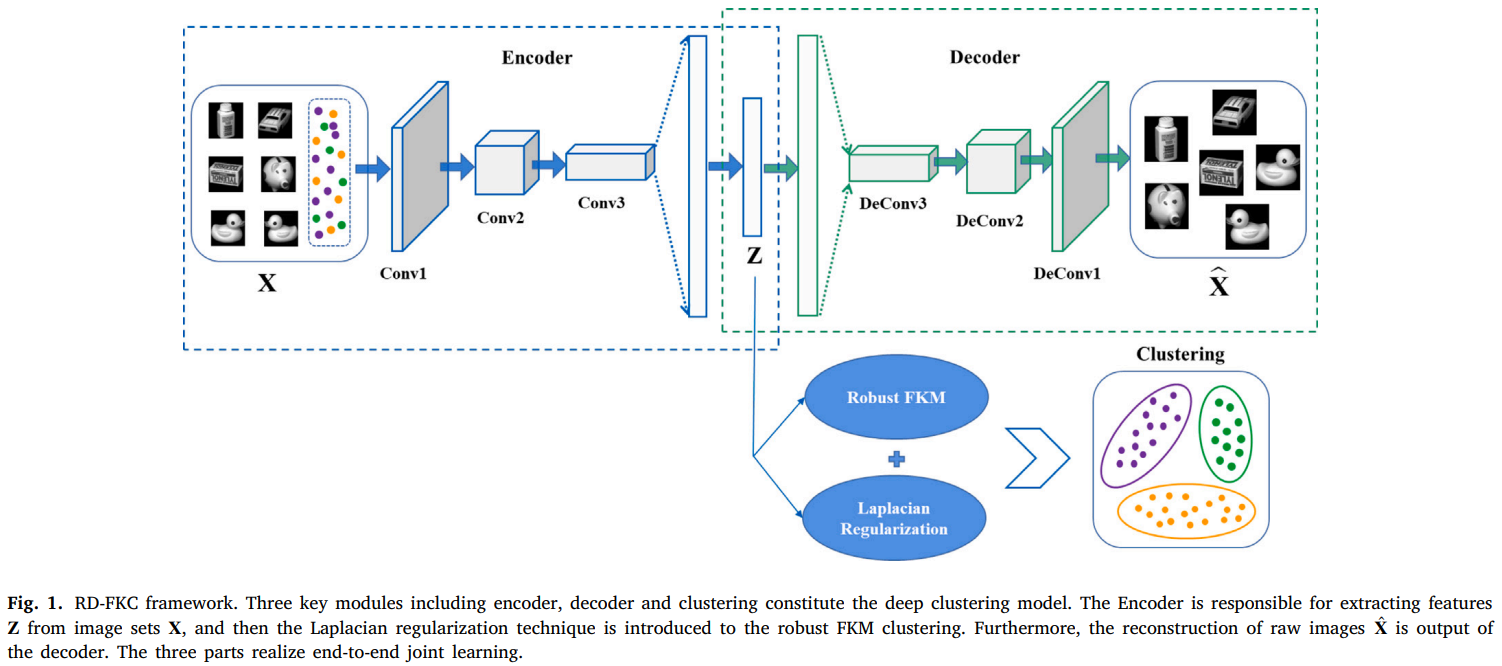
具体来说,我们使用拉普拉斯正则化来约束隶属度矩阵,并在嵌入特征空间中执行FKM,这不仅可以保证使用DCAE提取高维图像数据中包含的复杂和抽象信息,还可以获得局部信息,提高聚类性能。受[29]的启发,我们的模型引入了自适应损失函数,使聚类过程更加鲁棒。本文的主要贡献包括:
- 将聚类嵌入到深度卷积自动编码器中,使DCAE能够学习有区别的和有代表性的特征进行聚类,然后聚类结果进而促进特征学习。也就是说,RD-FKC的目标是同时进行特征学习和聚类。
- 利用拉普拉斯正则化方法对隶属度矩阵进行约束,使从相似样本中学习到的隶属度也相互关联。也就是说,隶属度之间的联系与约束下的样本一致,可以进一步保存图像的局部信息。
- RD-FKC将自适应损失函数引入到统一的框架中,可以减少各种异常值的影响,有助于增强聚类的鲁棒性。
- 提出了一种有效的算法来优化该框架。同时,该框架是直接端到端训练的,而不需要任何繁琐的预训练过程。一系列的比较实验证实了该模型的有效性和优越性。
本文后续部分的组织结构如下。第2节给出了关于模糊𝐾-均值聚类和深度卷积自动编码器的一些相关工作。第3节阐述了所提出的RDFKC模型和有效算法。比较实验和结果分析详见第4节。最后,我们将在第5节中结束该工作。
2.相关工作
2.1.符号
在本文中,我们定义一个向量与一个粗体小写字母,例如𝐱,矩阵和一个粗体大写字母,例如𝐗,\(𝐱_𝑖\)表示矩阵𝐗的第\(i\)列,\(𝐱^𝑖\)表示它的第\(i\)行,\(𝑥_{𝑖𝑗}\)是矩阵𝐗的第\(i\)行和第\(j\)列元素。将\(\{ \bf X_{n}\}_{n=1}^{N}\)作为具有𝑁张图像的图像集,提取的相关特征为\(\mathbf{Z}=\left[\mathbf{z}_{1},\mathbf{z}_{2},\ldots,\mathbf{z}_{N}\right]\in\mathbb{R}^{d\times N}\)。这里,𝑑是嵌入式空间的维数。RD-FKC的目的是获得区别表示𝐙,并将其聚类为𝐶组。将\(\mathbf{U}=[\mathbf{u}_{1}^{T},\mathbf{u}_{2}^{T},\ldots,\mathbf{u}_{N}^{T}]^{T}\in\mathbb{R}^{N\times C}\)和\({\bf V}=[{\bf v}_{1},{\bf v}_{2},\dots,{\bf v}_{C}]\,\in\,\mathbb{R}^{d\times C}\)分别定义为隶属度矩阵和簇中心矩阵。表1列出了更多的字符,并解释了它们在首次被介绍时的含义。

2.2.模糊𝐾-means聚类
模糊𝐾-means聚类[4]是𝐾-means的一个模糊版本,其目的是构造隶属度矩阵,然后温和地将样本划分为相应的类别。FKM的目标函数定义为:
\[\begin{array}{l}{\operatorname*{min}\mathcal{L}(\mathbf{U},\mathbf{V})=\sum_{n=1}^{N}\sum_{c=1}^{C}u_{n
c}^{m}||\mathbf{x}_{n}-\mathbf{v}_{c}||_{2}^{2}}\\{\mathrm{s.t.}\quad\sum_{c=1}^{C}u_{n
c}=1,0\leq u_{n c}\leq1}\end{array}\] 其中,\(m(m>1)\)是一个模糊化参数。\(𝐱_𝑛\)表示第n个样本点。\({\textbf{U}}={\lbrack{u_{n c}\rbrack}_{N\times
C}}\)为隶属度矩阵,\(𝑢_{𝑛𝑐}\)表示分配给第n个样本点的第𝑐类的隶属度。\(\mathbf{V}=\left[\mathbf{v}_{1},\mathbf{v}_{2},\ldots,\mathbf{v}_{C}\right]\)是集群中心矩阵,\(\mathbf{v}_{c}\,\in\,\mathbb{R}^{d}\)是第𝑐个集群。
然后,利用拉格朗日乘子,根据以下公式交替更新\(𝑢_{𝑛𝑐}\)和\(\mathbf{v}_{c}\): \[u_{n c}=\frac{1}{\sum_{l=1}^{C}(\frac{||{\bf
k}_{n}-{\bf v}_{c}\,||_{2}^{2}}{||{\bf k}_{n}-{\bf
v}_{l}||_{2}^{2})})^\frac{2}{m-1}}\]
\[\mathbf{v}_{c}={\frac{\sum_{n=1}^{N}u_{n c}^{m}\mathbf{x}_{n}}{\sum_{n=1}^{N}u_{n c}^{m}}}\]
2.3.深度卷积自动编码器(DCAE)
一个经典的自动编码器通常是由全连接的层组成的,它忽略了图像的结构,并进一步引入了大量的参数。与之相比,DCAE [30]具有本地连接和权重共享的特点,更适合用于图像处理任务。为了利用图像中包含的空间信息,给定一个单通道图像𝐗,将DCAE的编码器和解码器定义为: \[{\bf G}^{p}={\cal F}_{e}({\bf X}*{\bf W}^{p}+a^{p})\]
\[\hat{\bf X}={\cal F}_{d}(\sum_{p}{\bf G}^{p}*\tilde{\bf W}^{p}+b)\]
其中,𝐆𝑝为𝑝th特征映射,∗为卷积运算。\({\cal F_e}\)和\({\cal
F_d}\)是非线性激活函数(我们在实验中使用ReLU)。下标𝑒和𝑑分别表示编码器和解码器。\({\bf W}^{p}\)是过滤器,\(\tilde{\bf
W}^{p}\)是翻转操作,可以将嵌入表示恢复到原始大小的位置。\(𝑎^𝑝\)和𝑏是相应的偏差。
DCAE通过最小化重构误差来更新编码器和解码器的参数:
\[\mathcal{L(\Delta)}=\frac{1}{N}\sum_{n=1}^{N}\|F_{d}(F_{e}(\mathbf{X}_{n}))-\mathbf{X}_{n}\|_{F}^{2}\]
其中𝑁为图像数量,\(\Delta\)包含所有网络参数。‖⋅‖𝐹表示一个矩阵的Frobenius范数。
3.鲁棒的深度模糊𝑲-means聚类
3.1.自适应损耗函数
假设𝐇是一个任意矩阵,\(l_{2,1}\)规范表示为\(\|\mathbf{H}\|_{2,1}=\sum_{i}||\mathbf{h}^{i}||_{2}\)对大损失很鲁棒,但对小损失很脆弱,而平方Frobenius规范表示为\(\|\mathbf{H}\|_{F}^{2}\ =\
\sum_{i}\|\mathbf{h}^{i}\|_{2}^{2}\)很容易解决,对小损失稳健,但对大损失敏感。因此,一个结合了这两种优点的自适应损失函数被定义为:
\[||\mathbf{H}||_{\tau}=\sum_{i}{\frac{(1+\tau)||\mathbf{h}^{i}||_{2}^{2}}{\|\mathbf{h}^{i}\|_{2}+\tau}}\]
这里的𝜏>0是一个自适应参数。如果𝜏→0,‖𝐇‖𝜏→‖𝐇‖2,1。如果𝜏→∞,‖𝐇‖𝜏→‖𝐇‖2𝐹。此外,‖𝐇‖𝜏具有良好的二微、非负、凸性质,有利于优化。因此,‖𝐡‖𝜏适用于损失函数,并通过调优𝜏对不同类型的异常值具有鲁棒性。
根据以上分析,在FKM算法(1)中引入了自适应损失函数(7),极大地提高了聚类的鲁棒性如下:
\[\begin{array}{l}{\operatorname*{min}\mathcal{L}(\mathbf{U},\mathbf{V})=\sum_{n=1}^{N}\sum_{c=1}^{C}u_{n
c}^{2}||\mathbf{x}_{n}-\mathbf{v}_{c}||_{\tau}}\\{\mathrm{s.t.}\quad\sum_{c=1}^{C}u_{n
c}=1,0\leq u_{n c}\leq1}\end{array}\]
3.2.对象的拉普拉斯正规化
图的拉普拉斯算子确保了从彼此连接的样本中学习到相似的隶属度。同时,它还可以利用数据的局部性信息。因此,我们将拉普拉斯正则化纳入聚类模型。它可以根据样本𝐱𝑖和𝐱𝑗之间的相似性来实现。我们使用热核方案[31]来构造相似度如下: \[s_{ij}=\begin{cases}e^{-\frac{\|\mathbf{x}_i-\mathbf{x}_j\|}{0.5}} & j\in NB_i \\0, & \mathrm{otherwise} & \end{cases}\] 其中,\(NB_i\)为𝑖th样本的邻域集。然后计算\(𝐒=(𝐒+𝐒^𝑇)/2\),得到对称相似矩阵。结合(8)和(9),我们可以得到以下模型: \[\mathcal{L}(\mathbf{U},\mathbf{V})=\sum_{n=1}^{N}\sum_{c=1}^{C}u_{n c}^{2}\left\|\mathbf{x}_{n}-\mathbf{v}_{c}\right\|_{\tau}+~\mu\sum_{c=1}^{C}\sum_{n=1}^{N}\sum_{j\in N B_{n}}s_{n j}(u_{n c}-u_{j c})^{2}\\{\mathrm{s.t.}}\;\sum_{c=1}^{C}u_{n c}=1,0\leq u_{n c}\leq1\]
3.3.RD-FKC算法
给定图像\(\{\bf
X_{n}\}_{n=1}^{N}\),编码器首先尝试提取层次特征,然后将图像映射到一个非线性嵌入空间,以获得潜在的潜在表示𝐙。相比之下,解码器会将该特征重构回原始图像中。
为了保证学习到的低维空间不被扭曲和破坏,RD-FKC模型结合了DCAE网络,将具有拉普拉斯正则化的鲁棒FKM损失函数嵌入到一个联合框架中,如下所示:
\[\operatorname*{min}_{A.\mathrm{U.V}}\quad{\frac{1}{N}}\sum_{n=1}^{N}\|{\hat{\mathbf{X}}}_{n}-\mathbf{X}_{n}\|_{F}^{2}+\sum_{n=1}^{N}\sum_{c=1}^{C}u_{n
c}^{2}\left\|\mathbf{z}_{n}-\mathbf{v}_{c}\right\|_{\tau}+~\mu\sum_{c=1}^{C}\sum_{n=1}^{N}\sum_{j\in
N B_{n}}s_{n j}(u_{n c}-u_{j
c})^{2}+\gamma\sum_{\ell=1}^{L}(\|\mathbf{W}^{(\ell)}\|_{F}^{2}+\|\mathbf{b}^{(\ell)}\|_{2}^{2})\\{\mathrm{s.t.}}\
\sum_{c=1}^{C}u_{n c}=1,0\leq u_{n c}\leq1\]
其中,𝜇和𝛾是权衡参数。建立RD-FKC模型可分为四个部分(11)。第一项是最小化重构误差,以确保潜在的表示法尽可能多地保留原始信息。第二项表示由嵌入空间中的嵌入特征和聚类中心组成的自适应损失函数的FKM。第三项是约束隶属度矩阵,使具有相似隶属度的样本点也更接近。第四项用于避免过拟合,防止网络产生平凡解。
3.4.最优化
在(11)中,RD-FKC通过使用结合\(\ell_{1}\)范数和\(\ell_{2}\)范数的自适应损失函数来计算聚类误差。为了解决这个问题,我们首先考虑一个一般损失函数定义为: \[\operatorname*{min}_{\mathbf{x}}g(\mathbf{x})+\sum_{i}{\frac{(1+\tau)\|d_{i}(\mathbf{x})\|_{2}^{2}}{\|d_{i}(\mathbf{x})\|_{2}+\tau}}\] 其中,\(d_{i}(\mathbf{x})\)为向量输出。受[29,32]的启发,采用了一种迭代重加权的方法来求解它。通过对𝐱进行(12)的导数并将其设为零,我们得到 \[g^{\prime}({\bf x})+2(1+\tau)\sum_{i}\frac{\|d_{i}({\bf x})\|_{2}+2\tau}{2(\|d_{i}({\bf x})\|_{2}+\tau)^{2}}d_{i}({\bf x})d_{i}^{\prime}({\bf x})=0\] 定义 \[k_{i}=(1+\tau)\frac{\|d_{i}({\bf x})\|_{2}+2\tau}{2(\|d_{i}({\bf x})\|_{2}+\tau)^{2}}\] 然后是等式(13)可以重写为 \[g^{\prime}({\bf x})+2\sum_{i}k_{i}d_{i}({\bf x})d_{i}^{\prime}({\bf x})=0\] 需要注意的是,𝐾𝑖的值依赖于𝐱,当𝑘𝑖被固定时,(12)中的问题等于 \[\operatorname*{min}_{\mathbf{x}}g(\mathbf{x})+\sum_{i}k_{i}\|d_{i}(\mathbf{x})\|_{2}^{2}\] 在[29]中证明了上述优化问题的收敛性。则(11)中的模型可以重新表述为: \[\operatorname*{min}_{A.\mathrm{U.V}}\quad{\frac{1}{N}}\sum_{n=1}^{N}\|{\hat{\mathbf{X}}}_{n}-\mathbf{X}_{n}\|_{F}^{2}+\sum_{n=1}^{N}\sum_{c=1}^{C}u_{n c}^{2}k_{n c}\left\|\mathbf{z}_{n}-\mathbf{v}_{c}\right\|_{\tau}\\+~\mu\sum_{c=1}^{C}\sum_{n=1}^{N}\sum_{j\in N B_{n}}s_{n j}(u_{n c}-u_{j c})^{2}+\gamma\sum_{\ell=1}^{L}(\|\mathbf{W}^{(\ell)}\|_{F}^{2}+\|\mathbf{b}^{(\ell)}\|_{2}^{2})\\{\mathrm{s.t.}}\ \sum_{c=1}^{C}u_{n c}=1,0\leq u_{n c}\leq1\] 其中 \[k_{n c}=(1+\tau)\frac{\|\mathbf{z}_{n}-\mathbf{v}_{c}\|_{2}+2\tau}{2(\|\mathbf{z}_{n}-\mathbf{v}_{c}\|_{2}+\tau)^{2}}\] 可以看出,在模型(17)中有三个变量,很难直接解决这些问题。因此,我们提出了一个迭代的替代策略来优化它。

4.实验结果及分析
在本节中,所提出的RD-FKC模型的性能估计是基于8个图像集,使用三个公共指标,包括准确率(ACC)、归一化互信息(NMI)和纯度(Pur)。为了评估RD-FKC的能力,我们将其与现有的聚类技术进行了比较,如𝐾-means聚类(KM)[3]、模糊𝐾-means聚类(FKM)[4]、RSFKM
[34],PCAKM,深度嵌入式聚类(DEC)[22],深度聚类网络(DCN)[35]和深度模糊𝐾-means(DFKM)[36]。
在接下来的章节中,我们首先列出图像数据集的特征,然后给出实验实现的细节。此外,我们还报告了RD-FKC与其他方法相比的性能。最后,分析了各参数的灵敏度。
4.1.数据集
实验中使用了八种不同类型的图像集,包括人脸、手写数字、物体和时尚数据集。表2详细描述了这些图像集的特征,图2显示了我们实验中的几个样本。

人脸上包括Jaffe、Yale、ORL和CMU-PIE。Jaffe包含213个26个×26的样本,来自10个人,有7种不同的表达。Yale有165张32张×32像素的图像。ORL由40人在不同光照条件下的400张图像组成。CMU-PIE由64人的32×32像素的图像组成。USPS是一个手写的数字数据集,包括9298个16×16像素的样本。对象数据库包含COIL20,128个×128像素的20个对象,CIFAR10包含60 000的10类彩色图像。Fashion-MNIST是MNIST的替代品,包括10个类别的70 000张时尚产品图片。
4.2.网络设置
4.3.聚类结果的比较
4.4.对鉴别力和表现形式的可视化
4.5.参数分析
5.结论
在这项工作中,我们提出了一种新的称为鲁棒深度模糊𝐾-means聚类(RD-FKC)的框架,该框架利用拉普拉斯正则化来保持输入图像的局部结构,并使用自适应损失函数通过调整𝜏来提高聚类模型的弹性。RD-FKC通过将DCAE和聚类模型整合到一个联合框架中,充分利用DCAE学习图像的判别和深度表示,然后进行鲁棒聚类,有助于解决图像聚类问题。此外,还提出了一种有效、实用的模型优化算法。在不同图像集上进行的大量可比实验表明,RD-FKC优于现有的传统和深度聚类方法。
可以观察到,RD-FKC在CIFAR10等彩色图像上表现不佳。可能的原因是局部结构信息没有得到有效的保存。因此,在今后的工作中,我们将考虑将𝑝-拉普拉斯正则化技术[39]嵌入到聚类模型中,从而更好地实现局部信息的保存。由于引入了一个额外的超参数𝑝,我们将进一步考虑集成𝑝-拉普拉斯正则化[40],它对各种𝑝值图应用适当的权值,以更好地理解数据的几何形状。此外,我们还将考虑如何设计一个更先进的深度卷积自动编码器网络来提取特征,从而进一步提高聚类效率。
6.代码结构
https://github.com/soft-clustering/soft-clustering/blob/main/docs/source/rdfkc.md |
代码的总体结构按照编码器-解码器的自编码器的结构
self.Z = self.encoder(self.X) |
所以也有基于存在重构x的过程。
构建隶属度矩阵U、聚类中心V、相似度矩阵S的初始化:
self.U = self._initialize_membership_matrix() |
然后再迭代中优化模型参数、聚类中心和隶属度矩阵:
for _ in range(self.max_iter): |
最后输出隶属度矩阵U作为最后的结果:
torch.argmax(self.U, dim=1).numpy() |
6.1优化模型参数函数
\[{\mathcal{L}}(\Delta)={\frac{1}{N}}\sum_{n=1}^{N}\|{\hat{\mathbf{X}}}_{n}-\mathbf{X}_{n}\|_{F}^{2}+\sum_{n=1}^{N}\sum_{c=1}^{C}u_{n c}^{2}k_{n c}\|\mathbf{z}_{n}-\mathbf{v}_{c}\|_{2}^{2}+\gamma\sum_{\ell=1}^{L}(\|W^{(\ell)}|_{F}^{2}+\|\mathrm{B}^{(\ell)}\|_{2}^{2})\]
使用计算x与x_recon的重构损失 $ {}{n=1}^{N}|{}{n}-{n}|{F}^{2} $
recon_loss = F.mse_loss(self.X_recon, self.X) |
由嵌入空间中的嵌入特征和聚类中心组成的自适应损失函数
\[\sum_{n=1}^{N}\sum_{c=1}^{C}u_{n c}^{2}\left\|\mathbf{z}_{n}-\mathbf{v}_{c}\right\|_{\tau}+~\mu\sum_{c=1}^{C}\sum_{n=1}^{N}\sum_{j\in N B_{n}}s_{n j}(u_{n c}-u_{j c})^{2}\]
cluster_loss = 0.0 |
约束隶属度矩阵 \[\gamma\sum_{\ell=1}^{L}(\|\mathbf{W}^{(\ell)}\|_{F}^{2}+\|\mathbf{b}^{(\ell)}\|_{2}^{2})\]
reg_loss = 0.0 |
其中:
def _compute_ki(self, dist: float) -> float: |
6.2更新聚类中心
基于以下公式更新: \[\mathbf{v}_{c}={\frac{\sum_{n=1}^{N}\,k_{n c}u_{n c}^{2}\mathbf{z}_{n}}{\sum_{n=1}^{N}\,k_{n c}u_{n c}^{2}}}\]
def _update_cluster_center_matrix(self) -> None: |
6.2更新隶属度矩阵
基于以下公式更新隶属度矩阵: \[u_{nc}=\frac{p_{nc}+\frac{2-\sum^C_{c=1}\frac{p_nc}{q_nc}}{\sum^C_{c=1}\frac{p_nc}{q_nc}}}{2q_{nc}}\]
def _update_membership_matrix(self) -> None: |