SPL
多任务网络上的分布式安全聚类与估计
摘要
近年来,分布式安全估计问题得到了广泛的研究。然而,在多任务网络中,恶意信息和任务之间的不确定关系对现有的相关算法提出了挑战。为了获得可靠的估计,提出了分布式安全聚类和估计(DSCE,Distributed Secure Clustering and Estimation)算法。该算法包括一个具有自适应组合系数的扩散滤波器,以及一个维数检测器。通过估计节点间的最大任务间间隙,完成了恶意信息的自适应区分过程。此外,提出了安全聚类方案,通过根据检测结果动态采用防御策略来减轻攻击者的影响。仿真结果证明了该算法对攻击的鲁棒性。
I.介绍
分布式参数估计问题近年来得到了广泛的讨论。目标是基于分布在网络中的节点集合的测量值和回归向量来近似最优估计。这些节点与相邻节点进行协同估计,以提高结果的准确性。此外,还确定了三种主要的协作方法:增量方法[1]、共识方法[2]和扩散方法[3]。其中,扩散方法被认为是最突出的。
当考虑到网络攻击的存在时,来自节点的数据通常是伪造的,从而导致估计过程的中断。因此,没有适当防御机制的算法通常会导致性能下降。为了解决这一挑战,我们提出了各种安全估计算法,如:[4]-[9]所示。在[4]中,采用了一种基于声誉的检测器来识别恶意传感器。在[5]、[6]中,Hua等人分别设计了一种基于kl-发散的检测机制和交叉验证方法来区分被攻击的节点。在[9]中,建立了一个参考子系统来检测恶意信息,并提供可靠的替换信息。此外,一些研究也关注于多任务场景下的问题。在[10]中,Wang等人提出了一种基于贝叶斯的估计器来在多任务对抗网络中获得可靠的估计。在[11]中,实现了局部-离群值-因子(LOF,Local-Outlier-Factor)来测量和定位多任务环境下的恶意估计。
上述研究为解决单任务和多任务环境下的安全估计问题做出了贡献。然而,很少有研究考虑先前聚类信息不可用的多任务环境,这在实际应用中是一个更普遍和具有挑战性的场景。
值得注意的是,在多任务网络中,集群信息的不确定性导致节点之间的协作不协调,导致相关算法的性能下降。此外,任务间邻居之间未知的内在差异混淆了检测过程,从而增加了区分被攻击节点的难度。
本文主要考虑了FDI攻击和部分FDI攻击的存在性,并提出了分布式安全聚类和估计(DSCE)算法。在该算法中,通过具有自适应组合系数的扩散滤波器([12]中的AC-dLMS滤波器),得到了一个锚定估计,作为可靠的参考。通过对锚定估计的维数检测过程,识别出可靠的数据。此外,还设计了一种自适应更新节点阈值的方法,基于评估任务间间隙造成的最大差异。随后,采用了安全聚类方案。通过根据检测结果选择不同的防御策略,在聚类过程中拒绝恶意信息。最后,将来自安全簇内邻居的中间估计结合在一起以获得安全估计。仿真结果表明,该算法在抑制FDI攻击和部分FDI攻击方面是可行的。
II.准备工作
本节分别简要介绍了在无攻击环境下的多任务扩散LMS(multi-dLMS)算法和攻击模型。
A. 多任务环境下的扩散LMS算法
本文简要考虑了一个具有N个节点的多任务模型,并将其划分为Q个簇。
在每个时刻t,每个节点接收到\(\{d_{k,t},\mathbf{u}_{k,t}\}\),其中\(d_{k,t}\)表示标量测量值,\(\mathbf{u}_{k,t}\)表示一个L维的输入回归向量。特别是它们之间的线性关系如下:
\[d_{k,t}=\mathbf{u}_{k,t}^{T}\mathbf{w}_{k}^{o}+v_{k,t},\]
其中\(\mathbf{w}_{k}^{o}\)是节点k的未知l维最优估计,\(v_{k,t}\)是噪声项。
不同集群之间的关系表示如下:
\[\begin{array}{ll}\mathbf{w}_{k}^{o} =
\mathbf{w}_{C(q)}^{o}, & \text{if } k \in \cal C(q);
\\\mathbf{w}_{C(p)}^{o} = \mathbf{w}_{C(q)}^{o}, & \text{if } \cal
C(p) \text{ and } \cal C(q) \text{ are connected;}\end{array}\]
其中,\(\mathbf{w}_{C(q)}^{o}\)为第p个簇中节点的索引集。
主要目标是通过与邻居通信来近似最近的最优估计。本部分主要讨论了采用适应后再组合(ATC,adapt-then-combine)策略的多任务dLMS算法。这些方程式说明如下:
\[\varphi_{k,t}={\bf
w}_{k,t-1}+\mu_{k}\sum_{\ell\in{\cal N_{k}}\cap{\cal
C}_{k}}[\cal{c}_{\ell,t}(d_{\ell,t}-{\bf u}_{\ell,t}^{T}{\bf
w}_{k,t-1})]\]
\[{\bf w}_{k,t}=\sum_{\ell\in{\cal N_{k}}\cap{\cal C}_{k}}a_{\ell,k}\varphi_{k,t},\]
其中\(\varphi_{k,t}\)和\(\mathbf{w}_{k\cdot t}\)分别为节点k在时间t时的中间估计和瞬时估计,\(\mu_k\)为步长,\({\cal N}_{k}\)为节点k的邻居集合,\({\cal C}_{k}\)为节点k所属的聚类集合。非负系数\(a_{\ell,k}\)、\(c_{\ell,k}\)分别为左随机矩阵A和右随机矩阵C的\((\ell,k)\)级别实体,即: \[\mathbf{A}^{T}\mathbf{1}_{N}=\mathbf{1}_{N},a_{\ell,k}=0\;\mathrm{if}\;\ell\not\in\mathcal{N}_{k},\]
\[\mathrm{C1}_{N}\,=\,{\bf1}_{N},c_{\ell.k}\,=\,0\mathrm{~if~}\ell\not\in\mathcal{N}_{k},\]
其中,\({\bf1}_{N}\)表示带有单位项的列向量。
B.攻击模型
本文考虑了FDI攻击和部分FDI攻击,具体如下所示:
1) FDI攻击
对于FDI攻击,注入恶意信息篡改每个节点的测量值\(d_{k,t}\),如下: \[\tilde{d}_{k,t}\,=\,d_{k,t}\,+\,d_{k,t}^{a t t},\] 其中\(\tilde{d}_{k,t}\)是受损的测量值,\(d_{k,t}^{a t t}\)是一个标量,满足: \[d_{k,t}^{a t t}=\mathbf{u}_{k,t}^{T}\mathbf{p}_{k}\] 其中\(\mathbf{p}_{k}\)是一个被攻击节点的l维非零向量,而是一个普通节点的零向量。
2)部分FDI攻击
部分FDI攻击是FDI攻击的一种特例。由于网络内的攻击强度和范围降低,对攻击者更隐蔽和高效。
类似地,部分FDI攻击者向被攻击的节点发送满足(7)和(8)的恶意信息。然而,只有部分L维的估计是证伪的,这可以显示为:\(0\lt \|\mathbf{q}_{k}\|_{0}\lt
L\)。
此外,在我们所考虑的对抗性环境中,假设在[4]-[6],[9]-[11]中所采用的假设如下。
假设1:被攻击的节点数小于\([{\frac{|N_{k}|}{2}}]\)。
III.分布式安全聚类与估计算法
在本部分中,提出了DSCE算法来在存在攻击的情况下产生安全的聚类和估计结果。从系统学的角度来看,采用了AC-dLMS滤波器。从实现的角度来看,主要包括四个主要步骤:自适应、检测、聚类和组合。在下面的几个部分中,我们将简要地描述这些过程。
A.自适应
在这一步中,基于\(\{d_{k,t},\mathbf{u}_{k,t}\}\),每个节点调整中间估计值\(\varphi_{k,t}\)如下: \[\varphi_{k,t}=\psi_{k,t-1}+\mu_{k}\sum_{\ell\in{N_{k}}}c_{\ell,k}{\mathbf{u}}_{\ell,i}(d_{\ell,i0}-{\mathbf{u}}_{\ell,i}^{T}\psi_{k,t-1})\]
其中,\(\psi_{k,t-1}\)表示节点k在t-1时刻的另一个中间估计值。
组合系数\(a_{\ell,k}\)、\(c_{\ell,k}\)可以根据任务间的相似性进行调整。因此,具有异常估计的恶意节点可以被未受攻击的节点自适应地隔离。此外,利用邻居之间的协作可以获得更准确的估计。因此,与非合作滤波器相比,AC-dLMS滤波器更有效。
B.检测
在这一步中,获得排除恶意信息的锚点估计\({\tilde{\mathbf{w}}}_{k,i}\)以供参考。具体建立了节点k的第m维的排序序列如下:
\[\boldsymbol{\Phi}_{k,t}^{(m)}=\{\varphi_{\ell_{1},t}^{(m)},...,\varphi_{\ell_{s},t}^{(m)},...,\varphi_{\ell_{n_k},t}^{(m)}\}\]
其中\(\varphi_{\ell_{1},t}^{(m)}<\varphi_{\ell_{s},t}^{(m)}<\varphi_{\ell_{n_k},t}^{(m)}\)和\(\ell_{1},\ell_{s},\ell_{n_{k}}\in{\cal
N}_{k}\)。
根据假设1,攻击者倾向于使数据偏离之前的值。因此,当节点k及其相邻节点按估计值进行排序时,被攻击的节点更有可能位于被排序序列的左侧或右侧。因此,中心中的值通常比其他值更可靠,可以被认为是锚定估计的元素。
因此,可以建立锚定估计中节点k的第m维估计:
\[\bar{\mathbf{w}}_{k,t}^{(m)}=\boldsymbol{\Phi}_{\lceil\frac{|\mathcal{N}_k|}{2}\rceil,i}^{(m)}.\]
由于得到了每个节点的可靠估计,因此设计了一个基于阈值测试过程的维数攻击检测器来定位可靠的信息。
具体来说,对于节点k的第m个维数,如果中间估计\(\varphi_{k,t}\)和锚估计\(\mathbf{\bar
w}_{k,t}\)之间的距离超过阈值,可以推断维数受到攻击,反之亦然。判断过程表现如下:
\[\|\bar{\mathbf{w}}_{k,t}^{(m)}-\varphi_{k,t}^{(m)}\|^2\overset{\mathbb{H}_1}{\underset{\mathbb{H}_2}{\lessgtr}}b\cdot\theta_{k,t},\]
\[\theta_{k,t}=\begin{cases}\epsilon_k, & \mathrm{if}\epsilon_k>\theta_{k,t-1}; \\\theta_{k,t-1}, & \mathrm{otherwise}, & \end{cases}\]
\[\epsilon_{k}=\|m a x\{\bar{\bf w}_{k,t}^{(m)}-\bar{\bf w}_{\ell,i}^{(m)}|\ell\in\mathcal{N}_{k}\|^{2}\]
其中,\(\theta_{k,t}\)为自适应阈值,视为由任务间差异引起的节点之间的最大距离,更新公式在(13)和(14)中。此外,b是一个预定义的常数,用于调整判断条件的松弛或紧性,H1和H2分别是节点k的第m维估计是安全的和被攻击的假设。
此外,以下变量用于记录检测结果:
\[T_{m,k}=\begin{cases}1, &
\mathrm{if}~\mathbb{H}_1\text{is achieved}; \\0, &
\mathrm{if}~\mathbb{H}_2\text{is achieved}; &
\end{cases}\]
\[s_{k}={\left\{\begin{array}{l l}{1,}&{\mathrm{if~}\|\mathbf{T}_{k}\Vert_{1}^{1}=L;}\\ {0,}&{\mathrm{otherwise;}}\end{array}\right.}\]
其中\({\bf T}_{k}=\{T_{1,k},T_{2,k},\ldots,T_{L,k}\}^{T}\)。
C. 聚类
在这一步中,通过以下自适应聚类方案更新系数\(a_{\ell,k}\)和\(c_{\ell,k}\)的值,完成了AC-dLMS滤波器的聚类过程: \[a_{\ell,k}={\frac{\|\varphi_{k,\ell}+\mu_{k}{\bf q}_{k,\ell}-\varphi_{\ell,\imath}\|^{-2}}{\sum_{j\in{\cal N}_{k}}\|\varphi_{k,\ t}+\mu_{k}{\bf q}_{k,\ t}-\varphi_{j,\imath}\|^{-2}}}\]
\[c_{k,\ell}=a_{\ell,k}\]
其中\({\bf q}_{k,t}={\bf
u}_{k,t}(d_{k,t}-{\bf
u}_{k,t}^{T}\varphi_{k,t})\)。
因此,对于节点k,估计值相似性较高的邻居赋值越大,在每个信息融合过程中占越大的影响。
同样,在该算法中,也可以通过调节系数\(\tilde{a}_{\ell,k}\)来消除恶意信息的影响。因此,提出了安全聚类方案。在该方案中,根据检测结果,动态地采用了防御策略。
1)情形1
当\(\|\mathbf{T}_{k}\|_{1}^{1}=L\)时,节点k状态为安全。此外,恶意节点被\(a_{\ell,k}\)排除,因此,没有必要采取其他措施,我们设置: \[\check{a}_{\ell,k}=a_{\ell,k}\]
2)情形2
当\(0<\|\mathbf{T}_{k}\|_{1}^{1}<L\)时,表示节点k受到部分攻击。因为可以利用来自未受攻击的维数的信息来判断节点之间的相似性。因此,提出了自适应部分聚类(APC,Adaptive
Partial Clustering)算法来恢复聚类信息。
首先,利用\(\mathbf{T}_{k}\)对Hadamard积的尺寸级异常信息进行过滤,生成部分型安全信息如下:
\[\dot{\varphi}_{\ell.i}=\varphi_{\ell.i}\odot\mathbf{T}_{k},\ell\in{\mathcal{N}}_{k},\]
\[{\dot{\mathbf{q}}}_{k,t}=\mathbf{u}_{k,t}(d_{k,t}-\mathbf{u}_{k,t}^{T}{\dot{\varphi}}_{k,t})\]
然后,生成\({\check{a}}_{\ell,k}\)如下: \[\check{a}_{\ell,k}=\frac{s_{\ell}\cdot\|\dot{\varphi}_{k,t}+\mu_{k}\dot{\bf
q}_{k,t}-\dot{\varphi}_{\ell,i}\|^{-2}}{\sum_{j\in
N_{k}}s_{j}\cdot\|\dot{\varphi}_{k,t}+\mu_{k}\dot{\bf
q}_{k,t}-\dot{\varphi}_{j,i}\|^{-2}}\] 其中,\(s_j\)用于过滤异常节点。
在得到\({\check{a}}_{\ell,k}\)后,其安全的簇内邻居通过组合步骤可以恢复被攻击节点的错误估计。
3)情形3
当\(\|\mathbf{T}_{k}\|_{1}^{1}\ =\ 0\)时,节点k被认为受到FDI攻击者的影响。在这种情况下,将无法恢复聚类信息。此外,也没有可用的资料来替代受攻击的估计数。因此,将去掉节点k,以减轻其对网络的影响。
D. 组合
当前一个步骤完成后,计算出组合系数\(a_{\ell,k}\)和\({\check{a}}_{\ell,k}\)。因此,在这一步中,每个节点组合了该步骤中来自其邻居的中间估计。
对于AC-dLMS滤波器,估计值\(\psi_{k,i}\)的计算方法如下: \[\psi_{k,t}=\sum_{\ell\in{\cal
N}_{k}}a_{\ell,k}\varphi_{k,t}\] 可靠的瞬时估计\(\mathbf{w}_{k,t}\)生成为: \[\mathbf{w}_{k,t}=\sum_{\ell\in {\cal
N}_{k}}{\check{a}}_{\ell,k}\varphi_{k,t}\]
综上所述,在算法1中总结了该算法的更新过程。
算法1:DSCE算法
- 初始化:Let \(\mathrm{w}_{k,0}=\psi_{k,0}=\varphi_{k,0}=0\)。
2. for t=1 to T do
3. for k=1 to N do
4. 公式(9)中的自适应中间估计 \(\varphi_{k,t}=\psi_{k,t-1}+\mu_{k}\sum_{\ell\in{N_{k}}}c_{\ell,k}{\mathbf{u}}_{\ell,i}(d_{\ell,i0}-{\mathbf{u}}_{\ell,i}^{T}\psi_{k,t-1})\)
5. 获得公式(10)、公式(11)的锚定估计 \(\bar{\mathbf{w}}_{k,t}^{(m)}=\boldsymbol{\Phi}_{\lceil\frac{|\mathcal{N}_k|}{2}\rceil,i}^{(m)}\) \(\boldsymbol{\Phi}_{k,t}^{(m)}=\{\varphi_{\ell_{1},t}^{(m)},...,\varphi_{\ell_{s},t}^{(m)},...,\varphi_{\ell_{n_k},t}^{(m)}\}\)
6. 检测信任维度并获取\({\bf T}_{k}\) \(T_{m,k}=\begin{cases}1, & \mathrm{if}~\mathbb{H}_1\text{is achieved}; \\0, & \mathrm{if}~\mathbb{H}_2\text{is achieved}; & \end{cases}\)
7. 执行自适应聚类方案,得到\(a_{\ell,k}\)和\(c_{\ell,k}\) \(a_{\ell,k}={\frac{\|\varphi_{k,\ell}+\mu_{k}{\bf q}_{k,\ell}-\varphi_{\ell,\imath}\|^{-2}}{\sum_{j\in{\cal N}_{k}}\|\varphi_{k,\ t}+\mu_{k}{\bf q}_{k,\ t}-\varphi_{j,\imath}\|^{-2}}}\) 、\(c_{k,\ell}=a_{\ell,k}\)
8. 如果\(\|\mathbf{T}_{k}\|_{1}^{1}=L\)
9. 设置\(\check{a}_{\ell,k}=a_{\ell,k}\)
10. 如果\(0<\|\mathbf{T}_{k}\|_{1}^{1}<L\)
11. 设置\(\check{a}_{\ell,k}=\frac{s_{\ell}\cdot\|\dot{\varphi}_{k,t}+\mu_{k}\dot{\bf q}_{k,t}-\dot{\varphi}_{\ell,i}\|^{-2}}{\sum_{j\in N_{k}}s_{j}\cdot\|\dot{\varphi}_{k,t}+\mu_{k}\dot{\bf q}_{k,t}-\dot{\varphi}_{j,i}\|^{-2}}\)
12. 否则删除节点k
13. 结合中间估计,分别得到\(\psi_{k,i}\)和\(\mathbf{w}_{k,t}\)。 \(\psi_{k,t}=\sum_{\ell\in{\cal N}_{k}}a_{\ell,k}\varphi_{k,t}\) \(\mathbf{w}_{k,t}=\sum_{\ell\in {\cal N}_{k}}{\check{a}}_{\ell,k}\varphi_{k,t}\)
IV.模拟
在本节中,我们考虑了一个包含5个不同集群的21个节点的多任务网络,其拓扑结构如图1 (a)所示。
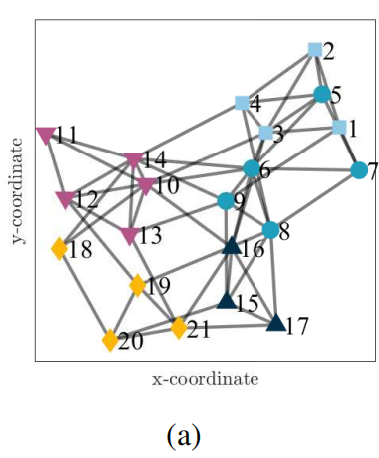
具体而言,\(\mathcal{C}_{1}=\{1,2,3,4\}\),\(\mathcal{C}_{2}=\{5,6,7,8,9\}\),\(\mathcal{C}_{3}=\{10,11,12,13,14\}\),\(\mathcal{C}_{4}=\{15,16,17\}\),\(\mathcal{C}_{5}=\{18,19,20,21\}\)。输入信号\(\mathbf{u}_{k,t}\)和噪声项\({v}_{k,t}\)均被视为零均值高斯随机变量,其方差为\(\sigma_{u,k}^{2}\)和\(\sigma_{v,k}^{2}\),如图1 (b)所示。\(\mathbf{w}_{k}^{o}\)的尺寸设置为:\(L=5\)。
为了进行比较,本文还说明了[13]中的多dLMS算法、nc-LMS算法、[12]中的AC-dLMS算法以及[9]中的S-dLMS算法的曲线。此外,在图例中用星号标记的项目表示已经给出了聚类信息。
A.示例1
在第一个例子中,在网络中只考虑了部分的FDI攻击。具体来说,被攻击节点的集合为\(\{2,13,19\}\)。相应估计的前两个维度是受到部分FDI攻击。
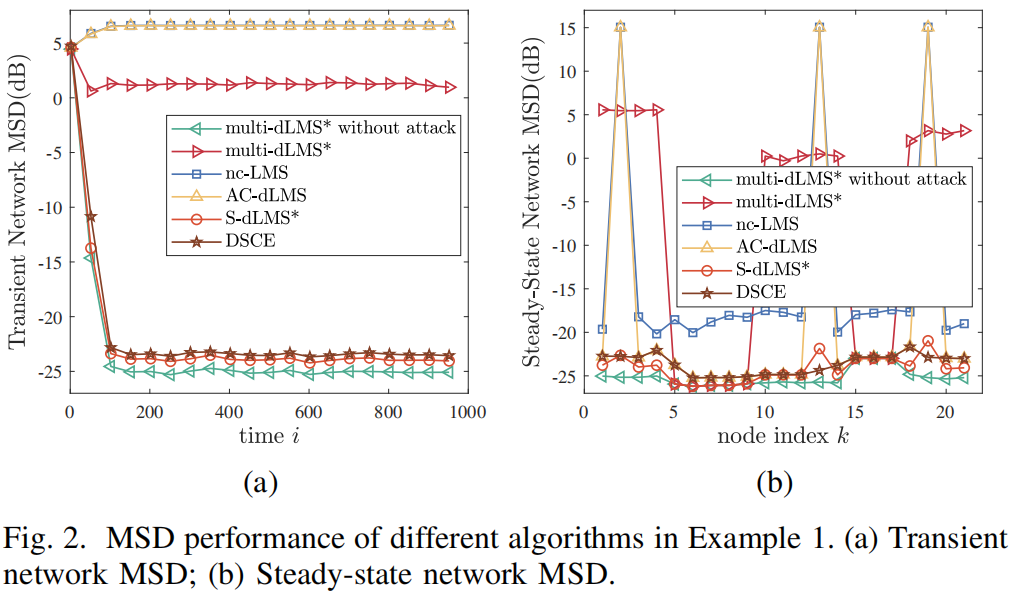
图2
(a)给出了不同算法的瞬态MSD曲线。在存在攻击的情况下,DSCE算法表现出良好的性能,几乎达到了与无攻击的S-dLMS*和多dLMS算法相同的性能。计算结果表明,该算法已经完成了安全的聚类和估计任务。特别是,即使没有任务间关系的先验信息,该算法也获得了与与聚类信息相关的算法几乎相同的精度。
从图2
(b)中的稳态MSD曲线可以看出,被攻击节点的估计值被其任务对应的安全值所取代。
此外,与nc-LMS算法相比,AC-dLMS算法的未攻击节点具有较低的稳态MSD值,说明AC-dLMS滤波器在获得更准确的锚定估计方面具有优越性。
B.示例2
为了验证该算法在更复杂的攻击环境下的鲁棒性,在示例2中考虑了这两种类型的攻击。具体来说,节点10和21受到FDI攻击,节点1和5受到部分FDI攻击,相应的前三个维度被篡改。
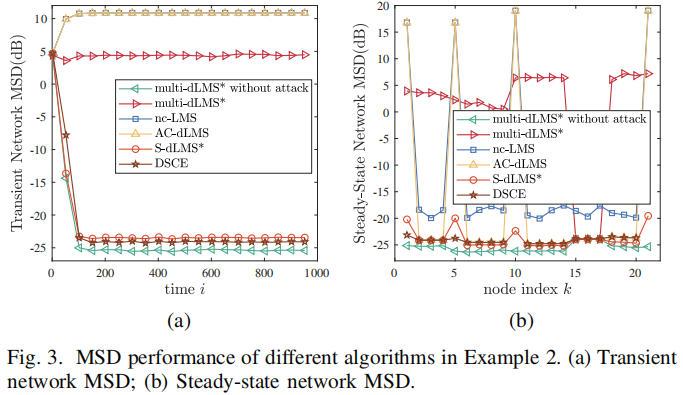
不同算法的瞬态MSD曲线如图3
(a)。所示得到了与示例1相似的结果,证明了其对攻击的鲁棒性。
从图3
(b)可以看出,在该算法中,受FDI攻击的节点被删除,而受部分FDI攻击的节点被其安全的簇内邻居恢复。结果表明,该检测器在区分攻击方面的可靠性和安全聚类方案在消除攻击者影响方面的有效性。
综上所述,这两个实例都证明了该算法在攻击下是有效的。
V.结论
为了获得存在网络攻击情况下的安全估计,本文引入了DSCE算法。该算法采用了一种具有自适应协同系数的扩散滤波器。伴随着具有自适应阈值的维级攻击检测器,可以更准确地定位恶意信息。此外,还提出了安全聚类方案来消除恶意信息的影响。最后,通过融合邻居的任务内安全估计,得到了可靠的估计。仿真结果表明,该算法在抵御FDI攻击和部分FDI攻击方面是有效的。
评审:
对比论文一
Secure Distributed Estimation Over Wireless Sensor Networks Under Attacks
初步和问题制定
无攻击的扩散LMS
受攻击下的安全分布式估计