Towards Generalizable Detector for Generated Image
Towards Generalizable Detector for Generated Image
Qianshu Cai1 ,Chao Wu2,3
,Yonggang Zhang4 ,Jun Yu5
,Xinmei Tian1
∗
1中国科学技术大学教育部脑科学智能感知与认知重点实验室,
2浙江大学
3河北通信学院人工智能学院
4香港科技大学
5哈尔滨工业大学深圳校区智能科学与工程学院
摘要
有效检测生成图像对于防范其滥用风险至关重要。尽管已取得显著进展,但一个根本性挑战依然存在:如何确保检测器的泛化能力。为此,我们提出一种受人类认知机制启发的全新视角来理解和改进生成图像检测技术——人类通过识别特定模式来判断图像是否自然,因为这些模式超出了自然图像特征的范畴。这本质上与分布外(OOD)检测相关,该检测方法通过识别语义模式(即标签)超出分布内(ID)样本语义模式空间的样本来实现。通过将生成图像的模式视为 OOD 样本,我们证明了仅在自然图像上训练的模型,在轻度假设条件下即可保证泛化能力。这一方法将生成图像检测的泛化挑战转化为自然图像模式的拟合问题。基于此洞见,我们通过ID能量的视角提出了一种可泛化的检测方法。理论结果揭示了该方法的泛化风险,而多项基准测试的实验结果充分证明了我们方法的有效性。代码可在 https://github.com/dav-joy-thon/DEnD-Detection 上找到。
1.引言
近年来,生成式人工智能领域取得了重大突破。特别是基于扩散模型的生成技术[22,44,10,56]在图像合成领域展现出革命性进展。包括Stable
Diffusion[56]、DALL-E
3[50]、Midjourney[41]和FLUX[29]在内的先进生成模型,让用户只需简单输入文本提示即可生成高度逼真的图像。更值得一提的是,视频生成领域的明星产品Sora[47]不仅能制作高清逼真视频,还能模拟真实物理效果。然而,这种技术的迅猛发展也暗藏风险与挑战。恶意分子滥用生成图像进行欺诈行为,已引发人们对媒体信息真实性的质疑。因此,开发具备强大泛化能力的有效生成图像检测系统,以应对这些新兴威胁,显得尤为重要。
在生成图像检测领域,现有方法大多依赖训练二元分类器[69,68,64]。例如,DIRE[69]采用扩散重建误差作为指标训练二元分类器。而aeroblade[55]则提出了一种无需训练的方案,通过利用自动编码器的重建误差来检测由潜在扩散模型(LDM)[56]生成的图像。不过该方法存在局限性:只能识别
LDM
生成的图像,且需要获取用于图像生成的自动编码器。然而,这些方法面临着一个根本性挑战:如何确保所构建检测器的泛化能力。在实际应用中,我们经常遇到底层架构未知的生成模型,这使得泛化能力的挑战尤为突出。
为应对泛化挑战,我们重新审视人类识别生成图像的过程。仅接触过自然图像的人类,能够通过独特特征辨别生成图像。这可能源于人类感知到生成图像的模式存在于自然图像模式所覆盖空间之外。从这个角度看,这种“空间外操作”同样适用于检测分布外(OOD)数据。具体而言, OOD 检测器需要识别具有语义模式(即标签)的样本,这些样本位于分布内(ID)样本语义模式空间之外。人类识别生成图像的过程与分布外(OOD)检测原理[73]高度契合——人类仅接触过自然图像(ID)却能识别生成图像(OOD),而模型仅接触过ID样本却能检测 OOD 样本。这引发了一个基础却鲜少被探讨的问题:仅接触过自然图像的模型能否用于检测生成图像?
本研究提出一个创新视角:通过 OOD 检测的视角审视生成图像检测。在此框架下,自然图像的特征模式被视为ID数据,而生成图像的特征模式则属于 OOD 数据。基于 OOD 检测的可学习性理论[12],我们研究了生成图像检测的泛化能力,证明在温和假设条件下,基于自然图像训练的模型能确保生成图像检测的泛化能力。然而,生成图像检测依赖于特定特征模式的非重叠空间,而 OOD 检测则聚焦于ID与 OOD 数据语义标签的非重叠空间。具体而言, OOD 检测可利用基于ID数据标签空间训练的分类器,但生成图像检测无法使用针对语义标签训练的分类器。
为应对这一挑战,我们从基于密度和能量的 OOD 检测方法中汲取灵感。这些方法揭示了ID数据的能量(密度)低于(高于)OOD 数据的特性,这是因为模型在训练过程中会优先最小化(最大化)ID数据的能量(密度)。因此,我们沿用前人研究思路,重新定义生成图像检测中ID数据的能量指标。受[61]开创性研究启发,我们发现DINOv2[48]等自监督模型具备潜在能力(附录A中对此见解进行了详细说明)——能够识别生成图像与自然图像之间的模式差异。理论研究表明,自监督模型[34]的核心学习目标本质上是最小化ID数据(即自然图像)的差异能量评分。基于这一洞见,我们提出了一种名为差异能量检测(DEnD,differential energy-based detection)的创新框架,通过预训练自监督模型来识别生成图像,该框架展现出强大的泛化能力。
大量实验表明,我们的方法相较于基于训练的方法[69,68,64]具有更强的泛化能力,并且优于当前最先进的(SOTA)无训练方法。我们的主要贡献可归纳如下:
- 我们提出一种创新视角,通过将自然图像模式视为ID数据、生成图像模式视为 OOD 数据,来理解和改进生成图像检测。在此框架下,我们证明在自然图像上训练的模型,在温和假设条件下,能够确保生成图像检测的泛化能力。
- 本研究以能量基 OOD 检测为灵感,提出一种名为差异能量检测(DEnD)的创新框架,用于鉴别生成图像,并从理论上保证其泛化能力。
- 综合实验结果表明,我们的DEnD框架不仅超越了无需 SOTA 训练的方法,还优于大多数基于训练的检测器。此外,当面对Sora等无法访问的生成模型时,我们的方法展现出显著的泛化能力。
2.相关工作
高级图像生成模型
近年来,生成模型因其能生成高质量合成图像而备受关注。生成对抗网络(GANs)[16,2,26,24]为图像生成奠定了基础。生成对抗网络(GANs)问世后,基于扩散的生成技术[22,44,10]在图像合成领域取得革命性突破。近期的先进生成模型如Stable
Diffusion[56]、DALL-E
3[50]、Midjourney[41]和FLUX[29],均能根据文本描述生成细节丰富的图像,这标志着生成能力实现了重大飞跃。
生成图像检测
早期生成图像检测的研究主要聚焦于颜色线索[39]和饱和度线索[40]。然而,随着ProGAN[15]和扩散模型[22]的出现,这些特征在检测任务中已不再可靠。与此同时,基于频率的检测方法[28,13,58,32]也大量涌现。主流的训练型方法主要致力于训练二元分类器网络。例如,CNNspot[68]通过特定数据增强技术,成功将基于ProGAN训练的二元分类器推广到其他架构。DIRE则利用扩散模型的重构误差来训练分类器。不过,训练型方法往往受限于泛化能力不足和高昂的训练成本。为应对这些挑战,无训练方法应运而生。aeroblade通过在潜在扩散模型中使用自动编码器计算重构误差来检测生成图像,但其效果仅限于LDMs。ZED[8]采用在自然图像上预训练的无损编码器,利用编码成本差异来检测生成图像。rigid[20]利用视觉基础模型表示空间中真实图像与AI生成图像对微小噪声扰动的鲁棒性差异。
FSD
[43]从图像中提取法医显微结构,并使用高斯混合模型对真实图像的分布进行建模。基于这些前期研究成果,我们从
OOD
检测的视角重新审视生成图像检测任务,并构建了DEnD框架。该框架在理论保障下展现出卓越的泛化能力。
基于能量的 OOD
检测
分布外检测(OOD)是当前研究领域的关键方向,其核心在于识别与训练数据分布存在显著差异的样本。传统方法依赖于从softmax输出中提取置信度评分[21],但神经网络对远离训练数据的输入可能产生过高的置信度[42]。相比之下,基于能量的
OOD 检测[33]通过将输入映射为标量值——该值在分布内数据中较低、在 OOD
数据中较高——从而实现更优性能。理论层面,[12]不仅确立了 OOD
检测可学习性的必要条件,还提出了若干表征特定应用场景下 OOD
检测可学习性的充分条件。这一理论基础构成了我们方法的理论根基。
3.准备工作
本节受人类认知过程启发,将生成图像检测建模为 OOD 检测任务(参见第3.1节),并阐明本文的核心目标(参见第3.2节)。
3.1.定义
本节将详细阐述如何将生成图像检测转化为 OOD 检测任务。给定一个包含自然图像和生成图像的特征空间\({\mathcal X}\subset{\mathbb R}^d\),以及两个模式空间\({\mathcal T}_n:=\{1\}\)(表示自然图像的特征模式)和\({\mathcal T}_g:=\{2\}\)(表示生成图像的特征模式)。我们将自然图像视为ID数据,生成图像视为 OOD 数据。因此,我们得到定义在\({\mathcal X} \times {\mathcal T}_n\)上的一个ID联合分布\(D_{X_nT_n}\),其中\(X_n\in{\mathcal X}\)和\(T_n\in{\mathcal T}_n\)是随机变量。我们还定义了 OOD 联合分布\(D_{X_gT_g}\),其中\(X_g\in{\mathcal X}\)和\(T_g\in{\mathcal T}_g\)是随机变量。实证观察显示,自然图像与合成图像以任意且未知的比例混合: \[D_{X T}:=(1-\pi^{\mathrm{out}})D_{X_{n}T_{n}}+\pi^{\mathrm{out}}D_{X_{g}T_{g}},\] 其中常数 \(\pi^{\mathrm{out}}\in[0,1)\)表示未知的类别先验概率。我们只能观测到边缘分布: \[D_{X}:=(1-\pi^{\mathrm{out}})D_{X_{n}}+\pi^{\mathrm{out}}D_{X_{g}}.\] 我们将函数空间的一个子集定义为假设空间\({\mathcal H}\subset\{h:{\mathcal X}\rightarrow\{1,2\}\}\)。1代表自然图像,2代表生成图像。h称为假设函数。我们研究假设空间\({\mathcal H}\)的存在性,使得任何属于基于密度的空间 \({\mathcal D}_{HT}^{\mu,b}\)的联合分布 \(D_{XT}\)(参见附录C.2)都能满足泛化性(参见附录C.1)。
3.2.目标
我们的设计目标可表述如下:通过使用在数据集S上训练的模型f来设计检测器g,使得对于从混合边缘分布\(D_X\)中抽取的任意测试数据x,检测器能够区分输入数据是自然生成的还是合成生成的。我们定义差异能量评分 \(\lambda\)(参见第4.3节)。检测器将评分较低的数据归类为自然图像,评分较高的数据归类为合成图像。训练数据\(S:=\lbrace\mathbf{x}^{1},\ldots,\mathbf{x}^{n}\rbrace\)是从自然图像的联合分布\(D_{X_n}\)中独立同分布抽取的。
4.方法
在本节中,我们首先证明第3.1节所建模的检测器在温和假设条件下具有泛化能力(详见第4.1节)。基于理论框架,我们随后探讨了 OOD 检测的先进方法——基于能量的 OOD 检测(参见第4.2节)。然而实验表明,直接应用基于能量的 OOD 检测会导致性能欠佳。受此现象启发,并借鉴自监督学习的训练目标,我们提出了一种无需训练的泛化生成图像检测框架DEnD(详见第4.3节)。我们进一步为所提方法的泛化能力提供了理论保障(详见第4.4节),既验证了其实际有效性,又确立了理论可靠性。
4.1生成检测器的泛化能力
尽管我们已经完成了模型构建,但无法确定该检测器在何种情况下具备泛化能力。我们考虑了学习理论中的一个重要假设——可实现性假设(详见附录C.3)。该假设表明:假设空间\({\mathcal H}\)中至少存在一个模型能够完美拟合训练数据,即不存在分类错误。基于此假设,我们从 OOD 检测的可学习性[12]中推导出一个重要引理:
引理 4.1 在基于密度的空间\({\mathcal D}_{HT}^{\mu,b}\)中,若 \(\mu({\mathcal X}) < +\infin\)且满足可实现性假设,且当\({\mathcal H}\)具有有限Natarajan维度[59]时,其在\({\mathcal D}_{HT}^{\mu,b}\)中的 OOD 检测器是可学习的。
在我们的理论框架中,检测器的泛化能力与 OOD 检测的可学习性具有等价性。因此,我们推导出若干检测器泛化能力的判定条件:
- \(\mu({\mathcal X}) < +\infin\),即特征空间具有有限测度。
- 我们选择了一个合适的假设空间\({\mathcal H}\),该空间满足可实现性假设。
- 我们选择的假设空间\({\mathcal H}\)具有有限的Natarajan维度,这表明模型的复杂性得到控制,且能够很好地泛化到未见过的数据上。
4.2 基于能量的检测器
由于我们已通过理论验证,将 OOD 检测任务构建的检测器在温和假设下具有泛化能力,因此我们考虑能否直接应用OOD检测方法来有效检测生成图像。我们采用了一种先进的 OOD 检测方法:基于能量的 OOD 检测[33] (附录E中提供了关于其他 OOD 检测方法的讨论)。
我们考虑一个判别性神经分类器\(q(\mathbf{x}):\mathbb{R}^{D}\rightarrow\mathbb{R}^{K}\),该分类器将输入\(\mathbf{x}\in\mathbb{R}^{D}\)映射为logit。基于能量的 OOD 检测定义了\(\mathbf{x}\in\mathbb{R}^{D}\)上的自由能函数\(E({\bf x};q)\)为: \[E({\bf x};q)=-\tau\cdot\log\sum_{i}^{K}e^{q_i({\bf x})/\tau}.\] \(q_i({\bf x})\)表示\(q({\bf x})\)的第i个索引。温度系数\(\tau\) 被视作超参数。由于第i个标签\(q_i({\bf x})\)对应的logit可表示为\(q_{i}({\bf x})=(f({\bf x}),{\bf w}_{i})\),因此我们可以将自由能函数重新表述为: \[E({\bf x})=-\tau\cdot\log\sum_{i}^{K}e^{(f({\bf x}),{\bf w}_{i})/\tau},\] 其中\(f(\mathbf{x}):\mathbb{R}^{D}\rightarrow\mathbb{R}^{d}\)表示从输入x中提取的特征,\(\mathbf{w}_{i}\in\mathbb{R}^{d}\)表示对应第i个标签的权重。我们用(a,b)表示向量a和b的内积。文献[33]从理论上证明,采用负对数似然(NLL)损失函数训练的模型会降低分布内数据点的能量值。在实际检测过程中,能量值较高的输入自然被视为 OOD 输入,反之亦然。
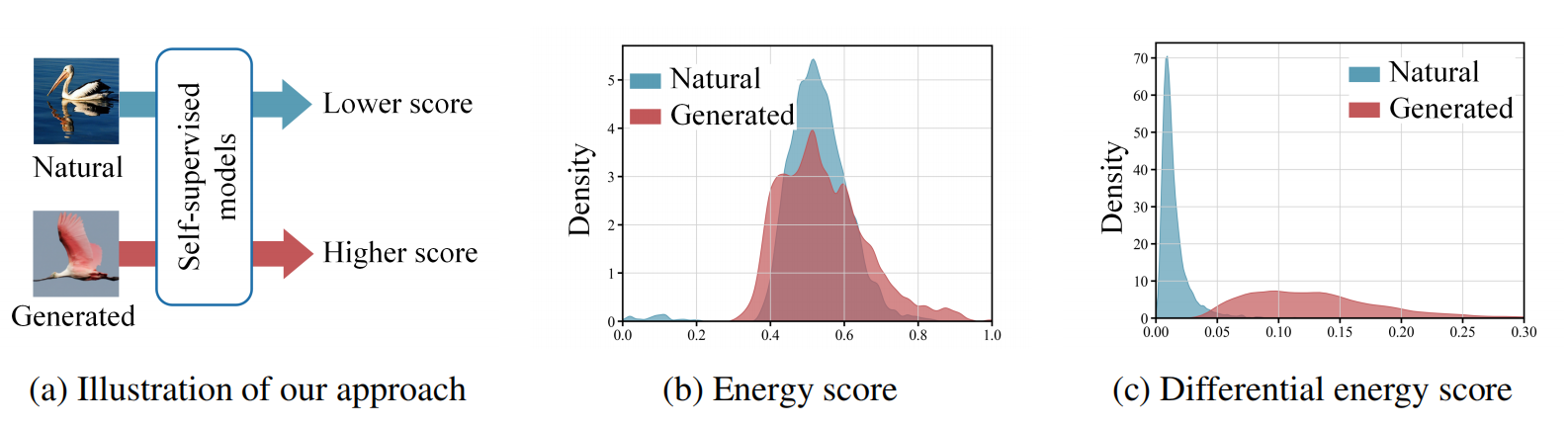
图1:(a) 我们提出基于分数的鉴别能检测(DEnD)框架用于生成图像检测,自然图像的鉴别能分数较低,反之则较高。(b) 直接采用基于能量的 OOD 检测方法进行检测效果欠佳。(c) 受自监督学习训练目标启发,我们提出通过鉴别能分数检测生成图像的方法,该方法展现出强大的泛化能力(详见附录B)。
遗憾的是,我们的实验表明自然图像与生成图像的能量分布完全无法区分(见图1b),导致检测器难以进行有效区分。这种局限性源于基于能量的OOD检测通常依赖于采用NLL损失函数训练的语义标签分类器,而自然图像与生成图像的差异主要体现在高层次模式的差异,而非简单的语义标签不匹配。为解决这一难题,我们提出用能捕捉非标签全局模式的模型替代语义标签分类器,并重新定义与模型训练目标相匹配的能量函数。
4.3 基于差异能量的检测器
如文献[61]所示,与在标签空间中运行的监督模型相比,自监督模型对全局特征表现出更高的敏感性。这一特性赋予了自监督模型潜在能力,使其能够识别生成图像与自然图像之间的模式差异。
在自监督学习[18]中,常用的方法如下:给定一个包含N个样本的批次,其特征提取器\(f(*)\)对锚点x的正样本表示为\({\bf
x}^+=m(x)\),其中m(x)表示高斯模糊等随机变换。其余N−1个样本则视为负样本。给定训练样本x,损失函数可表示为:
\[\displaystyle-\log\displaystyle\frac{e^{(f_{\theta}({\bf
x}),f_{\theta}({\bf
x}^{+}))/\tau)}}{\displaystyle\sum_{i=0}^{N}e^{(f_{\theta}({\bf
x}),f_{\theta}({\bf x}_{i}))/\tau}},\] 其中符号\({\bf x}_0={\bf
x}^+\)表示随机变换后的正样本。在自监督学习框架下,每个负样本\({\bf
x}_i\)在判别模型中对应一个独立类别。因此,负样本的特征向量\(f({\bf x}_i)\)与其所属类别的权重\(\mathbf{w}_{i}\)相对应。通过整合公式4和公式5,我们重新定义能量函数(下文所述能量函数均遵循本节所述的具体公式)如下:
\[E({\bf x};f)=\sum_{i=0}^{N}e^{(f({\bf
x}),f({\bf x}_{i}))/\tau}.\]
该总和对应一个正样本和N个负样本。在基于ID数据训练的自监督模型\(f(*)\)中,其训练目标可表示为: \[\operatorname*{min}_{\theta}{\mathbb E}_{
\mathbf{x}\sim P_{\mathrm{ID}},m\sim{\mathcal M}}E({\bf
x};f_{\theta}).\] 在我们的框架中,随机变换函数\(m(*)\)被视为一个随机变量,该变量取自定义的概率分布\({\mathcal
M}\)。该分布综合体现了对数据进行各类变换时的概率可能性。
我们从随机变换分布M中抽取k个样本点,每个样本点对应一个变换函数\(m_i(*)\)。训练目标可表示为: \[\operatorname*{min}_{\theta}\mathbb{R}_{\mathbf{x}\sim
P_{\mathrm{ID}}}\left[\frac{1}{k}\sum_{i}^{k}E_{m_{i}}(\mathbf{x};f_{\theta})\right].\]
符号\(E_{m_{i}}\)表示由随机变换\(m_i(*)\)产生的能量。
因此,对于ID分布中x的能量,对于任意
ϵ >0,我们可以推导出(完整推导过程见附录D): \[|E(\mathbf{x};f)-E(m(\mathbf{x});f)|\lt
\epsilon.\]
如图2所示,我们在ImageNet数据集[9]上进行实验,分别采用随机变换分布\({\mathcal
M}\)在1、3、5、10和15次采样。为平衡准确性和计算成本,最终选择单次采样方案。

因此,我们可以推导出:对于任意的\(\epsilon\gt 0\),任何ID数据x(即自然图像),以下结论成立: \[|E(\mathbf{x};f)-E(m(\mathbf{x});f)|\lt \epsilon\] 基于该方法,我们通过以下方式计算出差异能量评分: \[\lambda({\bf x};f,m)=|E({\bf x};f)-E(m({\bf x});f)|\,.\] 根据公式10的推导,自监督模型的训练目标可表述为最小化ID数据(自然图像)的微分能量分数。因此,对于从ID分布中抽取的x(对应自然图像),如图1c所示, \(\lambda({\bf x};f,m)\)的值相对较小。鉴于微分能量分数的判别能力,我们将其应用于生成图像检测: \[g({\bf x};\gamma,m,f)=\begin{cases}1(n a t u r a l)&\mathrm{if}\ \lambda\leq\gamma,\\2(g e n e r a t e d)&\mathrm{if}\ \lambda\gt\gamma,\\\end{cases}\] 其中\(\gamma\)为阈值(有关阈值的更多详细说明,请参见附录F),\(f\)表示预训练的自监督模型。实际应用中,我们采用强大的自监督视觉变换器(ViT)模型DINOv2(具体自监督模型选择详见附录I.2),该模型基于海量自然图像数据集完成预训练。系统通过差异能量评分进行分类:评分较高的图像被判定为生成图像,评分较低的则判定为自然图像。
4.4 DEnD的泛化性
本节在第4.1节的基础上,从理论层面构建了基于差分能量的检测(DEnD,Differential Energy-based Detection)框架,验证了该框架在生成图像检测中的泛化性。
在第4.1节中,我们指出为确保检测器的泛化能力,假设空间必须满足可实现性假设。因此,我们首先验证所提出的DEnD是否符合该假设。我们的方法设计了\({\mathcal H^*}\),其包含一个基于评分的分类器(见图1a): \[h_{\gamma}({\bf x})=\begin{cases}1&\mathrm{if}\ \lambda({\bf x};m,f)\leq\gamma,\\2&\mathrm{if}\ \lambda({\bf x};m,f)\gt\gamma,\\\end{cases}\] DEnD的设计利用了这样一个特性:在自然图像中,f函数会导致\(\lambda({\bf x};m,f)\)值相对较低,而在生成图像中则会显著升高,这种差异源于自监督模型的训练目标。该特性为以下定理奠定了理论基础:
引理4.2 若存在满足以下条件的阈值 \(\lambda^\prime\in{\mathbb R}\): \[\operatorname*{sup}_{\bf x\in s u p p D_{X_{n}}}\lambda({\bf x};f,m)\lt\gamma^{\prime}\lt\operatorname*{inf}_{\bf x\in s u p p D_{X_{g}}}\lambda({\bf x};f,m),\] 假设空间\({\mathcal H^*}\)满足可实现性假设,其中supp表示支撑集。
证明过程详见附录C.4。该定理表明,由于我们方法的判别能力,自然图像与生成图像之间的差异能量分数具有可分离性,且可实现性假设成立。这为我们的方法提供了关键的普适性保证。基于DEnD对可实现性假设的遵循,我们进一步为所提出的DEnD建立泛化性:
引理4.3 若假设空间\({\mathcal H^*}\)具有有限的Natarajan维度,则DEnD框架在 \({\mathcal D}_{HT}^{\mu,b}\)下对\({\mathcal H^*}\)具有泛化性。
证明详见附录C.5。该定理充分展现了DEnD在设计中巧妙运用微分能量评分的能力,确保了理论框架下的泛化性能。从实际应用角度看,正如第5节所述,我们的方法展现出卓越的泛化能力,与理论分析结果高度吻合。这两个方面都充分证明了我们方法的普适性。
5.实验
本节通过一系列实验,评估生成图像检测器在涉及未知生成模型的实际场景中的表现。实验结果表明,我们的方法具有显著优势(消融研究详见附录I)。
5.1.设置
数据集
我们评估了生成图像检测器在两个常用数据集上的性能:ImageNet
[9] 和 LSUN -bedroom
[74]。针对ImageNet数据集,生成图像采用了ADM[10]、ADM-G、 LDM
[56]、DiT-XL2[51]、BigGAN[2]、GigaGAN[24]、StyleGAN[26]、RQ-Transformer[30]和MaskGIT[5]等生成模型。针对
LSUN-BEDROOM数据集,我们采用ADM、 DDPM [22]、iDDPM[44]、Diffusion
Projected GAN[70]、Projected GAN[70]、StyleGAN[26]和Unleashing
Transformer[1]等生成模型生成图像。为验证本方法在未知生成模型场景下的优越性,我们在GenImage[79]和AIGCDetectBenchmark[77]两大通用基准上进行检测器评估。GenImage包含Stable
Diffusion V1.4[56]、Stable Diffusion V1.5[56]、glide[45]、 VQDM
[17]、Wukong[72]、BigGAN、ADM和Midjourney[41];AIGCDetectBenchmark[77]则涵盖ProGAN[25]、StyleGAN、BigGAN、StarGAN[7]、GauGAN[49]、StyleGAN2[27]、
WFIR [71]、ADM、glide、Midjourney、Stable Diffusion V1.4、Stable
Diffusion V1.5、 VQDM
、Wukong和DALL-E2[54]。为验证本方法对不可用生成模型的泛化能力,我们还在Sora[47]上进行了检测器评估。具体数据集来源详见附录G。
评估指标
我们沿袭先驱研究者的足迹,采用平均精度(AP,Average
Precision)和接收者操作特征曲线下面积(AUROC,Area Under the Receiver
Operating Characteristic
Curve)作为核心评估指标。在部分实验中,为确保与现有基准的可比性,我们还额外纳入准确率(ACC,accuracy)作为补充评估指标。
基线网络
我们采用基于训练和无训练两种方法作为基准。对于基于训练的方法,我们选取DIRE[69]、CNNspot[68]、UnivFD[46]、
DRCT
[6]和NPR[64]作为基准模型。部分基准模型直接采用其论文中报告的结果,包括Frank[14]、Durall[11]、Patchfor[4]、F3Net[52]、SelfBland[60]、GANDetection[38]、LGrad[65]、ResNet-50[19]、DeiTS[66]、Swin-T[35]、Spec[75]、FreDect[13]、Fusing[23]、
LNP
[32]、GenDet[78]、LaRE2[37]和GramNet[36]。对于免训练方法,我们采用aeroblade[55]和rigid[20]作为基准模型。
实验细节
在实验中,我们采用了强大的预训练自监督模型DINOv2[48]。我们选用其ViT-L/14模型,该模型以速度与性能的完美平衡著称。通过设置批量大小N=128和温度系数
τ
=0.6,我们获得了最佳性能表现(详见附录I.1)。关于m(x)的选取,我们采用均值为0、方差为0.04的高斯噪声(详见附录H)。
5.2.主要结果


与现有方法的比较
如表1和表2所示,相较于在
LSUN
-Bedroom和ImageNet数据集上基于训练的方法,我们的方法具有更强的泛化能力,在对抗大多数生成模型时表现更优,整体水平显著提升,充分展现了我们这种无需训练的通用方法的优越性。与无需训练的Aeroblade和Rigid方法相比,我们的方法在多数生成模型上展现出显著优势。虽然Rigid采用基于经验观察的噪声方法,但我们的方法源自自监督模型的训练目标。这种基础性视角使我们设计出更有效的差异能量评分机制,从而获得更优性能。


如表3和表5所示,面对更先进复杂的生成模型时,基于训练的方法通常在处理训练过程中未见过的生成模型时表现欠佳。相比之下,我们的方法具有出色的泛化能力,性能显著优于现有基于训练的方法。然而,由于预训练模型表征能力的局限,当处理某些高保真图像(尤其是来自Stable Diffusion的图像)时,我们的方法会出现性能下降。我们认为,采用表征能力更强的模型可以缓解这一局限。
关于泛化能力的讨论
我们的方法在泛化性能方面展现出显著提升。从训练角度而言,传统基于训练的方法常面临过拟合问题。如表5所示,基于ProGAN训练的模型仅在其他GAN生成样本上表现良好。相比之下,我们的免训练方法天生规避过拟合风险。从理论层面看,由于不同生成架构的多样性,生成图像的模式可能千差万别。这种复杂性给基于训练的方法带来重大挑战。而我们的方法将所有生成图像的模式视为
OOD
数据,从而在各类生成模型间保持强大的泛化能力。此外,我们的方法还提供了泛化性的理论保障,这是现有方法所不具备的独特优势。
在Sora上的评估
Sora等视频生成模型的架构往往未知,这使得检测这类新型未知模型更具挑战性。

如表4所示,我们在Sora上的实验表明,我们的方法具有强大的泛化能力,即使在未知架构的生成模型上测试,仍能取得具有竞争力的性能——这是现有方法所不具备的关键优势。
5.3.鲁棒性评估
在实际应用中,检测器经常需要处理质量下降的图像。例如,有损压缩可能产生伪影,而通信信道传输过程中通常会产生噪声。基于先前研究[55],我们评估了检测器在JPEG压缩、高斯噪声和高斯模糊等常见场景下的鲁棒性。这些实验均在ImageNet数据集上完成。

图3:检测器在处理退化图像时的性能表现。(a):JPEG格式图像,质量参数q。(b):高斯噪声,标准差 \(\sigma\) 。(c):高斯模糊,标准差 \(\sigma\) 。
如图3所示,深度神经网络(Deep Neural Network,DEnD)在各类图像退化场景中均展现出卓越性能,充分体现了其强大的鲁棒性。相比之下,其他基于训练的方法往往表现欠佳。这种优势源于我们方法的内在泛化能力——该能力建立在坚实的理论基础之上,使其能够始终如一地将退化的ID数据(自然图像)分类为ID数据(自然图像)。
6.限制
1) 本研究将生成图像检测问题转化为 OOD 检测任务,并基于能量型 OOD 检测方法提出创新框架。虽然当前方案以能量型 OOD 检测为核心,但我们明确承认其他先进 OOD 检测策略的可行性。后续研究将重点探索其他 OOD 检测策略的适用性。2) 实验结果表明,我们的方法凭借理论保障展现出卓越性能。然而受限于训练集规模,预训练模型在面对真实数据分布偏移时(详见附录J),往往难以充分发挥框架潜力。未来我们将通过微调模型来提升泛化能力。
7.结论
本文从人类认知辨别生成图像的能力中获得启发,提出了一种全新的生成图像检测理解与改进视角:将其建模为 OOD 检测任务。基于此,我们阐明了完全基于自然图像训练的模型在生成图像检测中的可行性。为实现这一洞见,我们引入了基于微分能量的检测(DEnD)框架——一种无需训练且具有普适性的生成图像检测方法。大量实验表明,我们的方法在常见基准测试中表现优异。此外,该方法展现出卓越的泛化能力,能有效处理架构未知的生成模型(如Sora)。更广泛地说,我们的研究不仅在理论上有所贡献,还提供了一种兼具高效性和泛化能力的生成图像检测方法,为应对日益严峻的图像伪造危机提供了解决方案。
